میانه چیست ? (Median) و چگونه آن را محاسبه کنیم، با مثال
چکیده مقاله :
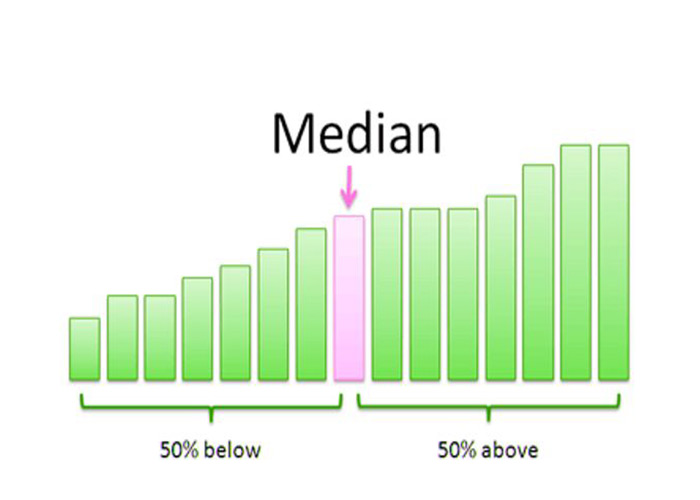
در آمار، میانه معیاری از تمایل مرکزی است که یک مجموعه داده را به دو قسمت مساوی تقسیم می کند. مقداری است که نیمه بالایی یک مجموعه داده را از نیمه پایینی جدا می کند وقتی داده ها به ترتیب بزرگی مرتب شوند. برای یافتن میانه، ابتدا داده ها باید از کمترین به بالاترین (یا بالاترین به پایین ترین) مرتب شوند. اگر مجموعه داده دارای تعداد مشاهدات فرد باشد، میانه مقدار وسط است. اگر مجموعه داده دارای تعداد مشاهدات زوج باشد، میانه میانگین دو مقدار میانی است. میانه یک آمار قوی است، به این معنی که تحت تأثیر مقادیر شدید (پرت) در مجموعه داده قرار نمی گیرد. اغلب در موقعیتهایی استفاده میشود که میانگین (یکی دیگر از معیارهای گرایش مرکزی) به دلیل وجود نقاط پرت یا توزیعهای اریب مناسب نیست. میانه همچنین هنگام توصیف داده های ترتیبی مفید است، جایی که ترتیب مقادیر مهم است، اما مقادیر عددی دقیق کمتر هستند. در این مقاله می خواهیم بدانیم که به طور دقیق میانه چیست ؟ با ذکر مثال و تعریف مفهوم و کاربرد آن در تحلیل آماری .
1- میانه چیست؟
Median یا میانه عدد میانی در فهرست مرتب شده، صعودی یا نزولی از اعداد است و می تواند بیشتر از میانگین آن مجموعه داده را توصیف کند. این نقطه ای است که در بالا و پایین آن نیمی (50%) از داده های مشاهده شده قرار می گیرد و بنابراین نشان دهنده نقطه میانی داده ها است.
میانه اغلب با سایر آمارهای توصیفی مانند میانگین (میانگین)، مد و انحراف معیار مقایسه می شود.
نکات کلیدی
- میانه عدد میانی در لیست مرتب شده اعداد است و می تواند بیشتر از میانگین آن مجموعه داده را توصیف کند.
- میانه گاهی اوقات بر خلاف میانگین استفاده می شود، زمانی که نقاط پرت در دنباله وجود دارد که ممکن است میانگین مقادیر را منحرف کند.
- اگر تعداد اعداد فرد وجود داشته باشد، مقدار میانه عددی است که در وسط قرار دارد، با همان تعداد اعداد زیر و بالاتر.
- اگر تعداد زوجی از اعداد در لیست وجود داشته باشد، برای یافتن مقدار میانه، باید جفت وسط تعیین شود، با هم جمع شوند و بر دو تقسیم شوند.
- در توزیع نرمال، میانه همان میانگین و مد است.
جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تحلیل آماری چیست مطالعه نمایید.
2- تعریف میانه یا Median
همانطورکه گفته شد، میانه معیاری از تمایل مرکزی است که به طور گسترده برای توصیف مرکز یک مجموعه داده استفاده می شود. زمانی که داده ها به ترتیب صعودی مرتب شوند، به عنوان مقداری تعریف می شود که نیمه بالایی یک مجموعه داده را از نیمه پایینی جدا می کند. برای یافتن میانه، ابتدا داده ها باید از کمترین به بالاترین (یا بالاترین به پایین ترین) مرتب شوند.
یکی از مزایای میانه نسبت به سایر معیارهای گرایش مرکزی، مانند میانگین یا مد، مقاومت آن در برابر نقاط پرت است. نقاط پرت نقاط داده ای هستند که به طور قابل توجهی با بقیه مجموعه داده ها متفاوت هستند و می توانند بر میانگین داده ها تأثیر زیادی بگذارند. با این حال، میانه تحت تأثیر مقادیر پرت قرار نمی گیرد زیرا فقط موقعیت مقادیر در مجموعه داده را در نظر می گیرد، نه مقادیر عددی آنها. این میانه را به ابزار مفیدی برای توصیف مجموعه دادهها با مقادیر شدید یا توزیعهای اریب تبدیل میکند.
میانه همچنین برای توصیف داده های ترتیبی مفید است، داده هایی که می توانند مرتب شوند اما مقدار عددی ندارند. به عنوان مثال، ترتیب نهایی کننده ها در یک مسابقه را می توان با استفاده از میانه توصیف کرد، حتی اگر زمان دقیق پایان بازی مهم نباشد. به طور مشابه، میانه می تواند برای توصیف رتبه بندی ترجیحات در یک نظرسنجی استفاده شود، که در آن از پاسخ دهندگان خواسته می شود ترجیحات خود را به ترتیب خاصی رتبه بندی کنند.
در برخی موارد، میانه ممکن است معیار خوبی برای گرایش مرکزی نباشد. به عنوان مثال، اگر مجموعه داده دارای یک توزیع دووجهی باشد، که در آن دو قله مجزا در داده ها وجود داشته باشد، میانه ممکن است به طور دقیق مرکز داده ها را نشان ندهد. در چنین مواردی، سایر معیارهای گرایش مرکزی، مانند میانگین یا حالت، ممکن است مناسب تر باشند.
میانه اغلب همراه با سایر معیارهای تغییرپذیری، مانند محدوده یا Interquartile Range (IQR)، برای توصیف گسترش داده ها استفاده می شود. Range تفاوت بین حداکثر و حداقل مقادیر در مجموعه داده است، در حالی که IQR تفاوت بین 75 و 25 درصد داده ها است. IQR یک معیار مفید برای تغییرپذیری است زیرا تحت تأثیر عوامل پرت، مشابه میانه قرار نمی گیرد.
مجدد اعلام می کنیم که میانه عدد میانی در لیست مرتب شده اعداد است. برای تعیین مقدار میانه در دنباله ای از اعداد، ابتدا باید اعداد را به ترتیب ارزش از کمترین به بالاترین یا بالاترین به کمترین مرتب کنیم. میانه را می توان برای تعیین میانگین تقریبی یا میانگین استفاده کرد، اما نباید با میانگین واقعی اشتباه گرفته شود.
- اگر تعداد اعداد فرد وجود داشته باشد، مقدار میانه عددی است که در وسط قرار دارد، با همان تعداد اعداد زیر و بالاتر.
- اگر تعداد زوجی از اعداد در لیست وجود داشته باشد، برای یافتن مقدار میانه، باید جفت وسط تعیین شود، با هم جمع شوند و بر دو تقسیم شوند.
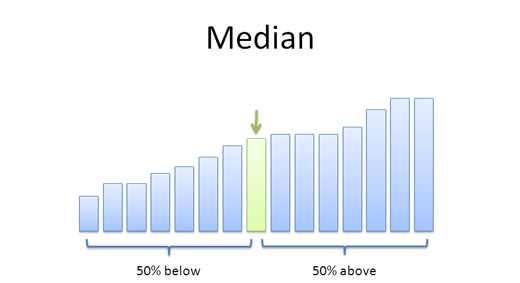
میانه گاهی اوقات بر خلاف میانگین استفاده می شود، زمانی که نقاط پرت در دنباله وجود دارد که ممکن است میانگین مقادیر را منحرف کند. میانه یک دنباله کمتر از میانگین تحت تأثیر عوامل پرت قرار می گیرد.
3- مثال میانه
برای یافتن مقدار میانه در لیستی با تعداد فرد از اعداد، می توان عددی را که در وسط قرار دارد با تعداد مساوی از اعداد در دو طرف میانه پیدا کرد. برای یافتن میانه، ابتدا اعداد را به ترتیب مرتب کنید، معمولاً از کمترین به بالاترین.
به عنوان مثال، در مجموعه داده های ، ترتیب مرتب شده به تبدیل می شود. میانه عددی است که در وسط قرار دارد، که در این مورد 13 است زیرا سه عدد در هر طرف وجود دارد.
برای یافتن مقدار میانه در یک لیست با تعداد زوج، باید جفت وسط را تعیین کرد، آنها را جمع کرد و بر دو تقسیم کرد. مجدداً اعداد را به ترتیب از کمترین به بالاترین مرتب کنید.
به عنوان مثال، در مجموعه داده های ، ترتیب مرتب شده به تبدیل می شود. میانه میانگین دو عدد در وسط است که در این حالت پانزده است .
نکته: میانه ارتباط نزدیکی با چارک ها یا تقسیم داده های مشاهده شده به چهار قسمت مساوی دارد. میانه نقطه مرکزی خواهد بود که دو ربع اول در زیر آن و دو ربع دوم بالای آن قرار می گیرند. روش های دیگر Bucketing Data شامل پنجک (در پنج بخش) و دهک ها (در 10 بخش) است.
4- چگونه میانه را محاسبه کنیم؟
میانه مقدار وسط در مجموعه ای از داده ها است. ابتدا داده ها را از کوچکترین به بزرگتر سازماندهی و مرتب کنید. برای یافتن مقدار میانی، تعداد مشاهدات را بر دو تقسیم کنید. اگر تعداد مشاهدات فرد وجود دارد، آن عدد را به سمت بالا گرد کنید، و مقدار در آن موقعیت، میانه است. اگر تعداد مشاهدات زوج است، میانگین مقادیر موجود در بالا و پایین آن موقعیت را بگیرید.
5- سوالات پرتکرار
1-5- میانه در یک توزیع نرمال کجاست؟
در توزیع نرمال ("منحنی زنگ") میانه، میانگین و مد همگی یک مقدار هستند و در بالاترین نقطه در مرکز منحنی قرار می گیرند.
2-5- چه زمانی میانگین و میانه متفاوت است؟
در یک مجموعه داده غیر متوازن، میانگین و میانه معمولاً متفاوت خواهد بود. میانگین با جمع کردن تمام مقادیر موجود در داده ها و تقسیم بر تعداد مشاهدات محاسبه می شود. اگر مقادیر پرت قابل توجهی وجود داشته باشد، یا اگر داده ها حول مقادیر خاصی جمع شوند، میانگین (میانگین) نقطه میانی داده نخواهد بود.
به عنوان مثال، در مجموعه ای از داده ها میانگین 24/8 = 3 خواهد بود. با این حال، میانه، 1 (مقدار نقطه میانی) خواهد بود.
به همین دلیل است که بسیاری از اقتصاددانان میانه را برای گزارش درآمد یا ثروت یک کشور ترجیح می دهند، زیرا بیشتر نماینده توزیع درآمد واقعی است.
نتیجه گیری:
به طور خلاصه، میانه ابزار مفیدی در آمار برای توصیف مرکز یک مجموعه داده است، به خصوص زمانی که میانگین به دلیل وجود نقاط پرت یا توزیع های اریب، نمایش خوبی از داده ها نباشد. این یک معیار قوی از تمایل مرکزی است که تحت تأثیر مقادیر شدید در مجموعه داده قرار نمی گیرد. میانه همچنین برای توصیف داده های ترتیبی مفید است، جایی که ترتیب مقادیر مهم است اما مقادیر عددی دقیق کمتر هستند. جهت کسب اطلاعات بیشتر و پیشبرد پروژه خود می توانید از مشاوره آماری لنسرسرا بهره مند شوید.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











