بهینه کردن portfolio با توزیع نرمال

چکیده مقاله :
هنگام بهینه سازی پورتفولیوی خود، یک “وزن بهینه سازی” برای هر طبقه دارایی و همه دارایی های آن طبقه اختصاص می دهید. وزن درصدی از پرتفوی است که در هر طبقه خاص متمرکز شده است. به عنوان مثال، فرض کنید ما سهام را 10٪ و اوراق قرضه را 20٪ وزن می کنیم. در این مقاله می خواهیم بهینه کردن portfolio با توزیع نرمال را توضیح دهیم.

1- معرفی 7 تکنیک تحلیل آماری

توزیع نرمال، توزیع احتمالی است که تمام مقادیر آن را در امتداد یک منحنی زنگی متقارن ترسیم می‌کند، با بیشترین احتمالات که حول مقدار میانگین متمرکز شده و به سمت دم‌ها کاهش می‌یابد. توزیع نرمال یک مفهوم کلیدی در آمار و سرمایه گذاری است. بسیاری از مدل های مالی فرض می کنند که بازده سرمایه گذاری برای یک دارایی معین از توزیع نرمال پیروی می کند.

مفاهیم کلیدی

• توزیع نرمال، توزیع احتمالی است که از نمودار یک منحنی زنگی پیروی می‌کند: رایج‌ترین نتایج حول میانگین خوشه‌بندی می‌شوند و احتمال به سمت دنباله‌ها کاهش می‌یابد.
• توزیع نرمال با مقدار میانگین و انحراف استاندارد تعیین می شود که نشان دهنده گسترش مقادیر است.
• توزیع نرمال یک عنصر کلیدی برای تئوری مدرن پرتفولیو است، یک رویکرد ریاضی برای سرمایه گذاری که فرض می کند بازده معینی از توزیع نرمال پیروی می کند.

جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تحلیل آماری چیست مطالعه نمایید.

• تحلیل آماری چیست ؟

2- توزیع نرمال (منحنی زنگ)

مجموعه داده ها (مانند قد 100 انسان، نمرات به دست آمده توسط 45 دانش آموز در یک کلاس، و غیره) تمایل دارند مقادیر زیادی در یک نقطه داده یا در محدوده مشابه داشته باشند. این توزیع نقاط داده را توزیع منحنی معمولی یا زنگی می نامند.

برای مثال، در یک گروه 100 نفره، 10 نفر ممکن است کمتر از 5 فوت قد داشته باشند، 65 نفر ممکن است بین 5 تا 5.5 فوت باشند و 25 نفر ممکن است بالای 5.5 فوت باشند. این توزیع محدود به محدوده را می توان به صورت زیر ترسیم کرد:

• توزیع متقارن چیست؟

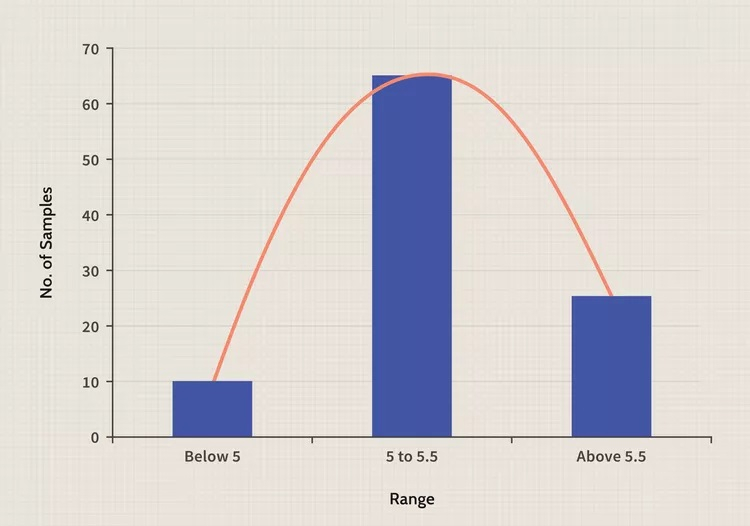
به طور مشابه، نقاط داده ترسیم شده در نمودارها برای هر مجموعه داده معین ممکن است شبیه انواع مختلف توزیع باشد. سه مورد از رایج‌ترین آنها توزیع‌های تراز چپ، تراز راست و درهم ریخته هستند:

• توزیع نامتقارن چیست؟

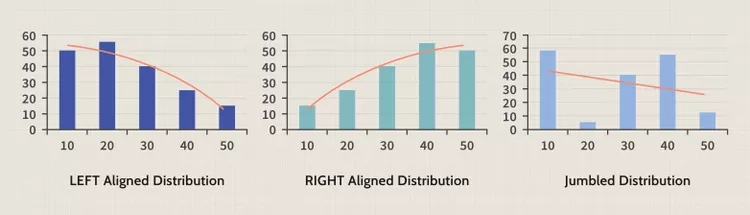
به خط روند قرمز در هر یک از این نمودارها توجه کنید. این تقریباً روند توزیع داده ها را نشان می دهد. اولین، “توزیع تراز چپ”، نشان می دهد که اکثر نقاط داده در محدوده پایین تر قرار می گیرند. در نمودار دوم “توزیع تراز شده راست”، اکثر نقاط داده در انتهای بالاتر محدوده قرار می گیرند، در حالی که آخرین، “توزیع درهم”، مجموعه داده های مختلط را بدون هیچ روند واضحی نشان می دهد.

موارد زیادی وجود دارد که در آن توزیع نقاط داده حول یک مقدار مرکزی است، و این نمودار یک توزیع نرمال کامل را نشان می دهد – به طور مساوی در هر دو طرف متعادل است، با بیشترین تعداد نقاط داده در مرکز متمرکز شده است.

در اینجا یک مجموعه داده کامل و به طور معمول توزیع شده است:

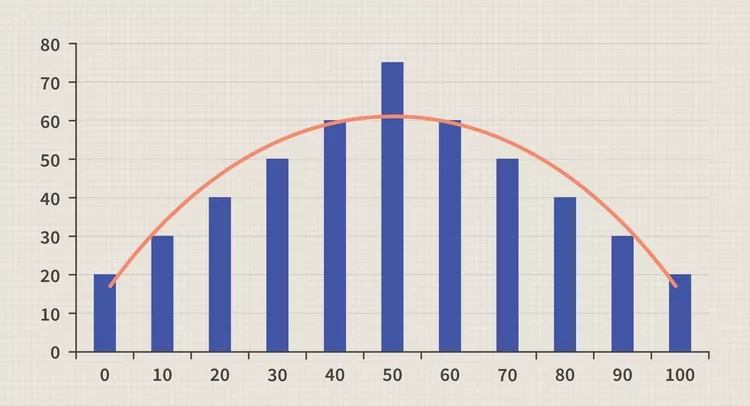
مقدار مرکزی در اینجا 50 است (که دارای بیشترین تعداد نقاط داده است) و توزیع به طور یکنواخت به سمت مقادیر انتهایی 0 و 100 (که کمترین تعداد نقاط داده را دارند) کاهش می یابد. توزیع نرمال به صورت متقارن حول مقدار مرکزی با نصف مقادیر در هر طرف است.

بسیاری از مثال‌های واقعی با توزیع منحنی زنگی مطابقت دارند:

• یک سکه منصفانه را بارها پرتاب کنید (مثلاً 10 بار یا بیشتر) و می توانید انتظار داشته باشید که حدود نیمی از نتایج سرها باشد. آزمایش را 1000 بار تکرار کنید و نتیجه از توزیع طبیعی پیروی خواهد کرد: رایج ترین نتیجه 4-6 سر خواهد بود، در حالی که بسیار نادر است که همه سرها یا همه دم ها را برگردانید.
• یک جفت تاس منصفانه را چندین بار پرتاب کنید (مثلاً 100 بار یا بیشتر) و نتیجه یک توزیع متعادل و نرمال در مرکز عدد 7 خواهد بود و به طور یکنواخت به سمت مقادیر انتهایی 2 و 12 کاهش می یابد.
• قد افراد در یک گروه با اندازه قابل توجه و نمرات به دست آمده توسط افراد در یک طبقه، هر دو از الگوهای توزیع نرمال پیروی می کنند.
• در امور مالی، تغییرات در مقادیر ثبت نرخ‌های فارکس، شاخص‌های قیمت و قیمت سهام به‌طور معمول توزیع می‌شوند.

• چولگی چیست؟

• کشیدگی در آمار چیست؟

3- ریسک و بازده

هر سرمایه گذاری دو جنبه دارد: ریسک و بازده. سرمایه گذاران به دنبال کمترین ریسک ممکن برای بالاترین بازده هستند. توزیع نرمال این دو جنبه را با میانگین بازده و انحراف استاندارد برای ریسک کمیت می کند.

مقدار متوسط یا مورد انتظار

یک تغییر میانگین خاص در قیمت یک سهم می تواند 1.5٪ به صورت روزانه باشد، به این معنی که به طور متوسط 1.5٪ افزایش می یابد. این مقدار متوسط یا ارزش مورد انتظار نشان دهنده بازده را می توان با محاسبه میانگین در یک مجموعه داده به اندازه کافی بزرگ که حاوی تغییرات قیمت روزانه تاریخی آن سهام است به دست آورد. هر چه میانگین بالاتر باشد بهتر است.

انحراف معیار

انحراف استاندارد مقداری را نشان می دهد که مقادیر به طور متوسط از میانگین انحراف دارند. هر چه انحراف استاندارد بیشتر باشد، سرمایه گذاری ریسک بیشتری دارد، زیرا منجر به عدم اطمینان بیشتر می شود.

• انحراف استاندارد چیست؟

در اینجا یک نمایش گرافیکی از انحراف معیار ارائه شده است:

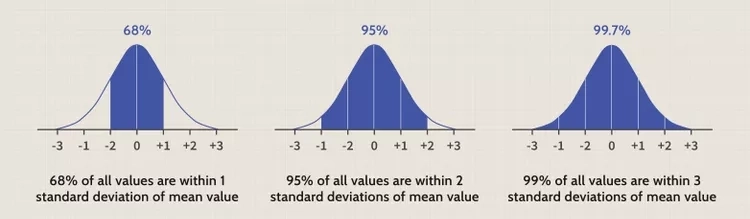
از این رو، نمایش گرافیکی توزیع نرمال از طریق میانگین و انحراف استاندارد آن، نمایش هر دو بازده و ریسک را در یک محدوده به وضوح تعریف شده امکان پذیر می کند.

این کمک می کند که بدانیم (و با اطمینان مطمئن باشیم) که اگر برخی از مجموعه داده ها از الگوی توزیع نرمال پیروی کنند، میانگین آن به ما امکان می دهد بدانیم چه بازدهی را انتظار داریم، و انحراف استاندارد آن ما را قادر می سازد که بدانیم حدود 68٪ از مقادیر در 1 انحراف استاندارد، 95٪ در 2 انحراف استاندارد و 99٪ مقادیر در 3 انحراف استاندارد قرار می گیرند. مجموعه داده ای که میانگین 1.5 و انحراف استاندارد 1 دارد، بسیار پرخطرتر از مجموعه داده دیگری با میانگین 1.5 و انحراف استاندارد 0.1 است.

دانستن این مقادیر برای هر دارایی انتخاب شده (یعنی سهام، اوراق قرضه و وجوه) سرمایه گذار را از بازده و خطرات مورد انتظار آگاه می کند.

به کارگیری این مفهوم و نشان دادن ریسک و بازده در یک سهام، اوراق قرضه یا صندوق، آسان است. اما آیا می توان این را به مجموعه ای از دارایی های متعدد تعمیم داد؟

افراد تجارت را با خرید یک سهام یا اوراق قرضه یا سرمایه گذاری در یک صندوق سرمایه گذاری آغاز می کنند. به تدریج، آنها تمایل دارند دارایی های خود را افزایش دهند و چندین سهام، وجوه یا دارایی های دیگر را خریداری کنند و در نتیجه سبد سهام ایجاد کنند. در این سناریوی افزایشی، افراد بدون داشتن استراتژی و یا پیش بینی زیاد، پورتفولیوهای خود را می سازند. مدیران حرفه ای صندوق، معامله گران و بازارسازان از روشی سیستماتیک برای ایجاد سبد سهام خود با استفاده از یک رویکرد ریاضی به نام نظریه پورتفولیو مدرن (MPT) پیروی می کنند که بر اساس مفهوم “توزیع عادی” بنا شده است.

4- تئوری پورتفولیو مدرن

نظریه پورتفولیو مدرن (MPT) یک رویکرد ریاضی سیستماتیک را ارائه می دهد که هدف آن به حداکثر رساندن بازده مورد انتظار یک سبد برای مقدار معینی از ریسک پرتفوی با انتخاب نسبت دارایی های مختلف است. متناوبا، همچنین پیشنهاد می‌کند تا ریسک را برای سطح معینی از بازده مورد انتظار به حداقل برساند.

برای دستیابی به این هدف، دارایی هایی که باید در پرتفوی گنجانده شوند، نباید صرفاً بر اساس شایستگی فردی خود انتخاب شوند، بلکه باید بر اساس نحوه عملکرد هر دارایی نسبت به سایر دارایی های موجود در پرتفوی انتخاب شوند.

به طور خلاصه، MPT چگونگی دستیابی به تنوع پرتفوی را برای بهترین نتایج ممکن تعریف می کند: حداکثر بازده برای سطح قابل قبول ریسک یا حداقل ریسک برای سطح بازده مطلوب.

5- The Building Blocks

MPT زمانی که معرفی شد آنقدر مفهوم انقلابی بود که مخترعان آن برنده جایزه نوبل شدند. این نظریه با موفقیت یک فرمول ریاضی را برای هدایت تنوع در سرمایه گذاری ارائه کرد.

تنوع بخشی یک تکنیک مدیریت ریسک است که ریسک «همه تخم‌ها در یک سبد» را با سرمایه‌گذاری در سهام، بخش‌ها یا طبقات دارایی غیرهمبسته حذف می‌کند. در حالت ایده آل، عملکرد مثبت یک دارایی در پرتفوی، عملکرد منفی سایر دارایی ها را خنثی می کند.

برای در نظر گرفتن میانگین بازده پرتفویی که دارای n دارایی متفاوت است، ترکیب وزنی نسبت بازده دارایی های تشکیل دهنده محاسبه می شود.

با توجه به ماهیت محاسبات آماری و توزیع نرمال، بازده کل پرتفوی (Rp) به صورت زیر محاسبه می شود:

مجموع (∑)، جایی که wi وزن متناسب دارایی i در پرتفوی است، Ri بازده (میانگین) دارایی i است.

ریسک پرتفوی (یا انحراف استاندارد) تابعی از همبستگی‌های دارایی‌های مشمول، برای همه جفت‌های دارایی (با توجه به یکدیگر در جفت) است.

با توجه به ماهیت محاسبات آماری و توزیع نرمال، ریسک کلی پرتفوی (Std-dev)p به صورت زیر محاسبه می شود:

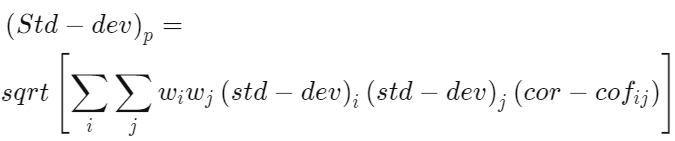
در اینجا، cor-cof ضریب همبستگی بین بازده دارایی‌های i و j است و sqrt ریشه مربع است.

این به عملکرد نسبی هر دارایی نسبت به دیگری توجه می کند.

اگرچه این از نظر ریاضی پیچیده به نظر می رسد، مفهوم ساده به کار رفته در اینجا نه تنها شامل انحرافات استاندارد دارایی های فردی، بلکه دارایی های مرتبط با یکدیگر نیز می شود.

یک مثال خوب در اینجا از دانشگاه واشنگتن موجود است.

6- یک مثال از MPT

به عنوان یک آزمایش فکری، بیایید تصور کنیم یک مدیر پورتفولیو هستیم که به او سرمایه داده شده است و وظیفه داریم که چقدر سرمایه باید به دو دارایی موجود (A & B) تخصیص داده شود تا بازده مورد انتظار به حداکثر برسد و ریسک کاهش یابد.

ما همچنین مقادیر زیر را در دسترس داریم:

Ra = 0.175

Rb = 0.055

(Std-dev)a = 0.258

(Std-dev)b = 0.115

(Std-dev)ab = -0.004875

(Cor-cof)ab = -0.164

با تخصیص مساوی 50-50 به هر دارایی A و B، Rp به 0.115 و (Std-dev)p به 0.1323 می رسد. یک مقایسه ساده به ما می گوید که برای این 2 سبد دارایی، بازده و ریسک در میانه راه بین ارزش های فردی هر دارایی است.

با این حال، هدف ما بهبود بازده پرتفوی فراتر از میانگین صرف هر یک از دارایی ها و کاهش ریسک است، به طوری که از دارایی های فردی کمتر باشد.

حال بیایید موقعیت تخصیص سرمایه 1.5 در دارایی A و موقعیت تخصیص سرمایه 0.5- در دارایی B را در نظر بگیریم. به عبارت دیگر، ما سهام B را برای 0.5 برابر سرمایه کوتاه می کنیم و از آن پول برای خرید سهام A به مبلغ 1.5 برابر سرمایه استفاده می کنیم.)

با استفاده از این مقادیر، Rp را به عنوان 0.1604 و (Std-dev)p را به عنوان 0.4005 دریافت می کنیم.

به طور مشابه، می‌توانیم به استفاده از وزن‌های تخصیص مختلف برای دارایی‌های A و B ادامه دهیم و به مجموعه‌های مختلف Rp و (Std-dev)p برسیم. با توجه به بازده مورد نظر (Rp)، می توان قابل قبول ترین سطح ریسک (std-dev)p را انتخاب کرد. به طور متناوب، برای سطح ریسک مورد نظر، می توان بهترین بازده پرتفوی موجود را انتخاب کرد. در هر صورت، از طریق این مدل ریاضی تئوری پورتفولیو، می توان به هدف ایجاد یک پرتفوی کارآمد با ترکیب ریسک و بازده مورد نظر دست یافت.

استفاده از ابزارهای خودکار به شما این امکان را می دهد که به راحتی و بدون نیاز به محاسبات دستی طولانی، بهترین نسبت های تخصیص یافته ممکن را به راحتی تشخیص دهید.

مرز کارآمد، مدل قیمت‌گذاری دارایی سرمایه (CAPM) و قیمت‌گذاری دارایی با استفاده از MPT نیز از همان مدل توزیع معمولی تکامل یافته و توسعه‌ای برای MPT است.

7- چالش‌های MPT (و توزیع عادی اساسی)

متأسفانه هیچ مدل ریاضی کاملی نیست و هر کدام دارای نارسایی ها و محدودیت هایی هستند.

این فرض اساسی که بازده قیمت سهام از توزیع نرمال پیروی می کند بارها و بارها مورد تردید قرار می گیرد. شواهد تجربی کافی برای مواردی وجود دارد که مقادیر به توزیع نرمال فرضی پایبند نیستند. مبنا کردن مدل‌های پیچیده بر روی چنین مفروضاتی ممکن است به نتایجی با انحرافات بزرگ منجر شود.

با رفتن بیشتر به MPT، محاسبات و مفروضات مربوط به ثابت ماندن ضریب همبستگی و کوواریانس (بر اساس داده های تاریخی) ممکن است لزوماً برای مقادیر مورد انتظار آینده صادق نباشند. به عنوان مثال، بازارهای اوراق قرضه و سهام یک همبستگی کامل را در بازار بریتانیا از دوره 2001 تا 2004 نشان دادند، جایی که بازده هر دو دارایی به طور همزمان کاهش یافت. در واقع، برعکس در دوره های تاریخی طولانی قبل از سال 2001 مشاهده شده است.

رفتار سرمایه گذار در این مدل ریاضی در نظر گرفته نمی شود. مالیات ها و هزینه های مبادله نادیده گرفته می شود، حتی اگر تخصیص سرمایه کسری دارایی ها را فرض می کند.

در واقع، هیچ یک از این مفروضات ممکن است درست نباشد، به این معنی که بازده مالی تحقق یافته ممکن است به طور قابل توجهی با سود مورد انتظار متفاوت باشد.

8- چگونه از آمار در سرمایه گذاری استفاده می شود؟

تحلیلگران از ابزارهای آماری برای تخمین بازده احتمالی پرتفوی های سهام خاص یا بازده بازار گسترده تر استفاده می کنند. در تحلیل تکنیکال، آنها همچنین ممکن است از شاخص های ترند برای پیش بینی رفتار سایر فعالان بازار استفاده کنند.

9- تحلیلگران در بورس به دنبال چه آماری هستند؟

تعداد انگشت شماری از معیارهای کلیدی وجود دارد که تحلیلگران برای ارزیابی عملکرد سهام از آنها استفاده می کنند. ارقامی مانند نسبت قیمت به درآمد، نسبت بدهی به حقوق صاحبان سهام، جریان نقدی آزاد و نسبت PEG برای ارزیابی سودآوری شرکت‌های دولتی مختلف استفاده می‌شوند.

10- انحراف معیار چه کاری انجام می دهد؟

انحراف استاندارد یک اندازه گیری آماری برای “گسترش” یک مجموعه داده خاص است. انحراف استاندارد پایین نشان می‌دهد که مقادیر نزدیک به میانگین جمع شده‌اند، در حالی که انحراف استاندارد بالا نشان می‌دهد که آنها پراکنده‌تر هستند. برای توزیع کاملاً نرمال، 68 درصد پیامدها در یک انحراف معیار از میانگین و 95 درصد در دو انحراف معیار قرار خواهند گرفت.

نتیجه گیری

مدل‌های ریاضی مکانیسم خوبی برای تعیین کمیت برخی متغیرها با اعداد منفرد و قابل ردیابی فراهم می‌کنند. اما به دلیل محدودیت‌های مفروضات، مدل‌ها ممکن است شکست بخورند.

توزیع نرمال، که اساس تئوری پرتفوی را تشکیل می دهد، ممکن است لزوماً در مورد سهام و سایر الگوهای قیمت دارایی مالی اعمال نشود. نظریه پورتفولیو به خودی خود دارای مفروضات زیادی است که باید قبل از اتخاذ تصمیمات مالی مهم به طور انتقادی مورد بررسی قرار گیرند.