تابع توزیع تجمعی چیست؟

چکیده مقاله :
در احتمالات و آمار، تابع توزیع تجمعی (CDF) یک متغیر تصادفی با ارزش واقعی، مثلاً «X» که با x ارزیابی میشود، احتمال این است که X مقداری کمتر یا مساوی با x بگیرد. متغیر تصادفی متغیری است که مقادیر احتمالی نتیجه یک پدیده غیرمنتظره را تعریف می کند. هم برای متغیرهای گسسته و هم برای متغیرهای تصادفی تعریف شده است. همچنین برای تعیین توزیع متغیرهای تصادفی چند متغیره استفاده می شود. اگر متغیر تصادفی بالاتر از یک سطح خاص باشد، به آن توزیع دم یا تابع توزیع تجمعی تکمیلی (CCDF) میگویند. در این مقاله متوجه خواهید شد که تابع توزیع تجمعی چیست، خواص، فرمول ها، کاربردها و مثال های آن را نیز ارائه کرده ایم.
1- تابع توزیع تجمعی چیست؟
تابع توزیع تجمعی (CDF) به ازای یک متغیر تصادفی با ارزش واقعی X، که در x ارزیابی میشود، تابع احتمالی است که در آن X مقداری کمتر یا مساوی با x میگیرد. برای توصیف توزیع احتمال متغیرهای تصادفی در یک جدول استفاده می شود و با کمک این داده ها می توانیم به راحتی یک نمودار CDF در یک برگه اکسل ایجاد کنیم.
به عبارت دیگر، CDF احتمال تجمعی را برای مقدار داده شده پیدا می کند. برای تعیین احتمال یک متغیر تصادفی از آن و همچنین برای مقایسه احتمال بین مقادیر در شرایط خاص استفاده می شود. برای توابع توزیع گسسته، CDF مقادیر احتمال را تا آن چیزی که ما مشخص می کنیم و برای توابع توزیع پیوسته، مساحت زیر تابع چگالی احتمال را تا مقدار مشخص شده می دهد.
جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تحلیل آماری چیست مطالعه نمایید.
2- فرمول تابع توزیع تجمعی
CDF برای یک متغیر تصادفی گسسته تعریف شده و به صورت زیر داده می شود
Fx(x) = P(X ≤ x)
که در آن X احتمالی است که مقداری کمتر یا مساوی x می گیرد و در بازه نیمه بسته [a,b)، جایی که a < b قرار دارد.
بنابراین احتمال درون بازه به صورت نوشته می شود
P(a < X ≤ b) = Fx(b) – Fx(a)
CDF تعریف شده برای یک متغیر تصادفی پیوسته به صورت داده شده است.
در اینجا X بر حسب ادغام تابع چگالی احتمال آن fx بیان می شود.
در صورتی که توزیع متغیر تصادفی X دارای جزء گسسته در مقدار b باشد،
![]()
3- ویژگی های تابع توزیع تجمعی
تابع توزیع تجمعی Fx(x) یک متغیر تصادفی دارای ویژگی های مهم زیر است:
- هر تابع توزیع تجمعی Fx غیر کاهشی و راست پیوسته است
limx→-∞Fx(x) = 0 و limx→+∞Fx(x) = 1
برای همه اعداد حقیقی a و b با متغیر تصادفی پیوسته X، تابع fx برابر با مشتق Fx است، به طوری که
![]()
اگر X یک متغیر تصادفی کاملا گسسته باشد، آنگاه مقادیر x3، x2، x1،… را با احتمال pi = p(xi) می گیرد و CDF X در نقاط xi ناپیوسته خواهد بود:
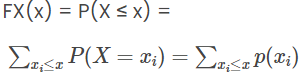
این تابع برای همه مقادیر واقعی تعریف می شود، گاهی اوقات به جای تعریف صریح، به طور ضمنی تعریف می شود. CDF یک مفهوم جدایی ناپذیر از PDF (تابع توزیع احتمال) است.
یک مثال ساده برای CDF در نظر بگیرید که با چرخاندن یک قالب شش وجهی منصفانه ارائه می شود، که در آن X متغیر تصادفی است.
می دانیم که احتمال نتیجه گیری با چرخاندن یک قالب شش وجهی به صورت زیر است:
احتمال به دست آوردن 1 = P(X≤ 1) = 1/6
احتمال به دست آوردن 2 = P(X≤ 2 ) = 2/6
احتمال بدست آوردن 3 = P(X≤ 3 ) = 3/6
احتمال بدست آوردن 4 = P(X≤ 4 ) = 4/6
احتمال بدست آوردن 5 = P(X≤ 5 ) = 5/6
احتمال به دست آوردن 6 = P(X≤ 6 ) = 6 / 6 = 1
از این رو، اشاره می شود که مقدار احتمال همیشه بین 0 و 1 قرار دارد و ماهیت آن غیر کاهشی و راست پیوسته است.
4- توزیع فرکانس تجمعی
مجموعه ای از داده هایی که به صورت جدولی یا گرافیکی نمایش داده می شوند و فراوانی مشاهدات را در یک بازه زمانی مشخص نشان می دهد، توزیع فرکانس است. در مورد بسامد تجمعی، تعداد مشاهداتی که فراتر از هر مشاهده خاصی رخ می دهد محاسبه می شود.
5- کاربردهای تابع توزیع تجمعی
مهمترین کاربرد CDF در تحلیل های آماری استفاده می شود. در تحلیل های آماری از مفهوم CDF به دو صورت استفاده می شود.
- یافتن فراوانی وقوع مقادیر برای پدیده های داده شده با استفاده از تحلیل فراوانی تجمعی.
- برای استخراج برخی از خصوصیات آماری ساده، با استفاده از یک تابع توزیع تجربی، که از یک تخمین مستقیم رسمی از CDFها استفاده می کند.
6- مثال تابع توزیع تجمعی
سوال:
متغیر تصادفی با PDF :
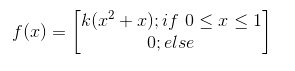
تابع توزیع تجمعی (CDF) را پیدا کنید
راه حل: متغیر تصادفی با تابع توزیع احتمال به ما داده می شود. اکنون CDF را پیدا کنیم.

7- سوالات متداول
منظور از تابع توزیع تجمعی چیست؟
تابع توزیع تجمعی (CDF) متغیر تصادفی X به صورت FX(x) = P(X ≤ x)، برای تمام x ∈ R تعریف می شود. توجه داشته باشید که زیرنویس X نشان می دهد که این CDF متغیر تصادفی X است. همچنین ، توجه داشته باشید که CDF برای تمام x ∈ R تعریف شده است.
CDF چه کاری انجام می دهد؟
تابع توزیع تجمعی (CDF) احتمال تجمعی را برای یک مقدار x معین محاسبه می کند. از CDF برای تعیین احتمال اینکه یک مشاهده تصادفی گرفته شده از جامعه کمتر یا مساوی با یک مقدار خاص باشد، استفاده کنید.
PDF و CDF چیست؟
برای یک تابع پیوسته، تابع چگالی احتمال (PDF) احتمالی است که متغیر مقدار x را داشته باشد. برای توزیع های پیوسته، احتمال در یک نقطه واحد صفر است. به طور کلی، این را می توان در قالب یکپارچگی بین دو نقطه بیان کرد.
تابع توزیع تجمعی (CDF) یک متغیر تصادفی با ارزش واقعی X، که در x ارزیابی میشود، تابع احتمالی است که X مقداری کمتر یا مساوی x میگیرد. برای توصیف توزیع احتمال متغیرهای تصادفی در یک جدول استفاده می شود. و با کمک این داده ها می توانیم به راحتی یک نمودار CDF در یک برگه اکسل ایجاد کنیم.
محدوده مقادیر تابع توزیع تجمعی چقدر است؟
تابع توزیع تجمعی، FX(t) از 0 تا 1 متغیر است.
آیا CDF همیشه در حال افزایش است؟
CDF می تواند افزایش یا به شدت افزایش یابد. هر زمان که در مجموعه مقادیری که متغیر می تواند بگیرد، ناپیوستگی وجود داشته باشد، یک CDF به شدت افزایش نمی یابد: به عنوان مثال، یک توزیع گسسته.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











