آزمون ریشه واحد یا مانایی چیست؟

چکیده مقاله :
ریشه واحد (unit root) که فرآیند ریشه واحد یا فرآیند ثابت تفاوت نیز نامیده می شود، یک روند تصادفی در یک سری زمانی است که گاهی اوقات “random walk with drift” نامیده می شود. اگر یک سری زمانی یک ریشه واحد داشته باشد، یک الگوی سیستماتیک را نشان می دهد که غیرقابل پیش بینی است. دلیل اینکه چرا آن را ریشه واحد می نامند به دلیل ریاضیات پشت این فرآیند است. در یک سطح پایه، یک فرآیند را می توان به عنوان یک سری از تک اسم ها (عبارات با یک جمله منفرد) نوشت. هر مونومی مربوط به یک ریشه است. اگر یکی از این ریشه ها برابر با 1 باشد، این یک ریشه واحد است. در این مطلب به طور کامل به مفهوم آزمون ریشه واحد یا مانایی می پردازیم با ما همراه باشید.
آزمون ریشه واحد چیست؟
آزمون ریشه واحد یک روش آماری است که در اقتصاد سنجی برای تعیین اینکه آیا مجموعه داده سری زمانی ثابت نیست و دارای ریشه واحد است یا خیر، استفاده می شود. ریشه واحد نشان میدهد که یک متغیر تحت تأثیر شوکهای تصادفی قرار میگیرد و تمایل دارد در طول زمان به میانگین خود بازگردد، که نشاندهنده عدم وجود روند یا ثبات بلندمدت است. این آزمون ها در اقتصاد سنجی برای تجزیه و تحلیل داده های اقتصادی استفاده می شوند.
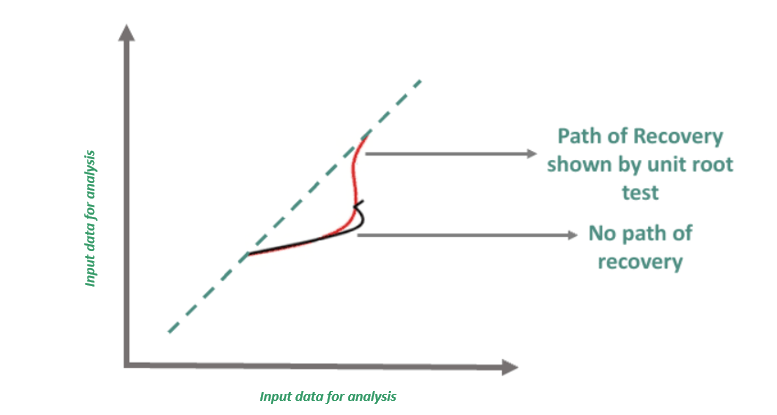
دادههای سری زمانی ثابت برای مدلسازی و پیشبینی دقیق در تحلیلهای آماری بسیار مهم است. از این رو، محققان، اقتصاددانان و تحلیلگران از آزمون ریشه واحد برای تأیید اینکه آیا ویژگی های آماری مانند میانگین و واریانس در طول زمان ثابت مانده اند استفاده می کنند. اگر یک سری غیر ثابت باشد (حاوی ریشه واحد)، می تواند منجر به نتایج رگرسیون گمراه کننده و پیش بینی های غیر قابل اعتماد شود. این به این دلیل اتفاق می افتد که ویژگی های آماری داده های غیر ثابت در طول زمان تغییر می کند.
- انواع داده های در آمار
مفاهیم کلیدی
- آزمون ریشه واحد به یک اندازه گیری اقتصاد سنجی اشاره دارد که به محققین کمک می کند تا ثابت یا غیر ثابت بودن یک سری زمانی را شناسایی کنند.
- برخی از روش های استاندارد عبارتند از: آزمایش دیکی-فولر تقویت شده (ADF)، دیکی-فولر (DF) و فیلیپس-پرون (PP).
- رد فرضیه صفر آزمون ریشه واحد نشان دهنده ایستایی است و داده ها را برای مدل ها و تحلیل های سری زمانی مختلف مناسب می کند.
- چنین آزمونهایی حیاتی هستند، زیرا اعتبار تحلیلهای آماری را تضمین میکنند، دقت پیشبینی را بهبود میبخشند و پایه محکمی برای تحقیقات اقتصادی و سیاستگذاری فراهم میکنند.
تست های ریشه واحد یا مانایی
تست ریشه واحد ابزار ضروری در تحلیل سری های زمانی است. آنها برای تعیین اینکه آیا یک متغیر غیر ساکن است (دارای ریشه واحد) یا ثابت است استفاده می شود. یک متغیر غیر ثابت (همانطور که از نام آن پیداست) متغیری است که میانگین، واریانس یا خودهمبستگی در طول زمان تغییر میکند. متغیر ثابت متغیری است که در آن ویژگی های آماری در طول زمان بدون تغییر باقی می مانند.
تست های ریشه واحد زیادی در اقتصاد سنجی و تجزیه و تحلیل سری های زمانی وجود دارد که در زیر مورد بحث قرار می گیرد:
تست دیکی-فولر تقویت شده (ADF)
در زمینه تست ADF، یک ریشه واحد نشان میدهد که این سری از یک الگوی پیادهروی تصادفی پیروی میکند، که در آن تغییرات از یک دوره به دوره دیگر سازمانیافته و غیرقابل پیشبینی هستند.
تست دیکی فولر (DF)
این نسخه سادهتر تست ADF است که تفاوتهای تاخیر اضافی در معادله رگرسیون را شامل نمیشود.
تست فیلیپس پرون (PP)
مشابه ADF، تست PP یک ریشه واحد را بررسی می کند و خطاهایی مانند همبستگی خودکار و ناهمسانی را در سری داده شده تصحیح می کند. این به ویژه برای تجزیه و تحلیل داده های غیر عادی یا داده هایی که حاوی مقادیر پرت هستند مفید است زیرا بر اساس رگرسیون ناپارامتریک است. رگرسیون ناپارامتریک هیچ فرضی را در مورد توزیع اساسی داده های مورد نظر ایجاد نمی کند.
تست (ERS)
این تست به طور خاص برای رسیدگی به شکست های ساختاری در داده های سری زمانی طراحی شده است که امکان تجزیه و تحلیل قوی تر را در حضور چنین نویزهایی فراهم می کند. شکست های ساختاری به تغییرات در روندها یا الگوهای اساسی یک سری زمانی اشاره دارد.
تست Zivot-Andrews
زمانی استفاده می شود که ممکن است یک شکست ساختاری در داده ها وجود داشته باشد. این یک توسعه آزمایش ADF است که امکان شکست ساختاری در یک نقطه ناشناخته از سری را فراهم می کند. شکست ساختاری یک تغییر ناگهانی و دائمی در سطح یا روند یک سری زمانی است.
فرمول آزمون ریشه واحد
بر اساس مفروضات، فرمول آزمون ریشه واحد به صورت زیر متفاوت است:
مورد 1 – بدون ثابت و ترند:
δYt-1+ut
مورد 2 – با ثابت:
α+δYt-1+ut
مورد 3 – با ثابت و روند:
α+βT+δYt-1+ut
مثال هایی از آزمون ریشه واحد
آزمایش ریشه واحد باعث می شود فرآیند تحلیلی یکپارچه و کارآمد باشد. اجازه دهید کاربرد آن را در سناریوهای خاص درک کنیم.
مثال شماره 1
فرض کنید لورا، مدیر فروش شرکت ABC، از آزمون ریشه واحد برای تجزیه و تحلیل مجموعه داده های سری زمانی برای یکی از فروشگاه های خرده فروشی خود استفاده می کند. در این مورد، او می خواهد داده های فروش ماهانه را تجزیه و تحلیل کند. او آزمایش دیکی-فولر (ADF) را برای داده های فروش اعمال می کند. هدف از این آزمون تعیین این است که آیا دادهها یک ریشه واحد را نشان میدهند که نشاندهنده یک حرکت تصادفی و رفتار غیر ثابت است یا اینکه در طول زمان ثابت است.
فرضیه صفر آزمون ریشه واحد آزمون ADF بیان می کند که ریشه های واحد در نمونه سری زمانی وجود دارد. اگر آمار آزمون محاسبه شده به طور قابل توجهی کمتر از مقادیر بحرانی باشد، می توان فرضیه صفر را رد کرد. این رد نشان میدهد که دادهها ثابت هستند، بدون ریشه واحد، که آن را برای پیشبینی دقیق و درک الگوهای اساسی در دادههای فروش ارزشمند میسازد.
حالا بیایید ببینیم لورا با انجام این کار به چه چیزی دست می یابد. او قبل از اتخاذ تصمیمات مهم اطمینان می دهد که داده های فروش ثابت هستند. این به این دلیل است که داده های ثابت احتمالاً دقیق تر هستند و کیفیت و ارتباط تصمیمات تجاری را بهبود می بخشند.
مثال شماره 2
فرض کنید تغییرات قیمت سهام یک سهم خاص در ده سال گذشته بدون روند ثابت به شرح زیر است:
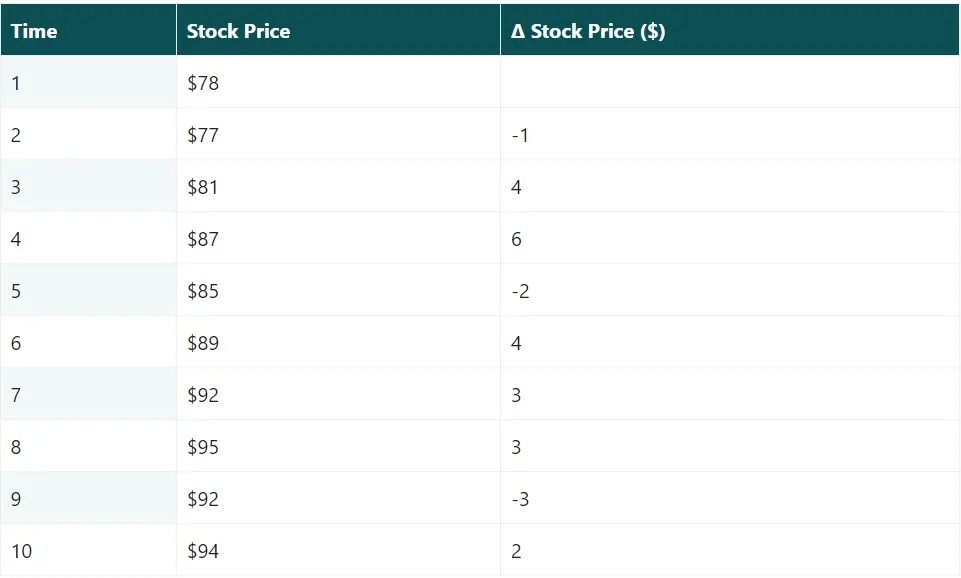
از آنجایی که سری هیچ روند ثابتی ندارد، می توان از فرمول δYt-1+ut برای یافتن سری زمانی استفاده کرد. با استفاده از این آزمون، تحلیلگران الگوهای حرکت قیمت را شناسایی می کنند و تعیین می کنند که آیا این داده ها ثابت هستند یا غیر ثابت. درنتیجه آنها را قادر می سازد تا تصمیم بگیرند و بازار را پیش بینی کنند.
کاربردهای آزمون ریشه واحد
در زیر چند راه برای استفاده از آزمون ریشه واحد ذکر شده است:
- برای پیشبینی متغیرهای اقتصادی با ایجاد ترتیب ادغام استفاده میشود.
- به تحلیل رفتار بلندمدت متغیرهای اقتصادی کمک می کند.
- آزمون ریشه واحد امکان بررسی قیمت سهام، نرخ ارز و سایر متغیرهای مالی را برای ارزیابی روندهای آتی در این زمینه ها فراهم می کند.
- این آزمون ها برای متغیرهای کلان اقتصادی مانند تولید ناخالص داخلی، تورم و نرخ بیکاری برای درک الگوها و روابط بلندمدت آنها اعمال می شود.
- آنها با مدل های قیمت گذاری دارایی برای تعیین ثابت بودن متغیرهای مورد استفاده در این مدل ها استفاده می شوند.
- مطالعات زیست محیطی از این آزمون ها برای تجزیه و تحلیل داده های سری زمانی مربوط به آلودگی، آب و هوا و سایر عوامل محیطی استفاده می کنند.
- نظارت، کنترل و بهبود کیفیت محصولات در ساخت در طول زمان با مطالعه نتایج به دست آمده از آزمایشات ریشه واحد امکان پذیر است.
- یک کاربرد عمده که در سطح کلان اقتصادی کمک می کند، تجزیه و تحلیل الگوهای شیوع بیماری، پیامدهای بیمار یا هزینه های مراقبت های بهداشتی است.
با این حال، مانند سایر تکنیک های آماری، این اندازه گیری نیز مستعد محدودیت های خاصی است. در درجه اول، نتایج آن می تواند به اندازه نمونه حساس باشد و حتی با تغییرات جزئی در متغیرهای ورودی به نتایج متفاوتی منجر شود. همچنین، فرض میکند که فرآیند زیربنایی خطی است، که ممکن است همیشه اینطور نباشد. حتی نمی تواند اطلاعاتی در مورد ترتیب ادغام یا وجود شکست های ساختاری در داده ها ارائه دهد.
علاوه بر این، تفسیر آن بسیار چالش برانگیز است و به دانش قوی اقتصاد سنجی نیاز دارد. علاوه بر این، نتایج ممکن است همیشه قطعی نباشند و نیاز به تجزیه و تحلیل و آزمایش گسترده با روشهای دیگر داشته باشند.
با این حال، آزمایشهای ریشه واحد به طور گسترده در موقعیتهایی که به تحلیل سریهای زمانی نیاز است استفاده میشود. از این رو، استفاده از آن در ارتباط با سایر روشهای آزمایش ممکن است عاقلانه باشد.
اهمیت آزمون های ریشه واحد
آزمونهای ریشه واحد ابزارهای ضروری در تحلیل سریهای زمانی و اقتصادسنجی هستند. آنها نقش مهمی در تعیین اینکه آیا یک مجموعه داده سری زمانی معین ثابت یا غیر ثابت است ایفا می کنند. اهمیت آن را می توان به صورت زیر بیان کرد:
- برای مدلسازی سریهای زمانی حیاتی است: استفاده از مدلهای سری زمانی مانند رگرسیون خودکار برداری (VAR) و میانگین متحرک یکپارچه بازگشتی خودکار (ARIMA) را تسهیل میکند، که نیاز به ثابت بودن دادهها دارد و میانگین و واریانس ثابت را در طول زمان نشان میدهد.
- از رگرسیون کاذب اجتناب میکند: از آنجایی که سریهای زمانی غیر ثابت میتوانند منجر به نتایج رگرسیون کاذب شوند، جایی که سریهای نامرتبط صرفاً به این دلیل که هر دو ترند دارند، مرتبط به نظر میرسند، آزمایش ثابت به شناسایی و رسیدگی به این موضوع کمک میکند.
- دقت پیشبینی را افزایش میدهد: سریهای ثابت الگوهای قابل پیشبینی بیشتری را نشان میدهند و پیشبینی دقیق آنها را آسانتر میکنند. از این رو، آزمون ریشه واحد به تحلیلگران در انتخاب مدل های مناسب برای چنین تحلیلی کمک می کند.
- تسهيل تدوين سياست و تحقيقات اقتصادي: در حوزه اقتصاد، چنين آزمونهايي براي اتخاذ تصميمات سياستي و تحقيقات اقتصادي كه متكي بر تفسير الگوهاي زيربنايي در متغيرهاي اقتصادي شناسايي شده از طريق اين آزمون است، ضروري هستند.
- از تفسیر نادرست جلوگیری می کند: این تست ها یک رویکرد سیستماتیک برای ارزیابی ثابت بودن یک سری زمانی ارائه می دهند و تحلیلگران را از تفسیر نادرست نتایج یا نتیجه گیری نادرست در مورد الگوهای داده نجات می دهد. تحلیلگران بازاریابی، تحلیلگران مالی و محققان نمونه هایی از حرفه ای هستند که از این روش تست به نفع خود استفاده می کنند.
- تجزیه و تحلیل هم انباشتگی: چنین آزمون هایی در تحلیل هم انباشتگی اساسی هستند که به درک روابط تعادلی مختلف بین متغیرهای اقتصادی کمک می کند. تجزیه و تحلیل هم انباشتگی برای شناسایی روابط بلندمدت بین سری های زمانی داده شده مفید است، که به کاهش یا حذف رگرسیون کاذب کمک می کند.
سوالات متداول
1. بهترین تست ریشه واحد کدام است؟
محبوب ترین تست ریشه واحد، تست دیکی-فولر تقویت شده (ADF) است. این به طور گسترده در تجزیه و تحلیل آماری برای شناسایی وجود نقاط پرت در یک سری زمانی معین از داده ها و سنجش عدم ایستایی استفاده می شود. با این حال، سایر ابزارهای رایج مورد استفاده، آزمون های Kwiatkowski-Phillips-Schmidt-Shin (KPSS) و Phillips-Perron (PP) هستند.
2. چرا تست های ریشه واحد را انجام می دهیم؟
هدف اصلی این آزمون اطمینان از پایایی تحلیل و پیشبینی سریهای زمانی با تأیید ثابت بودن آن است. از این رو، این یک معیار به طور گسترده ای در امور مالی و اقتصادی برای مدل سازی دقیق الگوهای داده است.
3. آزمایش ریشه واحد نسل اول چیست؟
آزمایش ریشه واحد نسل اول یک روش اقتصاد سنجی اولیه است که برای تعیین اینکه آیا مجموعه داده سری زمانی یک ریشه واحد را نشان می دهد یا خیر. یکی از برجستهترین آزمایشهای ریشه واحد نسل اول، تست دیکی-فولر تقویتشده (ADF) است. این آزمون آزمون دیکی-فولر را با ترکیب متغیرهای وابسته ای که مقادیر را در معادله رگرسیون عقب می اندازند، گسترش می دهد.
4. تست ریشه واحد را چه کسی اختراع کرد؟
اولین آزمون ریشه واحد در سال 1976 توسط فولر پیشنهاد شد. بعدها، دیکی و فولر با هم آزمون دیکی-فولر (DF) را در سال 1979 و آزمون دیکی-فولر تقویت شده (ADF) را در سال 1981 ارائه کردند.
مدیر2025-11-06T00:58:39+03:30نوامبر 6, 2025|0 Comments
چکیده مقاله: GEO کلاه سیاه معبری است به دنیایی که وسوسه موفقیت سریع را با تکنیک های پرخطر همزمان می کند؛ روش هایی که تحت عناوین Black Hat GEO شناخته می شوند و شامل [...]
مدیر2025-10-29T18:11:45+03:30اکتبر 29, 2025|0 Comments
چکیده مقاله: دنیای دیجیتال هر روز در حال تغییر است و کاربران دیگر مثل گذشته به دنبال کلیک روی ده ها لینک نیستند. آن ها پاسخ را می خواهند، آن هم سریع، دقیق و [...]
مدیر2025-10-28T01:13:42+03:30اکتبر 28, 2025|0 Comments
چکیده مقاله: بهینه سازی موتور مولد (GEO) یکی از رویکردهای نوین در حوزه بهبود عملکرد سیستم های تولید محتوا و مدل های زبانی است که با هدف افزایش کیفیت، دقت و کارایی خروجی های [...]
مدیر2025-10-25T22:04:29+03:30اکتبر 25, 2025|0 Comments
چکیده مقاله: بهترین شامپو تقویت کننده مو انتخابی حیاتی برای افرادی است که به سلامت و زیبایی موهای خود اهمیت می دهند. امروزه با افزایش تنوع محصولات مراقبتی، تشخیص یک شامپوی واقعا مؤثر که [...]
مدیر2025-10-14T23:14:28+03:30اکتبر 14, 2025|0 Comments
چکیده مقاله: تفاوت AEO و SEO موضوعی است که در سال های اخیر توجه بسیاری از متخصصان دیجیتال مارکتینگ را به خود جلب کرده است. با گسترش استفاده از موتورهای جستجو و ابزارهای هوشمند [...]
مدیر2025-10-14T13:30:28+03:30اکتبر 13, 2025|0 Comments
چکیده مقاله: تفاوت GEO و SEO یکی از مهم ترین موضوعات داغ دنیای بازاریابی دیجیتال در عصر هوش مصنوعی است. تا همین چند سال پیش، هدف اصلی سئو این بود که سایت شما در [...]












خیلی کامل و عالی بود ممنون
سلام وقت بخیر
ممنون از دلگرمی خوبتون