آزمون F: تست F با فرمول، محاسبه و مثال دستی و اکسل

چکیده مقاله:
آزمون F یا F test یک اصطلاح کلی برای هر آزمونی است که از توزیع F استفاده می‌کند. در اکثر موارد، وقتی مردم درباره آزمون F صحبت می‌کنند، در واقع منظورشان تست F برای مقایسه دو واریانس است. با این حال، آمار F در انواع مختلفی از آزمون‌ها، از جمله تحلیل رگرسیون، آزمون چاو (Chow test) و آزمون شفل (Scheffé Test) که یک آزمون پس از تحلیل واریانس (ANOVA) است، استفاده می شود. این آزمون‌ها به ما کمک می‌کنند تا روابط بین متغیرها را بررسی کرده و تصمیم گیری های آماری دقیقی انجام دهیم. در نتیجه، درک بهتر آزمون F و کاربردهای آن می‌تواند به تحلیل‌های پیچیده‌تر و استنتاج های دقیق‌تر منجر شود.

آزمون F یک آزمون آماری است که در آزمون فرضیه‌ها برای بررسی این که آیا واریانس های دو جامعه یا دو نمونه برابر هستند یا خیر، استفاده می شود. در یک آزمون F، داده‌ها پیرو توزیع F هستند. این آزمون از آمار F برای مقایسه دو واریانس با تقسیم آن‌ها استفاده می‌کند. تست F می‌تواند یک طرفه یا دو طرفه باشد که بسته به پارامترهای مسئله مشخص می‌شود.

مقدار F که پس از انجام آزمون F به دست می‌آید، برای انجام آزمون ANOVA (تحلیل واریانس) یک طرفه استفاده می‌شود. در این مقاله، بیشتر درباره تست F، آمار F، مقدار بحرانی آن، فرمول و چگونگی انجام آزمون F برای آزمون فرضیه ها خواهیم آموخت.

آزمون F در آمار چیست؟

آزمون F در آمار، آزمونی است که بر روی توزیع F انجام می‌شود. تست F دو طرفه برای بررسی این که آیا واریانس‌های دو نمونه (یا جوامع) داده شده برابر هستند یا خیر، استفاده می‌شود. با این حال، اگر یک تست F بررسی کند که آیا واریانس یک جامعه بزرگ‌تر یا کوچک‌تر از دیگری است، به آزمون فرضیه یک طرفه تبدیل می‌شود.

تست F می‌تواند به عنوان آزمونی تعریف شود که از آمار آزمون F برای بررسی این که آیا واریانس های دو نمونه (یا جوامع) برابر هستند یا خیر، استفاده می کند. برای انجام تست F، جامعه باید پیرو توزیع F باشد و نمونه ها باید رویدادهای مستقل باشند. هنگام انجام آزمون فرضیه، اگر نتایج تست F از نظر آماری معنی‌دار باشند، فرض صفر می تواند رد شود، در غیر این صورت نمی توان آن را رد کرد.

نکات مهم درباره آزمون F

• تست F یک آزمون آماری است که بر روی توزیع F انجام می‌شود تا برابری واریانس های دو جمعیت را بررسی کند.
• فرمول آزمون F برای آمار آزمون به صورت زیر است:
  F = σ²₁ / σ²₂
• مقدار بحرانی F یک مقدار قطع است که برای بررسی این‌که آیا فرض صفر را می‌توان رد کرد یا خیر، استفاده می‌شود.
• ANOVA یک طرفه نمونه‌ای از تست F است که برای بررسی تغییرپذیری میانگین گروه ها و تغییرپذیری مربوط به مشاهدات درون گروه استفاده می‌شود.

این نکات می‌توانند به درک بهتر تست F و کاربردهای آن در تجزیه و تحلیل‌های آماری کمک کنند.

فرمول آزمون F

آزمون F برای بررسی برابری واریانس ها با استفاده از آزمون فرضیه به کار می‌رود. فرمول تست F برای آزمون‌های فرضیه مختلف به شرح زیر است:

Left Tailed Test:

فرض صفر: H₀: σ²₁ = σ²₂

فرض جایگزین: H₁: σ²₁ < σ²₂

معیار تصمیم گیری: اگر آمار F < مقدار بحرانی F، فرض صفر را رد کنید.

Right Tailed test:

فرض صفر: H₀: σ²₁ = σ²₂

فرض جایگزین: H₁: σ²₁ > σ²₂

معیار تصمیم گیری: اگر آمار آزمون F > مقدار بحرانی تست F، فرض صفر را رد کنید.

Two Tailed test:

فرض صفر: H₀: σ²₁ = σ²₂

فرض جایگزین: H₁: σ²₁ ≠ σ²₂

معیار تصمیم‌گیری: اگر آمار تست F> مقدار بحرانی آزمون F، فرض صفر رد می‌شود.

آمار F

آمار آزمون F یا به سادگی آمار F، مقداری است که با مقدار بحرانی مقایسه می‌شود تا بررسی کند آیا فرض صفر باید رد شود یا خیر. فرمول آمار تست F به شرح زیر است:

آمار F برای نمونه‌های بزرگ: F = σ²₁ / σ²₂، که در آن σ²₁ واریانس جامعه اول و σ²₂ واریانس جامعه دوم است.

آمار F برای نمونه‌های کوچک: F = s²₁ / s²₂، که در آن s²₁ واریانس نمونه اول و s²₂ واریانس نمونه دوم است.

معیار انتخاب برای σ²₁ و σ²₂ در آمار F به شرح زیر است:

• برای آزمون با دم راست و آزمون دو دم، واریانس با مقدار بزرگ تر در صورت کسر قرار می گیرد. بنابراین، نمونه مربوط به σ²₁ به عنوان نمونه اول در نظر گرفته می‌شود. واریانس با مقدار کوچک‌تر در مخرج قرار می گیرد و به نمونه دوم تعلق دارد.
• برای آزمون با دم چپ، واریانس کوچک تر به عنوان صورت کسر (نمونه ۱) و واریانس بزرگ‌تر به عنوان مخرج (نمونه ۲) در نظر گرفته می شود.

مقدار بحرانی آزمون F

مقدار بحرانی نقطه‌ای است که آمار آزمون با آن مقایسه می‌شود تا تصمیم بگیرد آیا فرض صفر را رد کند یا خیر. به صورت گرافیکی، مقدار بحرانی توزیع را به دو منطقه پذیرش و رد تقسیم می‌کند. اگر آمار آزمون در منطقه رد قرار گیرد، فرض صفر می‌تواند رد شود وگرنه نمی توان آن را رد کرد. مراحل پیدا کردن مقدار بحرانی آزمون F در سطح آلفای خاص (یا سطح معنی داری) به شرح زیر است:

درجات آزادی نمونه اول را پیدا کنید. این کار با کم کردن ۱ از اندازه نمونه اول انجام می‌شود. بنابراین، x = n₁ – ۱. ۲. درجات آزادی نمونه دوم را با کم کردن ۱ از اندازه نمونه پیدا کنید. بنابراین، y = n₂ – ۱. ۳. اگر آزمون راست‌طرفه باشد، α سطح معنی‌داری است. برای آزمون چپ‌طرفه ۱ – α سطح آلفا است. با این حال، اگر آزمون دو طرفه باشد، سطح معنی داری برابر با α / ۲ است. ۴. جدول F برای پیدا کردن مقدار بحرانی در سطح آلفای مورد نیاز استفاده می‌شود. ۵. تلاقی ستون x و ردیف y در جدول F مقدار بحرانی آزمون F را می‌دهد.

آزمون F در ANOVA

ANOVA یک طرفه نمونه ای از آزمون F است. ANOVA به معنی تحلیل واریانس است. این آزمون برای بررسی تغییرپذیری میانگین گروه‌ها و تغییرپذیری مرتبط با مشاهدات درون آن گروه استفاده می‌شود. آمار تست F برای انجام آزمون ANOVA استفاده می‌شود. فرضیه به شرح زیر است:

H₀: میانگین‌های تمام گروه‌ها برابر هستند.

H₁: میانگین‌های تمام گروه‌ها برابر نیستند.

آمار آزمون: F = واریانس توضیح داده شده / واریانس توضیح داده نشده

قاعده تصمیم‌گیری: اگر F > مقدار بحرانی F، فرض صفر را رد کنید.

برای تعیین مقدار بحرانی آزمون ANOVA، درجات آزادی به صورت زیر محاسبه می‌شوند: df₁ = K – ۱ و df₂ = N – K، که در آن N اندازه کل نمونه و K تعداد گروه‌ها است.

مراحل کلی برای انجام آزمون F

اگر شما قصد دارید تست F را انجام دهید، بهتر است از نرم‌افزارهایی مانند Excel، SPSS، Minitab یا سایر تکنولوژی‌ها استفاده کنید. چرا؟ زیرا محاسبه آزمون F به‌صورت دستی، از جمله محاسبه واریانس‌ها، کار طاقت‌فرسا و زمان‌بر است و احتمالاً در این فرآیند اشتباهاتی نیز به وجود خواهد آمد.

اگر از تکنولوژی برای اجرای آزمون F (برای مثال، تست F برای دو نمونه واریانس‌ها در Excel) استفاده کنید، تنها مراحل ۱ و ۴ (مرتبط با فرض صفر) را باید انجام دهید. تکنولوژی مراحل ۲ و ۳ را برای شما محاسبه خواهد کرد.

مراحل انجام آزمون F:

1. بیان فرض صفر و فرض جایگزین:

• فرض صفر (H₀): واریانس‌ها برابر هستند.
• فرض جایگزین (H₁): واریانس‌ها برابر نیستند.

2. محاسبه مقدار F:
   • مقدار F با استفاده از فرمول زیر محاسبه می‌شود:
     F = (SSE₁ – SSE₂) / m) / (SSE₂ / (n – k)
     که در آن:
     SSE = مجموع مربعات باقی‌مانده
     m = تعداد محدودیت‌ها
     k = تعداد متغیرهای مستقل
3. یافتن آمار F (مقدار بحرانی برای این آزمون):
   • فرمول آمار F به صورت زیر است:
     آمار F = واریانس میانگین گروه‌ها / میانگین واریانس‌های درون گروه
   • شما می‌توانید آمار F را در جدول F پیدا کنید.
4. حمایت یا رد فرض صفر:
   • پس از محاسبه مقدار F و مقایسه آن با مقدار بحرانی، شما می‌توانید تصمیم بگیرید که آیا فرض صفر را رد کنید یا آن را تایید کنید. اگر مقدار محاسبه شده F بزرگ‌تر از مقدار بحرانی باشد، فرض صفر رد می‌شود.

با استفاده از این مراحل و تکنولوژی‌های مناسب، می‌توانید آزمون F را به‌راحتی و با دقت بیشتری انجام دهید.

• آنالیز میانگین-واریانس

تفاوت آزمون F و آزمون T

آزمون F و آزمون T انواع مختلفی از آزمون‌های آماری هستند که بسته به توزیع داده های جمعیت برای آزمون فرضیه استفاده می شوند. در ادامه، تفاوت های اصلی بین آزمون F و آزمون T بررسی می‌شود.

• آزمون T در آمار

تست F یک آمار آزمون است که برای بررسی برابری واریانس‌های دو جمعیت استفاده می‌شود. در حالی که آزمون T زمانی استفاده می‌شود که اندازه نمونه کوچک باشد (n < 30) و انحراف معیار جمعیت ناشناخته باشد.

• انواع داده ها در آمار با ذکر مثال

داده‌ها در تست F تابع توزیع F هستند، در حالی که داده‌ها در آزمون T تابع توزیع t استیودنت هستند.

آمار آزمون F به صورت زیر است:
F = σ²₁ / σ²₂

آمار آزمون T برای یک نمونه به صورت زیر است:

t = (¯x – μ) / (s / √n)، که در آن ¯x میانگین نمونه، μ میانگین جمعیت، s انحراف معیار نمونه و n اندازه نمونه است.

در نهایت، آزمون F برای بررسی واریانس‌ها استفاده می‌شود، در حالی که آزمون T برای آزمون میانگین ها به کار می‌رود.

این تفاوت‌ها به شما کمک می‌کنند تا درک بهتری از شرایط استفاده از هر یک از این آزمون‌ها داشته باشید و انتخاب مناسبی برای تحلیل‌های آماری خود انجام دهید.

• تحلیل آماری

آزمون F برای مقایسه دو واریانس

آزمون آماری F از آمار F برای مقایسه دو واریانس، s₁ و s₂، با تقسیم آن‌ها استفاده می‌کند. نتیجه همیشه یک عدد مثبت خواهد بود (زیرا واریانس‌ها همیشه مثبت هستند). معادله برای مقایسه دو واریانس با آزمون F به صورت زیر است:
F = s²₁ / s²₂

اگر واریانس‌ها برابر باشند، نسبت واریانس‌ها برابر با ۱ خواهد بود. به عنوان مثال، اگر دو مجموعه داده با نمونه ۱ (واریانس ۱۰) و نمونه ۲ (واریانس ۱۰) داشته باشید، نسبت به صورت زیر خواهد بود:
۱۰/۱۰ = ۱

همیشه در اجرای آزمون F فرض می‌شود که واریانس‌های جمعیت برابر هستند. به عبارت دیگر، شما همیشه فرض می‌کنید که واریانس‌ها برابر با ۱ هستند. بنابراین، فرض صفر شما همیشه این خواهد بود که واریانس‌ها برابرند.

فرضیات

چندین فرض برای این آزمون وجود دارد. جمعیت شما باید تقریباً به طور نرمال توزیع شود (یعنی شکل منحنی زنگی را داشته باشد) تا بتوانید از این آزمون استفاده کنید. همچنین، نمونه‌ها باید رویدادهای مستقل باشند. علاوه بر این، نکات مهم زیر را باید در نظر داشته باشید:

• واریانس بزرگ‌تر همیشه باید در صورت کسر (عدد بالایی) قرار گیرد تا آزمون به یک آزمون یک طرفه (راست) تبدیل شود. آزمون های یک طرفه محاسبه راحت تری دارند.
• برای آزمون های دوطرفه، مقدار آلفا را قبل از یافتن مقدار بحرانی صحیح، بر ۲ تقسیم کنید.
• اگر انحراف معیار ها به شما داده شده باشند، باید آن‌ها را مربع کنید تا واریانس‌ ها به دست آید.
• اگر درجات آزادی شما در جدول F ذکر نشده باشد، از بزرگ ترين مقدار بحرانی استفاده کنید. این کار به جلوگیری از احتمال خطاهای نوع I کمک می‌کند.

این فرضیات و نکات می توانند به شما در درک بهتر آزمون F و شرایط استفاده از آن کمک کنند.

• تفاوت انحراف استاندارد و واریانس

مراحل انجام تست F برای مقایسه دو واریانس به صورت دستی

آزمون F می‌تواند محاسبات وقت گیری داشته باشد، به‌ویژه اگر بخواهید واریانس‌ها را محاسبه کنید. بنابراین، بهتر است از نرم‌افزارهایی مانند Excel استفاده کنید. در ادامه مراحل عمومی برای انجام تست F به صورت دستی آورده شده است.

مرحله ۱:

اگر انحراف معیارها به شما داده شده‌اند، به مرحله ۲ بروید. اگر واریانس‌ها برای مقایسه به شما داده شده‌اند، به مرحله ۳ بروید.

مرحله ۲:

هر دو انحراف معیار را مربع کنید تا واریانس ها به دست آید. به عنوان مثال، اگر σ₁ = 9.6 و σ₂ = 10.9 باشد، آنگاه واریانس‌ها (s₁ و s₂) به صورت زیر خواهند بود:
s₁ = 9.6² = 92.16 و s₂ = 10.9² = 118.81.

مرحله ۳:

بزرگ‌ترین واریانس را بگیرید و آن را بر کوچک‌ترین واریانس تقسیم کنید تا مقدار F به دست آید. به عنوان مثال، اگر دو واریانس شما s₁ = 2.5 و s₂ = 9.4 باشد، محاسبه به صورت زیر خواهد بود:

9.4 / 2.5 = 3.76

چرا؟ قرار دادن بزرگ ترین واریانس در صورت کسر، آزمون F را به یک آزمون یک طرفه (راست) تبدیل می‌کند که محاسبه آن بسیار آسان‌تر از آزمون یک طرفه (چپ) است.

مرحله ۴:

درجات آزادی خود را پیدا کنید. درجات آزادی برابر است با اندازه نمونه منهای ۱. از آنجایی که دو نمونه دارید (واریانس ۱ و واریانس ۲)، دو درجه آزادی خواهید داشت: یکی برای صورت کسر و دیگری برای مخرج.

مرحله ۵:

مقدار F که در مرحله ۳ محاسبه کرده‌اید را در جدول F جستجو کنید. توجه داشته باشید که چندین جدول وجود دارد، بنابراین باید جدول مناسب را برای سطح آلفای خود پیدا کنید.

مرحله ۶:

مقدار محاسبه شده (مرحله ۳) را با مقدار F در جدول (مرحله ۵) مقایسه کنید. اگر مقدار جدول F از مقدار محاسبه‌شده کوچکتر باشد، می‌توانید فرض صفر را رد کنید.

با دنبال کردن این مراحل، می‌توانید تست F را به‌طور دستی انجام دهید و به نتایج دقیقی برسید.

آزمون F دو طرفه

تفاوت بین اجرای آزمون F یک‌طرفه و دوطرفه این است که سطح آلفا برای آزمون‌های دوطرفه باید نصف شود. به عنوان مثال، به جای استفاده از α = 0.05، از α = 0.025 استفاده می‌کنید؛ و به جای استفاده از α = 0.01، از α = 0.005 استفاده می‌کنید.

در تست F دوطرفه، شما فقط می‌خواهید بدانید که آیا واریانس‌ها با یکدیگر برابر نیستند. به صورت نمادین:
Hₐ = σ²₁ ≠ σ²₂

مثال: انجام آزمون F دوطرفه بر روی نمونه‌های زیر:

نمونه ۱: واریانس = ۱۰۹.۶۳، اندازه نمونه = ۴۱
نمونه ۲: واریانس = ۶۵.۹۹، اندازه نمونه = ۲۱

مرحله ۱: نوشتن فرضیات

• H₀: هیچ تفاوتی در واریانس‌ها وجود ندارد.
• Hₐ: تفاوتی در واریانس‌ها وجود دارد.

مرحله ۲: محاسبه مقدار بحرانی F

بزرگ‌ترین واریانس را به عنوان صورت کسر و کوچک‌ترین واریانس را به عنوان مخرج در نظر بگیرید:
آمار F = واریانس ۱ / واریانس ۲ = ۱۰۹.۶۳ / ۶۵.۹۹ = ۱.۶۶

مرحله ۳: محاسبه درجات آزادی

درجات آزادی در جدول برابر است با اندازه نمونه منهای ۱، بنابراین:

• نمونه ۱ دارای ۴۰ درجه آزادی (صورت کسر) است.
• نمونه ۲ دارای ۲۰ درجه آزادی (مخرج) است.

مرحله ۴: انتخاب سطح آلفا

در سوال هیچ سطح آلفایی ذکر نشده است، بنابراین از ۰.۰۵ (که در آمار استاندارد است) استفاده کنید. این مقدار باید برای آزمون دوطرفه نصف شود، بنابراین از ۰.۰۲۵ استفاده کنید.

مرحله ۵: یافتن مقدار بحرانی F با استفاده از جدول F

چندین جدول وجود دارد، بنابراین مطمئن شوید که در جدول مربوط به α = ۰.۰۲۵ نگاه می‌کنید. مقدار بحرانی F برای (۴۰، ۲۰) در سطح α = ۰.۰۲۵ برابر با ۲.۲۸۷ است.

مرحله ۶: مقایسه مقدار محاسبه شده با مقدار جدول

حالا مقدار محاسبه شده F (مرحله ۲) را با مقدار F در جدول (مرحله ۵) مقایسه می‌کنیم. اگر مقدار محاسبه شده بالاتر از مقدار جدول باشد، می‌توانیم فرض صفر را رد کنیم:

• مقدار محاسبه‌شده F: برایر ۱.۶۶
• مقدار F از جدول: ۲.۲۸۷

بنابراین:
۱.۶۶ < ۲.۲۸۷

با توجه به این مقایسه، نمی توانیم فرض صفر را رد کنیم.

آزمون F برای مقایسه دو واریانس در اکسل

مراحل تست F دو نمونه‌ای برای واریانس‌ها در اکسل ۲۰۱۳:

مرحله ۱: بر روی زبانه “Data” کلیک کنید و سپس بر روی “Data Analysis” کلیک کنید.

مرحله ۲: بر روی “F test two sample for variances” کلیک کنید و سپس “OK” را فشار دهید.

مرحله ۳: بر روی کادر Variable 1 Range کلیک کرده و سپس محل اولین مجموعه داده‌های خود را وارد کنید. به عنوان مثال، اگر داده‌های خود را در سلول‌های A1 تا A10 وارد کرده‌اید، “A1” را در این کادر تایپ کنید.

مرحله ۴: بر روی کادر Variable 2 کلیک کرده و سپس محل مجموعه دوم داده‌های خود را وارد کنید. به عنوان مثال، اگر داده‌های خود را در سلول‌های B1 تا B10 وارد کرده‌اید، “B1” را در این کادر تایپ کنید.

مرحله ۵: اگر داده‌های شما دارای عنوان ستون هستند، کادر Labels را انتخاب کنید.

مرحله ۶: یک سطح آلفا انتخاب کنید. در اکثر موارد، سطح آلفا ۰.۰۵ معمولاً مناسب است.

مرحله ۷: محلی برای خروجی خود انتخاب کنید. به عنوان مثال، بر روی دکمه رادیویی “New Worksheet” کلیک کنید.

مرحله ۸: بر روی “OK” کلیک کنید.

مرحله ۹: نتایج را بخوانید. اگر مقدار F محاسبه شده شما بیشتر از مقدار بحرانی F باشد، فرض صفر را رد کنید زیرا دو جمعیت شما دارای واریانس‌های نابرابر هستند.

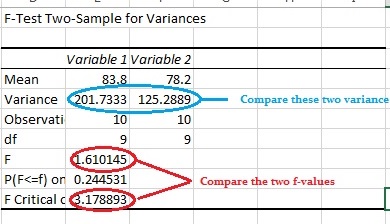
نکته مهم

هشدار: اکسل یک “quirk” کوچک دارد. مطمئن شوید که واریانس ۱ بیشتر از واریانس ۲ باشد. اگر اینطور نیست، داده های ورودی خود را جابه‌جا کنید (یعنی ورودی ۱ را “B” و ورودی ۲ را “A” کنید). در غیر این صورت، اکسل مقدار F نادرستی محاسبه خواهد کرد. این به این دلیل است که واریانس نسبت واریانس ۱ به واریانس ۲ است و اکسل نمی‌تواند تعیین کند که کدام مجموعه داده، مجموعه ۱ و کدام مجموعه، مجموعه ۲ است مگر اینکه شما به‌طور صریح به آن بگویید.