همبستگی چیست؟ تعریف، نحوه محاسبه و مثال

چکیده مقاله:
همبستگی یک معیار آماری است که نشان می دهد تا چه اندازه دو یا چند متغیر نسبت به یکدیگر نوسان دارند. همبستگی مثبت نشان می دهد که آن متغیرها به طور موازی افزایش یا کاهش می یابند؛ در حالی که همبستگی منفی نشان می دهد که با افزایش یکی از متغیرها، دیگری کاهش می یابد. در این مطلب به بررسی کامل مفهوم همبستگی پرداخته و انواع آن را به همراه نحوه محاسبه با ذکر مثال توضیح می دهیم.
همبستگی چیست؟
همبستگی یک معیار آماری است که میزان ارتباط خطی دو متغیر (به این معنا که آنها با نرخ ثابتی تغییر می کنند) را نشان می دهد. این معیار ابزاری رایج برای توصیف روابط ساده بین متغیرها بدون اشاره به رابطه علت و معلولی است.
به عبارت دیگر همبستگی به رابطه آماری بین دو موجودیت یا نحوه حرکت دو متغیر در رابطه با یکدیگر اشاره دارد. برای درک نحوه عملکرد correlation، درک عبارات زیر مفید است:
- همبستگی مثبت: correlation مثبت (1) خواهد بود. این بدان معنی است که دو متغیر با هم در یک جهت بالا یا پایین حرکت کرده اند.
- همبستگی منفی: یک correlation منفی (-1) است. این بدان معنی است که دو متغیر در جهت مخالف حرکت می کنند.
- همبستگی صفر: correlation صفر (0) به این معنی است که بین دو متغیر رابطه وجود ندارد. به عبارت دیگر، زمانی که یک متغیر به یک سمت حرکت می کند، متغیر دیگر در جهت غیرمرتبط حرکت می کند.
مفاهیم کلیدی:
- correlation رابطه بین دو متغیر است و می توان آن را برای اطلاع رسانی تصمیمات مالی و بازاریابی اندازه گیری کرد.
- وقتی دو متغیر در یک جهت حرکت می کنند، correlation می تواند مثبت باشد، زمانی که دو متغیر در جهت مخالف حرکت می کنند منفی یا زمانی که هیچ رابطه ای بین دو متغیر وجود ندارد، صفر باشد.
- انواع همبستگی ها شامل همبستگی پیرسون برای روابط خطی، همبستگی اسپیرمن است که یک رابطه یکنواخت بین متغیرها را تعیین می کند و همبستگی کندال که قدرت وابستگی بین دو مجموعه داده را اندازه گیری می کند.
ضریب همبستگی چیست؟
ضریب همبستگی یک معیار آماری است که نشان می دهد تا چه اندازه تغییرات در مقدار یک متغیر می تواند تغییر در مقدار متغیر دیگر را پیش بینی کند. وقتی نوسانات یک متغیر به طور معتبری نوسانات مشابهی را در متغیر دیگر پیش بینی می کند، اغلب این گرایش وجود دارد که تصور شود تغییر در یکی باعث تغییر در دیگری می شود. اما correlation به معنای رابطه علت و معلولی نیست. ممکن است، برای مثال، یک عامل ناشناخته وجود داشته باشد که هر دو متغیر را به طور مشابه تحت تاثیر قرار دهد. تمایز بین همبستگی و علیت می تواند در درک الگوهای داده های مصرف کننده ارزشمند باشد و بینش های مفیدی ارائه دهد. مثال معروف در این زمینه، رابطه بین فروش آبجو و پوشک است که اغلب در حوزه بازاریابی برای نشان دادن این موضوع به کار می رود.
مثالی برای همبستگی:
تعدادی از مطالعات، همبستگی مثبتی را بین میزان تماشای تلویزیون توسط کودکان و احتمال اینکه آنها به زورگویی تمایل پیدا کنند، گزارش می دهند. رسانه ها اغلب این گونه مطالعات را به عنوان دلیلی برای این که تماشای زیاد تلویزیون باعث می شود کودکان زورگو شوند، معرفی می کنند. اما این مطالعات تنها وجود یک correlation را گزارش می دهند، نه رابطه علت و معلولی. به احتمال زیاد، عامل دیگری مانند نبود نظارت والدین، می تواند عامل اصلی باشد.
همبستگی چگونه اندازه گیری می شود؟
ضریب همبستگی نمونه، که با r نمایش داده می شود، میزان قدرت رابطه را کمّی می کند. همبستگی ها همچنین از نظر اهمیت آماری مورد آزمون قرار می گیرند.
چگونه ضریب همبستگی را محاسبه کنیم؟
می توانید از فرمول زیر برای محاسبه correlation استفاده کنید:
ضریب همبستگی = Σ(x(i) – x̄)(y(i) – ȳ) / √(Σ(x(i) – x̄)² * Σ(y(i) – ȳ)²)
1. تعیین مجموعه دادهها
در ابتدا، متغیرهای مورد نظر را مشخص کنید و دادههای آنها را جمعآوری نمایید. برای راحتی، میتوانید این متغیرها را در دو ستون جداگانه مرتب کنید: یکی برای x و دیگری برای y. به عنوان مثال:
x: (1, 2, 3, 4)
y: (2, 3, 4, 5)
2. محاسبه میانگین متغیرهای x و y
میانگین (یا میانگین حسابی) به شما مقدار مرکزی برای هر مجموعه داده میدهد. برای به دست آوردن میانگین، تمام مقادیر هر متغیر را با هم جمع کرده و سپس بر تعداد مقادیر تقسیم کنید.
- محاسبه میانگین x:
x̄ = (1 + 2 + 3 + 4) / 4 = 2.5 - محاسبه میانگین Y:
ȳ = (2 + 3 + 4 + 5) / 4 = 3.5
3. کم کردن میانگین از مقادیر هر متغیر
در این مرحله، میانگین هر متغیر را از مقادیر آن متغیر کم کنید. این کار به شما نشان میدهد که هر مقدار چقدر از میانگین فاصله دارد.
محاسبه انحرافات برای x:
a(1) = 1 – 2.5 = -1.5
a(2) = 2 – 2.5 = -0.5
a(3) = 3 – 2.5 = 0.5
a(4) = 4 – 2.5 = 1.5
محاسبه انحرافات برای y:
b(1) = 2 – 3.5 = -1.5
b(2) = 3 – 3.5 = -0.5
b(3) = 4 – 3.5 = 0.5
b(4) = 5 – 3.5 = 1.5
4. محاسبه جمع ضرب انحرافات
در این مرحله، هر انحراف از x را با انحراف متناظر در y ضرب کرده و سپس مجموع آنها را به دست آورید. این مجموع در نهایت به عنوان صورت کسر در محاسبه ضریب همبستگی استفاده میشود.
Σ(a(i) * b(i)) = (-1.5 * -1.5) + (-0.5 * -0.5) + (0.5 * 0.5) + (1.5 * 1.5)
= 2.25 + 0.25 + 0.25 + 2.25 = 5
5. محاسبه جمع مربع انحرافات
جمع مربع انحرافات را برای هر متغیر محاسبه کنید. این مقادیر در محاسبه مخرج کسر استفاده میشوند.
Σ(a(i)²) = (-1.5)² + (-0.5)² + (0.5)² + (1.5)²
= 2.25 + 0.25 + 0.25 + 2.25 = 5
Σ(b(i)²) = (-1.5)² + (-0.5)² + (0.5)² + (1.5)²
= 2.25 + 0.25 + 0.25 + 2.25 = 5
6. محاسبه ضریب همبستگی
با استفاده از مقادیر به دست آمده در مراحل قبل، ضریب همبستگی را محاسبه کنید.
r = Σ(a(i) * b(i)) / √(Σ(a(i)²) * Σ(b(i)²)
= 5 / √(5 * 5)
= 5 / 5
= 1
محدودیت های تحلیل همبستگی چیست؟
همبستگی نمی تواند وجود یا تاثیر متغیرهای دیگر را که خارج از دو متغیر مورد بررسی هستند، تحلیل کند. مهم تر از آن، همبستگی به ما چیزی درباره علت و معلول نمی گوید. correlation همچنین نمی تواند روابط غیرخطی را به طور دقیق توصیف کند.
همبستگی ها حرکت داده ها را با هم توصیف می کنند
همبستگی ها برای توصیف روابط ساده بین داده ها مفید هستند. برای مثال، تصور کنید که در حال بررسی مجموعه داده ای از اردوگاه های کوهستانی در یک پارک هستید. می خواهید بدانید که آیا رابطه ای بین ارتفاع اردوگاه (میزان ارتفاع آن از سطح کوه) و دمای متوسط در تابستان وجود دارد یا نه.
برای هر اردوگاه، دو معیار دارید: ارتفاع و دما. وقتی این دو متغیر را در نمونه خود مقایسه می کنید، می توانید یک رابطه خطی پیدا کنید: با افزایش ارتفاع، دما کاهش می یابد. آنها به طور منفی با هم همبسته هستند.
اعداد همبستگی چه معنایی دارند؟
ما همبستگی ها را با یک معیار بدون واحد به نام ضریب correlation بیان می کنیم که در محدوده -1 تا +1 قرار دارد و با r نشان داده می شود. اهمیت آماری با مقدار p-value مشخص می شود. بنابراین، همبستگی ها معمولاً با دو عدد کلیدی نشان داده می شوند: r = و p = .
هر چه r به صفر نزدیک تر باشد، رابطه خطی ضعیف تر است. مقادیر مثبت r نشان دهنده correlation مثبت هستند، به این معنا که مقادیر هر دو متغیر تمایل به افزایش با هم دارند. مقادیر منفی r نشان دهنده همبستگی منفی هستند، به این معنا که با افزایش مقادیر یکی، مقادیر متغیر دیگر کاهش می یابد. مقدار p-value شواهدی ارائه می دهد که نشان می دهد ضریب همبستگی در جامعه احتمالاً متفاوت از صفر است، بر اساس آنچه از نمونه مشاهده می کنیم. “معیار بدون واحد” به این معناست که همبستگی ها در مقیاس خودشان وجود دارند: در مثال ما، عدد r در مقیاس ارتفاع یا دما نیست. این موضوع با سایر آمارهای خلاصه متفاوت است. برای مثال، میانگین اندازه گیری های ارتفاع بر روی همان مقیاس متغیر خود قرار دارد.
p-value چیست؟
p-value معیاری از احتمال است که برای آزمون فرضیه ها به کار می رود.
وقتی همبستگی معناداری به دست می آوریم، می توانیم قدرت آن را نیز بررسی کنیم. یک correlation مثبت کامل دارای مقدار 1 و یک همبستگی منفی کامل دارای مقدار -1 است. اما در دنیای واقعی، انتظار نداریم که correlation کامل را مشاهده کنیم، مگر این که یک متغیر در واقع معیار جانشینی برای متغیر دیگر باشد. در واقع، مشاهده یک عدد همبستگی کامل می تواند نشان دهنده خطا در داده ها باشد! برای مثال، اگر به اشتباه فاصله از سطح دریا را به جای دما برای هر اردوگاه ثبت کرده باشید، این مقدار به طور کامل با ارتفاع همبسته خواهد بود.
تجسم همبستگی ها با نمودارهای پراکندگی
برگردیم به مثال قبلی: با افزایش ارتفاع اردوگاه، دما کاهش می یابد. می توانیم این را مستقیماً با یک نمودار پراکندگی مشاهده کنیم. تصور کنید که داده های مربوط به اردوگاه ها را رسم کرده ایم:
هر نقطه در نمودار نشان دهنده یک اردوگاه است که می توان آن را بر اساس ارتفاع و دمای بالای تابستانی در محور x و y قرار داد. ضریب همبستگی (r) نیز نمودار پراکندگی ما را نشان می دهد. این ضریب به ما می گوید که نقاط ترسیم شده در نمودار تا چه اندازه به یک رابطه خطی نزدیک هستند. روابط قوی تر، یا مقادیر r بزرگ تر، نشان دهنده روابطی هستند که نقاط به خطی که بر داده ها برازش داده ایم، نزدیک تر هستند.
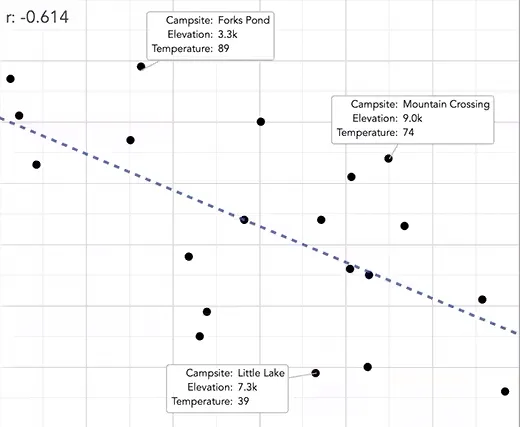
روابط پیچیده تر چطور؟
نمودارهای پراکندگی برای تعیین اینکه آیا الگوی غیرعادی در داده های ما وجود دارد که می تواند مانع از ایجاد همبستگی دقیق شود، مانند الگوهای غیرخطی یا نقاط دورافتاده افراطی، نیز مفید هستند.
همبستگی ها نمی توانند به طور دقیق روابط غیرخطی را تحلیل کنند. در یک رابطه غیرخطی، متغیرها تا یک نقطه خاص در یک جهت همبسته هستند و سپس رابطه تغییر می کند.
برای مثال، تصور کنید که ارتفاع اردوگاه ها و میانگین امتیازاتی که کمپینگ کنندگان به هر اردوگاه داده اند را بررسی می کنیم. ممکن است در ابتدا، ارتفاع و رتبه بندی اردوگاه ها با هم correlation مثبت داشته باشند، زیرا اردوگاه های مرتفع تر دید بهتری از پارک دارند. اما از یک نقطه به بعد، ارتفاع های بالاتر ممکن است به طور منفی با رتبه بندی اردوگاه همبسته باشند، زیرا کمپینگ کنندگان در شب احساس سرما می کنند!
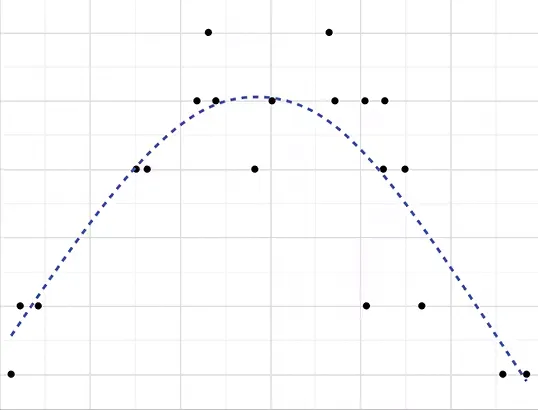
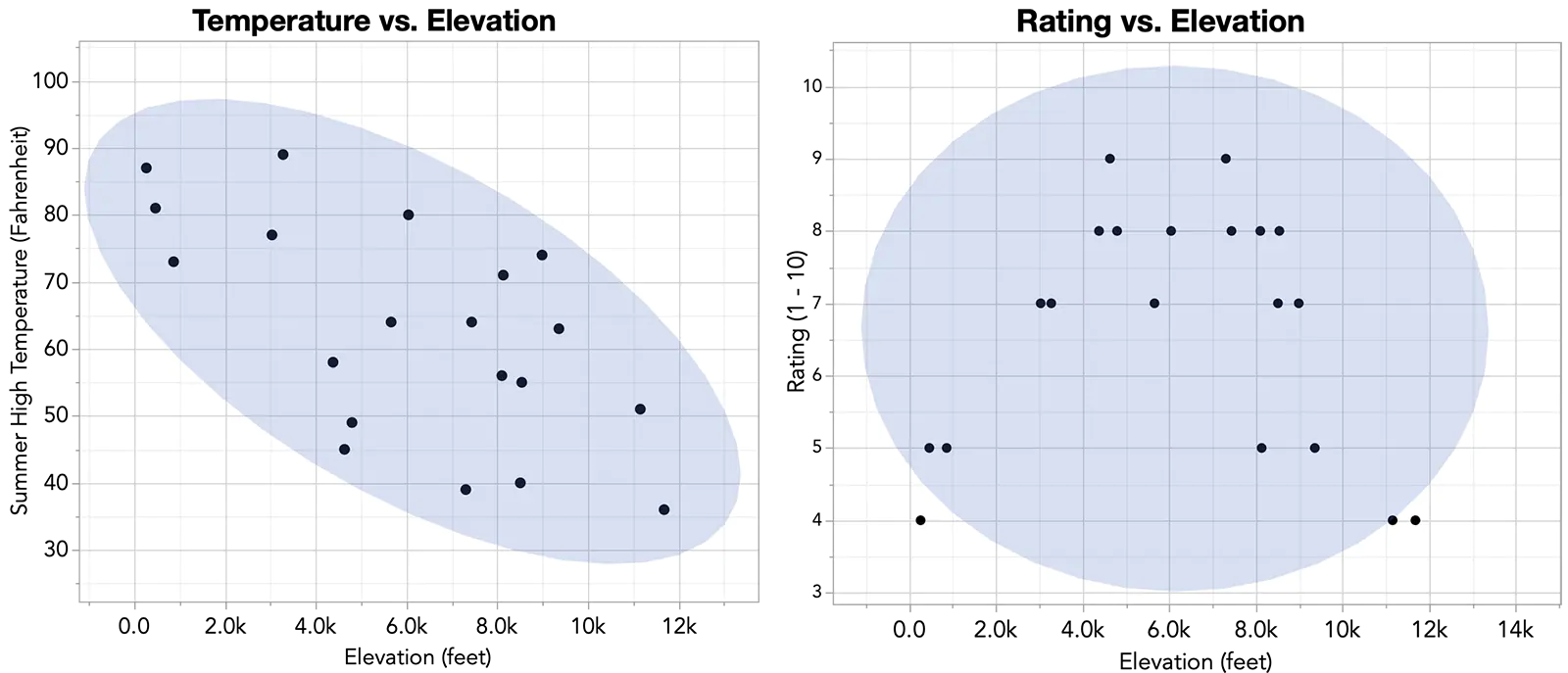
می توانیم با افزودن بیضی های چگالی سایه دار به نمودار پراکندگی، بینش بیشتری به دست آوریم. بیضی چگالی، متراکم ترین ناحیه نقاط در نمودار پراکندگی را نشان می دهد، که به نوبه خود به ما کمک می کند قدرت و جهت همبستگی را ببینیم.
بیضی های چگالی می توانند اندازه های مختلفی داشته باشند. یکی از گزینه های رایج برای بررسی همبستگی، بیضی چگالی 95 درصد است که تقریباً متراکم ترین 95 درصد از مشاهدات را در بر می گیرد. اگر دو متغیر به طور مشترک حرکت کنند، مانند ارتفاع و دمای اردوگاه های ما، انتظار داریم که این بیضی چگالی شکل خط را منعکس کند. و در یک رابطه غیرخطی، بیضی چگالی به شکل گرد در می آید: correlation نمی تواند توصیف معناداری از این رابطه ارائه دهد.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











