فیلتر هودریک پرسکات (HP) چیست؟ راهنمای کامل

چکیده مقاله: فیلتر هودریک پرسکات (Hodrick-Prescott Filter) یک ابزار آماری و اقتصادی است که برای جداسازی روند بلندمدت از نوسانات کوتاه مدت در داده های سری زمانی به کار می رود. این فیلتر، به ویژه در تحلیل های اقتصاد کلان، برای شناسایی چرخه های تجاری و ارزیابی تغییرات ساختاری در داده هایی مانند تولید ناخالص داخلی (GDP)، مصرف و سرمایه گذاری بسیار رایج است. ایده اصلی این روش بر این اساس استوار است که یک سری زمانی را می توان به دو بخش تقسیم کرد: یک روند نرم و هموار که نشان دهنده مسیر بلندمدت داده هاست و یک جزء نوسانی که بازتاب دهنده انحرافات موقتی است. استفاده از این فیلتر به تحلیلگران کمک می کند تا سیگنال های اصلی داده ها را بدون تأثیرپذیری از نویز یا تغییرات تصادفی کوتاه مدت شناسایی کنند و از این طریق تصمیم گیری های اقتصادی و پیش بینی های دقیق تری انجام دهند.

فیلتر هودریک پرسکات (HP) چیست؟

فیلتر هودریک-پرسکات (HP) یک تکنیک هموارسازی داده ها است. این فیلتر معمولاً در تحلیل ها به کار می رود تا نوسانات کوتاه مدت مرتبط با چرخه اقتصادی را حذف کند. حذف این نوسانات کوتاه مدت، روندهای بلندمدت را آشکار می کند. این امر می تواند در پیش بینی اقتصادی یا دیگر پیش بینی های مرتبط با چرخه اقتصادی مفید باشد.

• تحلیل آماری

فیلتر هودریک پرسکات (HP Filter) یک تکنیک آماری است که در تحلیل سری های زمانی برای جداسازی روند بلندمدت (trend) از نوسانات کوتاه مدت (cycle) مورد استفاده قرار می گیرد. این فیلتر نخستین بار توسط دو اقتصاددان، رابرت هودریک و ادوارد پرسکات، برای مطالعه چرخه های اقتصادی معرفی شد و از آن زمان در بسیاری از شاخه های اقتصاد و مالی به کار گرفته شده است. هدف اصلی این فیلتر آن است که مؤلفه هایی از یک سری زمانی که به تغییرات کوتاه مدت مربوط هستند، از روند اصلی که به تغییرات بلندمدت مرتبط است، تفکیک کند. این روش به ویژه در مطالعات کلان اقتصادی، مانند تحلیل تولید ناخالص داخلی (GDP)، اشتغال و تورم، بسیار پرکاربرد است.

فیلتر HP با استفاده از یک مسئله بهینه سازی عمل می کند که در آن هدف، یافتن یک روند هموار است که در عین نزدیکی به داده های واقعی، نوسانات بیش از حد نداشته باشد. این مسئله با کمک یک پارامتر تنظیم (λ) حل می شود که میزان حساسیت فیلتر به نوسانات کوتاه مدت را تعیین می کند. انتخاب مقدار مناسب این پارامتر نقش کلیدی در کارایی فیلتر دارد؛ مقادیر مختلف آن برای داده های با فرکانس های متفاوت (مانند داده های روزانه، ماهانه یا سالانه) توصیه می شود. به دلیل سادگی و انعطاف پذیری، فیلتر HP به یکی از ابزارهای استاندارد در تحلیل های تجربی اقتصادی تبدیل شده است، هرچند که با نقدهایی نیز درباره حساسیت به انتخاب پارامتر و ایجاد نوسانات مصنوعی همراه است.

• تحلیل آماری

نکات کلیدی

• فیلتر هودریک پرسکات یک تکنیک هموارسازی داده ها است که عمدتاً در اقتصاد کلان استفاده می شود.
• این فیلتر معمولاً برای حذف نوسانات کوتاه مدت مرتبط با چرخه اقتصادی در تحلیل ها به کار می رود.
• در عمل، از این فیلتر برای هموارسازی و حذف روندهای کوتاه مدت در شاخص «کمک های درخواستی» هیئت کنفرانس استفاده می شود تا بتوان آن را با داده های «شغل های خالی» اداره آمار کار ایالات متحده (JOLTS) که وضعیت فرصت های شغلی را اندازه گیری می کند، مقایسه کرد.

مفهوم فیلتر هودریک-پرسکات (HP)

فیلتر هودریک-پرسکات ابزاری است که معمولاً در اقتصاد کلان استفاده می شود. این فیلتر به نام اقتصاددانان رابرت هودریک و ادوارد پرسکات نامگذاری شده است که در دهه ۱۹۹۰ این فیلتر را در اقتصاد رواج دادند. هودریک یک اقتصاددان متخصص در حوزه مالی بین الملل بود و پرسکات جایزه نوبل اقتصادی را برای تحقیقاتش در اقتصاد کلان، همراه با یک اقتصاددان دیگر، دریافت کرد.

این فیلتر روند بلندمدت یک سری زمانی را با کاهش اهمیت نوسانات قیمتی کوتاه مدت تعیین می کند. در عمل، این فیلتر برای هموارسازی و حذف روندهای کوتاه مدت شاخص «کمک های درخواستی» (HWI) استفاده می شود تا بتوان آن را با شاخص JOLTS، که یک سری داده اقتصادی دقیق تر درباره فرصت های شغلی در ایالات متحده است، مقایسه کرد.

مفروضات و ملاحظات ویژه در فیلتر هودریک پرسکات

فیلتر هودریک پرسکات یکی از ابزارهای پرکاربرد در تحلیل های اقتصاد کلان است. این فیلتر زمانی که نویز به طور معمولی توزیع شده باشد و تحلیل بر روی داده های تاریخی انجام شود، معمولاً نتایج مطلوبی ارائه می دهد.

با این حال، بر اساس مقاله ای که توسط جیمز همیلتون، اقتصاددان و استاد دانشگاه، منتشر شده و در وب سایت دفتر ملی تحقیقات اقتصادی ایالات متحده (NBER) موجود است، دلایلی وجود دارد که چرا نباید از این فیلتر استفاده شود. همیلتون معتقد است که این فیلتر نتایجی تولید می کند که هیچ پایه و اساسی در فرآیند تولید داده ها ندارند. او همچنین بیان می کند که مقادیر فیلتر شده در انتهای نمونه کاملاً متفاوت از مقادیر وسط نمونه هستند.

فیلتر هودریک پرسکات یک ابزار ریاضی برای تجزیه چرخه ای در تحلیل سری های زمانی

فیلتر هودریک پرسکات (HP) یک تکنیک ریاضی است که برای تجزیه چرخه ای در تحلیل سری های زمانی به کار می رود. این مفهوم در بین اقتصاددانان و در بخش سری های زمانی در یادگیری ماشین محبوب است. هدف از استفاده از این ابزار، حذف نوسانات چرخه ای از یک متغیر زمانی و نمایش رفتار بلندمدت زیربنایی (روند) می باشد.

به عبارت دیگر، این ابزار یک سری زمانی را به دو بخش کوتاه مدت (چرخه ای) و بلندمدت (روند) تقسیم می کند. این ایده کلی را می توان با معادله زیر توضیح داد:

𝑦𝑡=𝜏𝑡+𝑐𝑡

که در آن:

• 𝑦𝑡: ارزش درک شده
• 𝜏𝑡: جزء روند
• 𝑐𝑡: جزء چرخه ای

این توضیح می دهد که مقدار یک متغیر سری زمانی در یک نقطه از زمان (𝑦𝑡 که در آن 𝑡 = 1،2، 3، . . . . n) شامل دو جزء است: یکی از روند (𝜏𝑡) و دیگری به عنوان حرکت چرخه ای (𝑐𝑡). ).

فرضیات کلیدی پیش از پرداختن به روش:

1. هیچ شوک دائمی (با حافظه بلند مدت) یا شکاف در سریال رخ نمی دهد. از آنجایی که این ممکن است برای همیشه سریال را به سطوح جدیدی منتقل کند و بنابراین روند تاریخی دیگر اهمیتی نخواهد داشت.
2. نویز (باقیمانده) در داده ها باید به طور معمول توزیع شود.

فرمول و محاسبه

این مفهوم را می توان با معادله زیر توضیح داد:

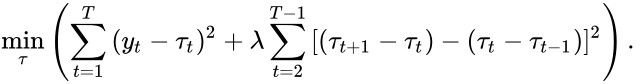
در نگاه اول این معادله ممکن است پیچیده به نظر برسد، اما در اصل، بسیار منطقی و شهودی است. این معادله اساساً یک تابع ضرر را با هدف یافتن مقداری برای مؤلفه روند (𝜏) نشان می دهد که واریانس کلی (مولفه چرخه ای) سری زمانی (𝑦𝑡) را به حداقل می رساند و در نتیجه یک خط روند صاف (𝜏) با حداقل نوسانات ایجاد می کند. (𝑐).

• واریانس چیست؟

به طور همزمان، این معادله همچنین هرگونه حرکت ناگهانی را در روند کلی سری زمانی در طول دوره ها بررسی می کند. این با تفاوت دوم مقدار روند و تنظیم چنین تغییراتی با استفاده از یک فراپارامتر (𝜆) به دست می آید.

بخش اول (تناسب مناسب):

با به حداقل رساندن واریانس کلی روند از سری زمانی زیربنایی، خوبی برازش متغیر روند (𝜏) با داده های سری زمانی کلی (𝑦𝑡) را اندازه گیری می کند. به حداقل رساندن این با توجه به 𝜏 مقدار روند (𝜏) را به دست می دهد که در آن واریانس سری زمانی زیربنایی (𝑦𝑡) حداقل است. این تضمین می کند که روند به طور ایده آل سری زیربنایی خود را توجیه می کند.

• تفاوت انحراف استاندارد و واریانس

بخش دوم (همواری روند):

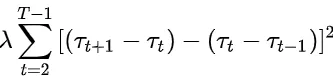
این عبارت با جریمه کردن هرگونه تغییر ناگهانی در شیب متغیر روند، صاف بودن سری روند را تضمین می کند. این عبارت دومین تفاوت متغیر روند (𝜏) را برای بررسی تغییرات بزرگ دوره به دوره در شیب می گیرد. بنابراین، به حداقل رساندن تابع کلی با هدف به دست آوردن یک مقدار 𝜏 است که به طور همزمان تناسب خوبی برای سری های زمانی فراهم می کند و در عین حال هرگونه تغییر ناگهانی در شیب را نیز بررسی می کند، که شهود اساسی در پشت این معادله است.

• کوواریانس چیست؟

بخش سوم پارامتر هموارسازی (λ):

پارامتر λ یک متغیر خارجی تعریف شده در معادله است که بر اساس رفتار خاص سری تنظیم می شود. این پارامتر تعیین می کند تا چه حد اثر تغییرات ناگهانی در رفتار سری زمانی در روند حذف شده در نظر گرفته شود.

• λ کوچک: جریمه کمتری بر تغییرات شیب اعمال می کند، بنابراین روند نزدیک به داده ها باقی می ماند ولی ممکن است نوسانات بیشتری داشته باشد (کمتر هموار باشد).
• λ بزرگ: جریمه بیشتری بر تغییرات شیب اعمال می کند، بنابراین روند هموارتر می شود ولی ممکن است با داده ها فاصله بیشتری داشته باشد.

• آنالیز میانگین-واریانس

چرا نباید از فیلتر هودریک پرسکات استفاده کرد؟

هرچند فیلتر هودریک پرسکات (HP) یکی از ابزارهای رایج در تحلیل سری های زمانی است، اما به دلایل متعددی از جمله محدودیت ها و نقاط ضعف آن، برخی محققان و اقتصاددانان توصیه می کنند که از این فیلتر استفاده نشود یا در استفاده از آن احتیاط شود. در ادامه به برخی از دلایل اصلی این انتقادات اشاره می شود:

1. حساسیت به انتخاب پارامتر تنظیم (λ)
   نتایج حاصل از فیلتر HP به شدت به مقدار پارامتر λ بستگی دارد. این پارامتر، که نقش کلیدی در تفکیک روند و نوسانات کوتاه مدت دارد، باید بر اساس فرکانس داده ها (مانند سالانه، ماهانه یا فصلی) تنظیم شود. با این حال، انتخاب مقدار مناسب $\lambda$ همیشه واضح نیست و می تواند منجر به نتایج متناقض یا گمراه کننده شود. علاوه بر این، هیچ معیار قطعی برای تعیین بهترین مقدار λ وجود ندارد.
2. ایجاد نوسانات مصنوعی
   یکی از مشکلات اساسی فیلتر HP این است که می تواند نوساناتی مصنوعی در داده ها ایجاد کند. این مسئله به ویژه در مرزهای سری زمانی (نقاط ابتدایی و انتهایی داده ها) برجسته تر است، جایی که فیلتر به دلیل کمبود داده های آینده برای پیش بینی دقیق، روند نادرستی را ارائه می دهد. این پدیده که به عنوان اثر مرزی (Edge Effect) شناخته می شود، می تواند منجر به نتایج تحلیلی نادرست شود.
3. نادیده گرفتن ساختار اقتصادی و تئوریک داده ها
   فیلتر HP یک روش مکانیکی است و در فرآیند جداسازی روند و چرخه، هیچ توجهی به ساختار اقتصادی یا تئوریک داده ها ندارد. این مسئله به ویژه در مطالعات کلان اقتصادی مشکل ساز است، چرا که بسیاری از نوسانات کوتاه مدت ممکن است به دلیل شوک های ساختاری یا تغییرات اقتصادی اساسی باشند که نمی توان آنها را صرفاً نویز در نظر گرفت.
4. انتقادات از لحاظ آماری
   مطالعات نشان داده اند که فیلتر HP به طور سیستماتیک تخمین های نادرستی از مؤلفه های چرخه ای ارائه می دهد و در برخی موارد، الگوهای واقعی را تحریف می کند. علاوه بر این، این روش می تواند به همبستگی های نادرست میان سری های زمانی مختلف منجر شود، که در تحلیل روابط میان متغیرها مشکل ساز است.
5. جایگزین های بهتر موجود است
   روش های جایگزین، مانند مدل های ساختاری بیزین (Bayesian Structural Models)، روش های طیفی (Spectral Methods) و تکنیک های مبتنی بر موجک (Wavelet Techniques)، اغلب عملکرد بهتری در جداسازی روند و چرخه ارائه می دهند. این روش ها می توانند مشکلات مربوط به اثر مرزی و حساسیت به پارامتر را کاهش دهند و تحلیل دقیق تری را فراهم کنند.

• انواع داده ها در آمار با ذکر مثال

جمع بندی:

• فیلتر HP سری زمانی را به دو مؤلفه روند و چرخه ای تقسیم می کند.
• بخش تناسب مناسب اطمینان حاصل می کند که روند به داده های واقعی نزدیک باشد.
• بخش همواری روند اطمینان حاصل می کند که روند هموار باقی بماند و تغییرات بزرگ در شیب آن رخ ندهد.
• پارامتر $\lambda$ تعادل بین تطابق نزدیک با داده ها و همواری روند را کنترل می کند.