سیستم غیر خطی شکار و شکارچی Predator–Prey
چکیده مقاله:
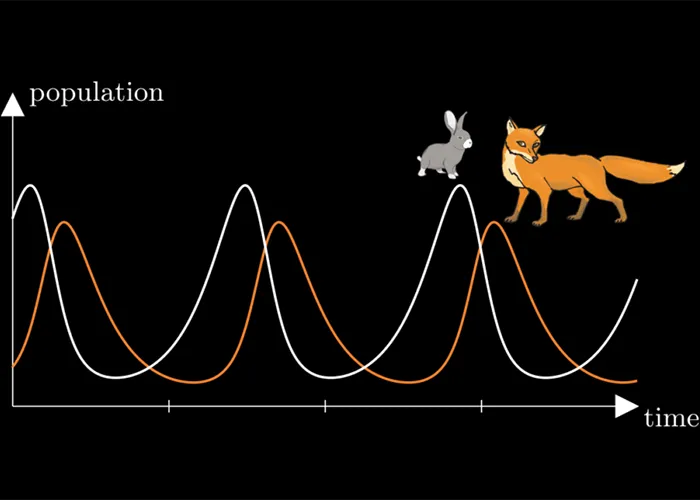
سیستم غیر خطی شکار و شکارچی Predator–Prey یکی از مدل های پایه در زیست شناسی ریاضی و اکولوژی است که رفتار پویا بین دو جمعیت را توصیف می کند؛ یکی به عنوان شکار و دیگری به عنوان شکارچی. این مدل ها بر اساس معادلات دیفرانسیل غیرخطی بنا شده اند و نشان می دهند که چگونه تغییر در جمعیت یک گونه می تواند به تغییرات متقابل در گونه دیگر منجر شود. اهمیت این سیستم در آن است که می تواند چرخه های طبیعی نوسانی جمعیت ها را توضیح دهد، جایی که افزایش جمعیت شکار موجب افزایش شکارچی می شود و سپس با کاهش شکار، جمعیت شکارچی نیز رو به افول می رود.
از دیدگاه ریاضی، مدل های شکار و شکارچی نقطه تلاقی میان نظریه سیستم های پویا و علوم زیستی به شمار می روند. این مدل ها نه تنها به درک بهتر پایداری و ناپایداری اکوسیستم ها کمک می کنند، بلکه به عنوان ابزار تحلیلی در حوزه های مختلف مانند مدیریت منابع طبیعی، زیست شناسی حفاظتی و حتی اقتصاد مورد استفاده قرار می گیرند. بررسی چنین سیستم هایی نشان می دهد که تعاملات ساده در سطح فردی می توانند به رفتارهای پیچیده و غیرقابل پیش بینی در سطح کلان منجر شوند، و همین ویژگی، آنها را به یکی از مهم ترین موضوعات تحقیق در علوم بین رشته ای تبدیل کرده است.
سیستم غیر خطی شکار و شکارچی Predator–Prey یکی از بنیادی ترین مدل های ریاضی در زیست شناسی و علوم کاربردی است که نشان می دهد چگونه تعامل بین دو گونه می تواند چرخه های پیچیده جمعیتی ایجاد کند. این مدل با وجود سادگی ظاهری، توانسته است رفتار های واقعی در طبیعت، اقتصاد، پزشکی و حتی مهندسی را به شکلی دقیق توصیف کند. آنچه این سیستم را جذاب می سازد، پیش بینی نوسان های پایدار بین شکار و شکارچی است؛ پدیده ای که بار ها در اکوسیستم های طبیعی مشاهده شده است. در این مطلب، به معرفی کامل این مدل، تحلیل نقاط تعادل، بررسی نمودار ها و کاربرد های گسترده آن خواهیم پرداخت تا دید عمیق تری از این الگوی مهم در اختیار شما قرار گیرد.
سیستم غیر خطی شکار و شکارچی Predator–Prey
سیستم غیر خطی شکار و شکارچی Predator–Prey چیست؟
تعریف ساده سیستم غیر خطی شکار و شکارچی Predator–Prey
یکی از مهم ترین مدل های ریاضی در تحلیل پویایی جمعیت، مدل شکار و شکارچی است که به عنوان یکی از کلاسیک ترین نمونه های سیستم غیر خطی شکار و شکارچی Predator–Prey شناخته می شود. این مدل نخستین بار توسط دو دانشمند به نام های لوتکا و ولترا ارائه شد و امروزه در رشته های مختلفی مثل زیست شناسی، اقتصاد، پزشکی و حتی مهندسی کاربرد دارد. اساس این مدل بر این است که دو گونه در طبیعت وجود دارند، یکی شکار است و دیگری شکارچی. شکارچی برای بقا به شکار وابسته است و در مقابل، شکار در نبود شکارچی می تواند آزادانه رشد کند.
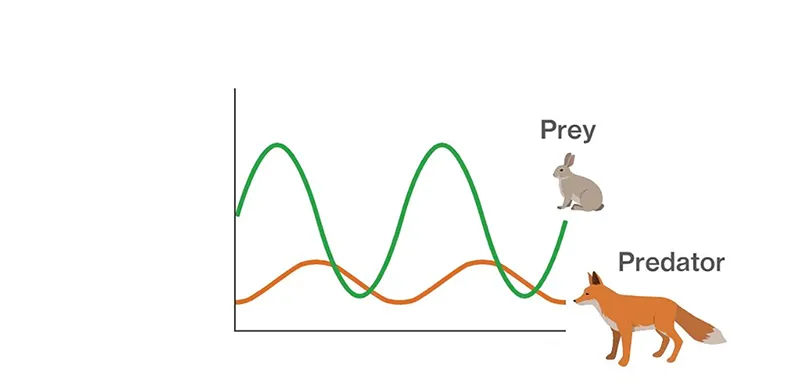
فرض کنید دو گونه در طبیعت داریم، یکی شکار (مثلا خرگوش) و دیگری شکارچی (مثلا گرگ). جمعیت شکار را x(t) و جمعیت شکارچی را y(t) در نظر می گیریم. اگر هیچ شکارچی وجود نداشته باشد، جمعیت شکار با نرخ طبیعی خود رشد می کند. این رشد را می توان با معادله دیفرانسیل dx/dt = ax نمایش داد که در آن a یک ثابت مثبت است. در این حالت جمعیت شکار به صورت نمایی افزایش می یابد.
از طرف دیگر، اگر هیچ شکار وجود نداشته باشد، جمعیت شکارچی ها با نرخ طبیعی خود کاهش پیدا می کند. این موضوع با معادله dy/dt = -by مدل می شود که b یک ثابت مثبت است. در این حالت جمعیت شکارچی ها به مرور زمان کاهش یافته و اگر شرایط تغییری نکند، منقرض خواهند شد.
وقتی این دو جمعیت با هم تعامل می کنند، شکارچی ها افزایش پیدا می کنند زیرا منبع غذایی دارند و شکارها کاهش می یابند زیرا خورده می شوند. نرخ این تغییرات متناسب با حاصلضرب x و y یا همان تعداد برخوردهای شکار و شکارچی در طبیعت است. در نتیجه مدل نهایی به صورت زیر نوشته می شود:
dx/dt = ax – pxy
dy/dt = qxy – by
که در آن a، b، p و q ثابت های مثبت هستند. این همان چیزی است که تحت عنوان سیستم غیر خطی شکار و شکارچی Predator–Prey شناخته می شود.
مفروضات پایه مدل
فرض کنیم دو گونه داریم:
- جمعیت شکار را x(t) می نامیم.
- جمعیت شکارچی را y(t) می نامیم.
در غیاب شکارچی، جمعیت شکار با نرخ طبیعی خود رشد می کند:
dx/dt = ax
که در آن a یک ثابت مثبت است. حل این معادله به صورت x(t) = x0e^(at) خواهد بود. این یعنی شکار در نبود شکارچی به صورت نمایی افزایش می یابد.
در طرف مقابل، اگر هیچ شکاری وجود نداشته باشد، جمعیت شکارچی ها کاهش پیدا می کند:
dy/dt = -by
که b یک ثابت مثبت است. در این حالت شکارچی ها به مرور زمان از بین خواهند رفت.
زمانی که این دو جمعیت با هم تعامل کنند، شکارچی ها با تغذیه از شکار افزایش پیدا می کنند و شکارها به دلیل خورده شدن کاهش می یابند. این نرخ تغییرات متناسب با حاصلضرب x و y است. در نتیجه:
dx/dt = ax – pxy
dy/dt = qxy – by
این سیستم که به معادلات لوتکا-ولترای معروف است، یکی از مشهورترین نمونه های سیستم غیر خطی در علوم کاربردی است.
نقاط تعادل و تحلیل ریاضی
این مدل دو نقطه تعادل دارد: (0,0) و (b/q , a/p). برای تحلیل رفتار سیستم در اطراف این نقاط از استفاده می شود:
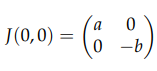
ماتریس ژاکوبین
- نقطه تعادل اول (0,0):
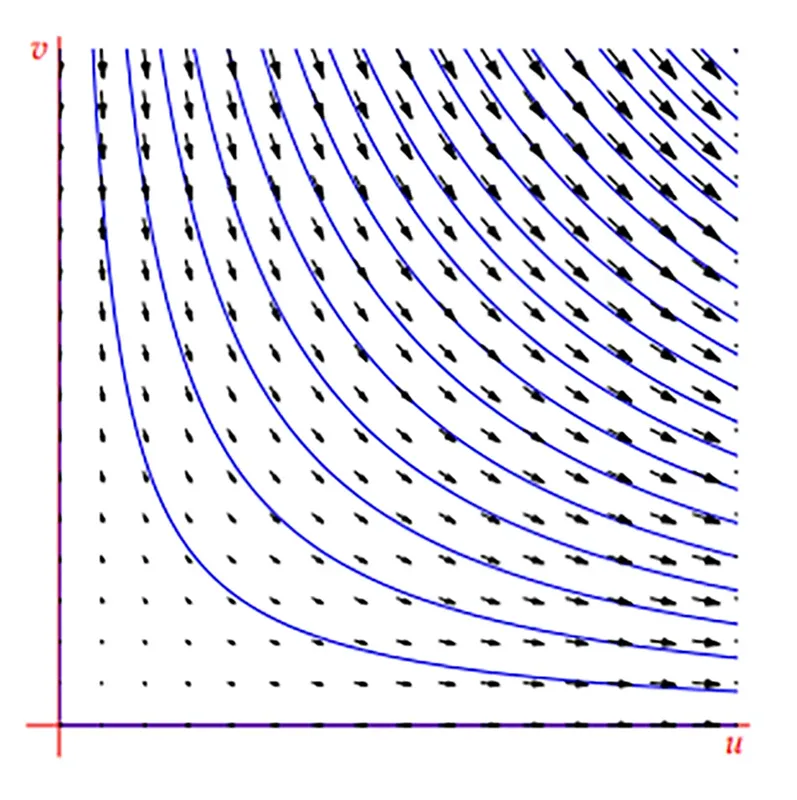
فاز پرتره در اطراف نقطه تعادل (0,0) در مدل سیستم غیر خطی شکار و شکارچی Predator–Prey که نشان دهنده وجود نقطه زین است.
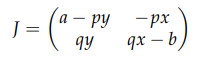
ماتریس ژاکوبین در حالت نشان دهنده انقراض هر دو جمعیت: سیستم غیر خطی شکار و شکارچی
این نشان می دهد که نقطه (0,0) یک زین (saddle point) است. از نظر زیستی این حالت نشان دهنده انقراض هر دو جمعیت است.
- نقطه تعادل دوم (b/q , a/p)
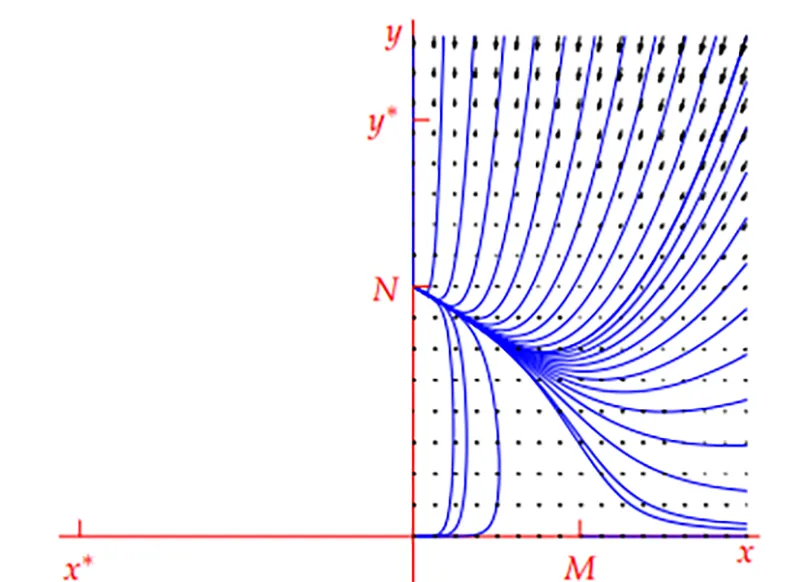
مدارهای بسته نوسانی اطراف نقطه (b/q , a/p) که بیانگر وجود مرکز پایدار است.
در این نقطه مقادیر ویژه به صورت purely imaginary به دست می آیند. این یعنی یک مرکز پایدار (stable center) وجود دارد. بنابراین اگر جمعیت ها مثبت باشند، نوسان های دوره ای حول این نقطه شکل می گیرند.
چرخه های جمعیتی
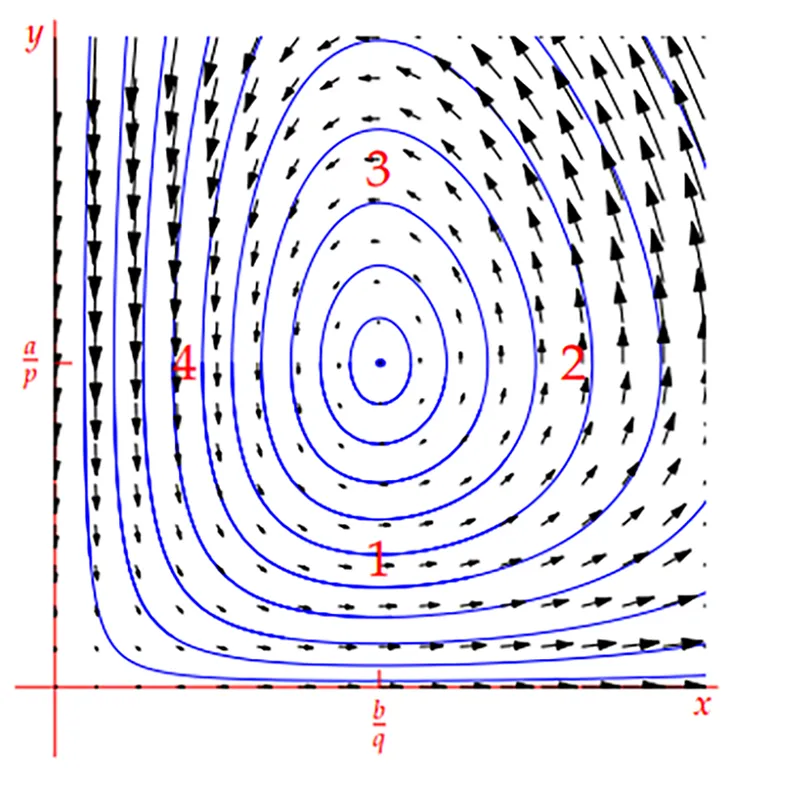
چهار وضعیت جمعیتی در مدل شکار و شکارچی: 1- رشد شکار، 2- افزایش شکارچی، 3- کاهش شکار، 4- کاهش شکارچی
مدل سیستم غیر خطی شکار و شکارچی Predator–Prey نشان می دهد که جمعیت ها رفتار چرخه ای دارند:
زمانی که شکارچی ها کم باشند، جمعیت شکار رشد می کند. افزایش شکار باعث می شود غذای بیشتری برای شکارچی وجود داشته باشد و جمعیت شکارچی بالا برود. وقتی شکارچی زیاد شد، شکار کاهش می یابد. کمبود شکار دوباره جمعیت شکارچی را پایین می آورد و چرخه از نو آغاز می شود.
حل ضمنی معادلات
با روش های ریاضی می توان رابطه ای بین جمعیت شکار و شکارچی به صورت ضمنی نوشت:
a ln y + b ln x = qx + py + C
که C یک ثابت است. این رابطه نشان می دهد مسیر های جمعیتی روی منحنی های بسته قرار می گیرند که بیانگر چرخه های پایدار هستند.
مدل های پیچیده تر: رقابت
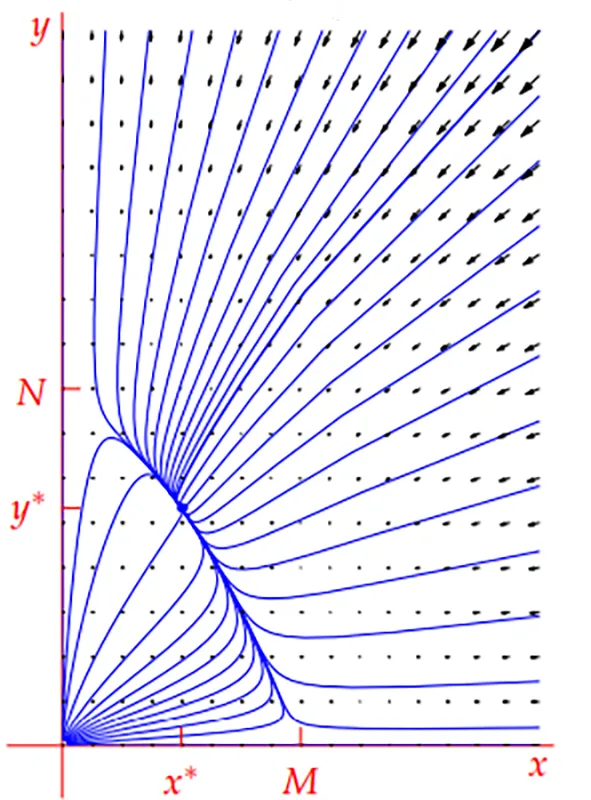
رقابت دو گونه که در آن یک گونه رقیب را حذف کرده و گونه دیگر باقی می ماند.
در بسیاری از شرایط طبیعی، گونه ها صرفا در رابطه شکارچی–شکار قرار ندارند بلکه برای منابع مشترک رقابت می کنند. این حالت با افزودن معادلات لجستیک مدل سازی می شود:
dx/dt = kx(M – x) – pxy
dy/dt = ly(N – y) – qxy
این مدل نشان می دهد که بسته به شرایط محیط، یا یکی از گونه ها منقرض می شود، یا هر دو گونه به تعادل مشترک می رسند.
تحلیل رقابت و پایداری
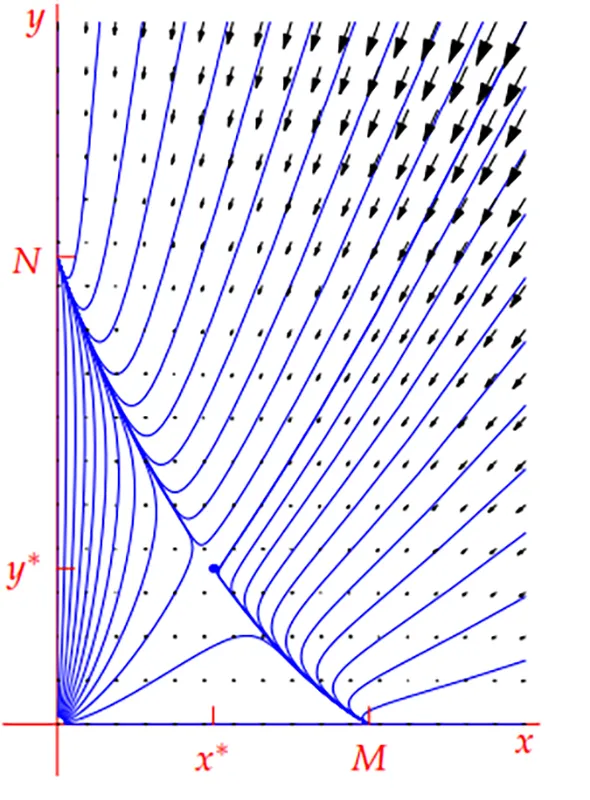
رقابت دو گونه در شرایطی که امکان همزیستی یا حذف بستگی به مقادیر پارامترها و شرایط اولیه دارد.
اگر نقطه تعادل داخلی (x*, y*) در ربع اول باشد، هر دو گونه مثبت و پایدار هستند. اگر در ربع های دیگر باشد، این نقطه زیستی معنا ندارد.
وقتی kl > pq باشد، اثر محدودیت درونی قوی تر از اثر رقابت است و گونه ها می توانند همزیستی داشته باشند. اما اگر kl < pq باشد، رقابت غلبه می کند و یک گونه حذف می شود.
مدل همکاری
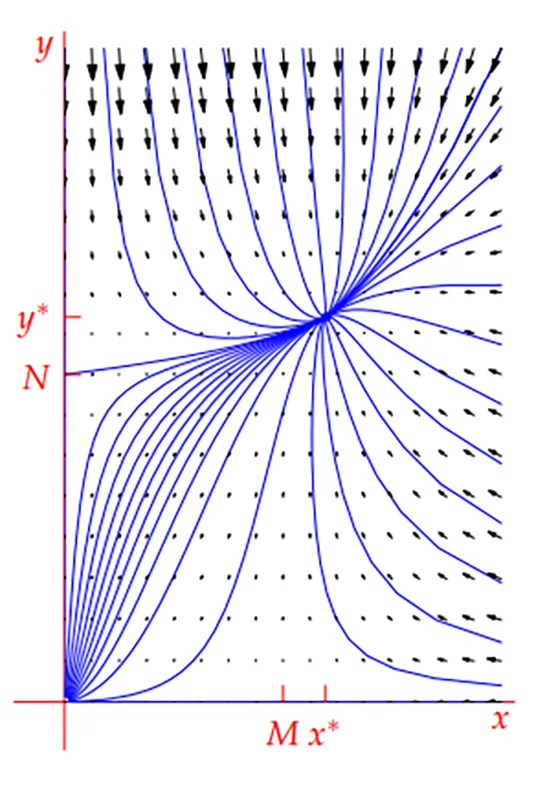
همکاری میان دو گونه که می تواند به جمعیت پایدار بالاتر یا انفجار جمعیتی منجر شود.
حالت دیگری نیز وجود دارد: اگر p و q منفی باشند، گونه ها به جای رقابت، همکاری می کنند. در این شرایط هر دو گونه از حضور یکدیگر سود می برند و جمعیت ها می توانند به سطح بالاتری برسند.
کاربرد های گسترده سیستم غیر خطی شکار و شکارچی
مدل سیستم غیر خطی شکار و شکارچی Predator–Prey نه تنها در زیست شناسی بلکه در علوم دیگر نیز کاربرد دارد:
- در اقتصاد، برای تحلیل رقابت میان شرکت ها و بازارها.
- در پزشکی، برای مدل سازی تعامل میان ویروس ها و سلول های ایمنی یا بررسی رشد تومورها.
- در مهندسی، برای طراحی سیستم های پایدار و تحلیل شبکه ها.
جمع بندی
مدل لوتکا-ولترای نشان می دهد حتی معادلات ساده می توانند چرخه های پیچیده ایجاد کنند. این مدل پایه ای برای بسیاری از تحقیقات علمی است و درک عمیق تری از تعاملات پویا در اختیار ما قرار می دهد. به همین دلیل، سیستم غیر خطی شکار و شکارچی Predator–Prey همچنان یکی از مهم ترین و پرکاربرد ترین ابزار های تحلیل در علوم مختلف است.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











