آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test)

چکیده مقاله:
آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) یکی از روش های آماری غیرپارامتری پرکاربرد است که برای مقایسه دو گروه وابسته یا بررسی تغییرات یک متغیر در دو وضعیت متفاوت استفاده می شود. این آزمون زمانی مورد توجه قرار می گیرد که داده ها از توزیع نرمال پیروی نکنند و استفاده از آزمون های پارامتری مانند آزمون t جفتی مناسب نباشد. به همین دلیل ویلکاکسون ابزاری بسیار ارزشمند برای تحلیل داده های واقعی در علوم اجتماعی، روانشناسی، پزشکی و سایر حوزه های پژوهشی به شمار می رود.

مزیت اصلی آزمون ویلکاکسون در این است که بر اساس رتبه ها کار می کند و به جای میانگین و واریانس، تغییرات و تفاوت های مشاهده شده را با روشی انعطاف پذیر تحلیل می نماید. این ویژگی باعث می شود نتایج آزمون در شرایطی که داده ها دارای انحراف از نرمال بودن هستند، همچنان معتبر باقی بماند. پژوهشگران با استفاده از این روش می توانند به شکلی دقیق تر و کاربردی تر فرضیه های خود را بررسی کنند و تصمیم های علمی یا عملی مطمئن تری بگیرند.

آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) یکی از مهم ترین و پرکاربرد ترین روش ها در آمار ناپارامتری است که برای تحلیل داده های جفتی و بررسی تفاوت میان آن ها به کار می رود. اهمیت این آزمون زمانی بیشتر می شود که داده های ما توزیع نرمال نداشته باشند و استفاده از آزمون های پارامتری مانند آزمون T امکان پذیر نباشد. در دنیای واقعی، بسیاری از داده ها در حوزه هایی مانند روانشناسی، علوم اجتماعی، پزشکی و حتی اقتصاد، شرایط نرمال بودن را برآورده نمی کنند و اینجاست که آزمون ویلکاکسون به کمک پژوهشگران می آید.

• تحلیل آماری

این آزمون به دلیل سادگی در محاسبات، انعطاف پذیری و قدرت بالا در تشخیص اختلاف های معنادار، جایگاه ویژه ای در تحقیقات علمی به دست آورده است. در این مقاله قصد داریم به صورت کامل و حرفه ای با ماهیت آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test)، انواع آن، مراحل محاسبه آماره، کاربرد های عملی و تفاوت آن با آزمون T آشنا شویم تا بتوانیم در تحلیل داده های خود بهترین استفاده را از این ابزار قدرتمند داشته باشیم.

• مشاوره آماری

آزمون رتبه ای ویلکاکسون چیست؟

آزمون ویلکاکسون یک آزمون آماری ناپارامتری می باشد که برای بررسی دو گروه جفتی استفاده می شود تا مشخص شود آیا تفاوت معنادار آماری بین آن ها وجود دارد یا خیر.

منظور از ناپارامتری این است که داده ها الزاما توزیع نرمال را نشان نمی دهند و نیازی به چنین فرضی برای تحلیل وجود ندارد. به همین دلیل آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) یکی از پرکاربرد ترین روش ها در آمار ناپارامتری محسوب می شود، زیرا در شرایطی که آزمون های پارامتری قابل استفاده نیستند، می تواند نتایج قابل اعتمادی ارائه دهد.

آزمون ویلکاکسون می تواند به دو نوع مختلف اشاره داشته باشد:

1. آزمون مجموع رتبه ها (Rank Sum Test)
2. آزمون رتبه ای علامت دار یا همان Signed-Rank Test

هر کدام از این دو نسخه در موقعیت های خاصی استفاده می شوند و محققان بسته به نوع داده های خود، نسخه مناسب را انتخاب می کنند.

• آزمون Z در آمار چیست؟

نکات کلیدی درباره آزمون ویلکاکسون

• آزمون ویلکاکسون در دو نسخه معرفی می شود: مجموع رتبه ها و رتبه ای علامت دار.
• هدف اصلی این آزمون آن است که بررسی کند آیا دو یا چند مجموعه داده جفتی با یکدیگر اختلاف معنادار آماری دارند یا خیر.
• هر دو نسخه این مدل فرض می کنند که داده ها از جوامع وابسته به دست آمده اند. به عبارت دیگر، داده ها به گونه ای هستند که مثلا تغییرات مربوط به یک فرد، یک گروه، یا حتی یک متغیر مانند قیمت سهام در طول زمان یا در شرایط مکانی مختلف دنبال می شود.

به همین دلیل آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) برای تحلیل داده هایی که ماهیت وابسته دارند، بسیار مناسب است و به محققان اجازه می دهد بدون نیاز به فرض نرمال بودن توزیع، به نتایج علمی دست پیدا کنند.

• آزمون F: تست F با فرمول، محاسبه و مثال دستی و اکسل

درک بهتر آزمون رتبه ای ویلکاکسون

آزمون مجموع رتبه ها و آزمون رتبه ای علامت دار نخستین بار توسط آمارشناس آمریکایی فرانک ویلکاکسون در یک مقاله پژوهشی تاثیرگذار در سال 1945 معرفی شدند. این دو روش نقش مهمی در پایه گذاری آزمون فرض آماری در حوزه آمار ناپارامتری ایفا کردند.

این آزمون ها برای تحلیل داده هایی به کار می روند که قابلیت رتبه بندی دارند اما لزوما مقدار عددی مشخصی ندارند. به عنوان مثال داده هایی مانند میزان رضایت مشتریان یا بررسی های مربوط به کیفیت موسیقی را می توان با کمک آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) مورد ارزیابی قرار داد.

توزیع های ناپارامتری بر خلاف توزیع های پارامتری، پارامتر های مشخصی ندارند و نمی توان آن ها را با یک معادله ریاضی ساده تعریف کرد. به همین دلیل این نوع آزمون ها انعطاف بیشتری در تحلیل داده هایی که از الگو های رایج پیروی نمی کنند، در اختیار پژوهشگران قرار می دهند.

• انواع داده ها در آمار

چه پرسش هایی با آزمون رتبه ای ویلکاکسون پاسخ داده می شود؟

آزمون رتبه ای ویلکاکسون می تواند در پاسخ به پرسش های متنوعی کاربرد داشته باشد، از جمله:

• آیا نمرات آزمون دانش آموزان از پایه پنجم به پایه ششم تغییر معناداری داشته است؟
• آیا یک داروی خاص در صورتی که روی یک گروه ثابت از افراد آزمایش شود، تاثیر قابل توجهی بر سلامت آن ها می گذارد؟

این مدل ها بر اساس این فرض طراحی شده اند که داده ها از دو جامعه وابسته یا هماهنگ به دست آمده اند. به عبارتی دیگر، داده ها مربوط به یک فرد مشخص، یک دارایی مالی مانند سهام یا یک پدیده خاص هستند که در طول زمان یا در مکان های متفاوت دنبال می شوند.

همچنین فرض می شود که داده ها پیوسته هستند، نه گسسته. از آنجایی که آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) یک آزمون ناپارامتری است، نیازی به پیروی متغیر وابسته از یک توزیع احتمال خاص وجود ندارد. این ویژگی باعث شده است که این روش در بسیاری از مطالعات علمی و کاربردی جایگاه ویژه ای پیدا کند.

• میانگین وزنی درصد خطای مطلق (WMAPE)

انواع آزمون های ویلکاکسون

1. آزمون مجموع رتبه های ویلکاکسون (Wilcoxon Rank Sum Test)

آزمون مجموع رتبه های ویلکاکسون برای بررسی فرض صفر به کار می رود. فرض صفر در اینجا بیان می کند که دو جامعه آماری دارای یک توزیع پیوسته مشابه هستند و تفاوت معناداری بین آن ها وجود ندارد.

به طور کلی فرض صفر در آمار به معنای این است که تفاوتی معنادار میان دو جامعه یا دو متغیر وجود ندارد و هر اختلاف مشاهده شده تنها ناشی از تصادف یا خطای نمونه گیری است.

برای اجرای آزمون مجموع رتبه های ویلکاکسون چند فرض اساسی باید برقرار باشد:

• داده ها از یک جامعه مشابه انتخاب شده باشند و جفتی باشند.
• داده ها باید حداقل در مقیاس فاصله ای (Interval Scale) قابل اندازه گیری باشند.
• داده ها به صورت تصادفی و مستقل انتخاب شده باشند.

این شرایط باعث می شوند تا نتایج آزمون معتبر بوده و بتوان آن را در تحلیل های علمی مورد استفاده قرار داد.

• سیستم غیر خطی شکار و شکارچی

2. آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test)

آزمون رتبه ای علامت دار یا همان Wilcoxon Signed-Rank Test بر این فرض استوار است که در اختلاف های بین مشاهدات جفتی، هم بزرگی اختلاف و هم علامت آن (مثبت یا منفی بودن) حاوی اطلاعات مهم هستند.

این آزمون به عنوان معادل ناپارامتری آزمون t زوجی (Paired Student’s t-test) شناخته می شود. در واقع، زمانی که داده های جامعه از توزیع نرمال پیروی نمی کنند یا شرایط لازم برای آزمون t فراهم نیست، می توان از آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) به عنوان جایگزینی مطمئن استفاده کرد.

این ویژگی باعث شده است که آزمون ویلکاکسون یکی از پرکاربردترین ابزارها در تحلیل های آماری به ویژه در علوم اجتماعی، روانشناسی، پزشکی و حتی بازارهای مالی باشد. زیرا در بسیاری از مواقع داده های واقعی توزیع نرمال ندارند و نیاز به آزمون های ناپارامتری مانند این روش احساس می شود.

• آشنایی کامل با نرم افزار ایویوز (EViews)

محاسبه آماره آزمون ویلکاکسون

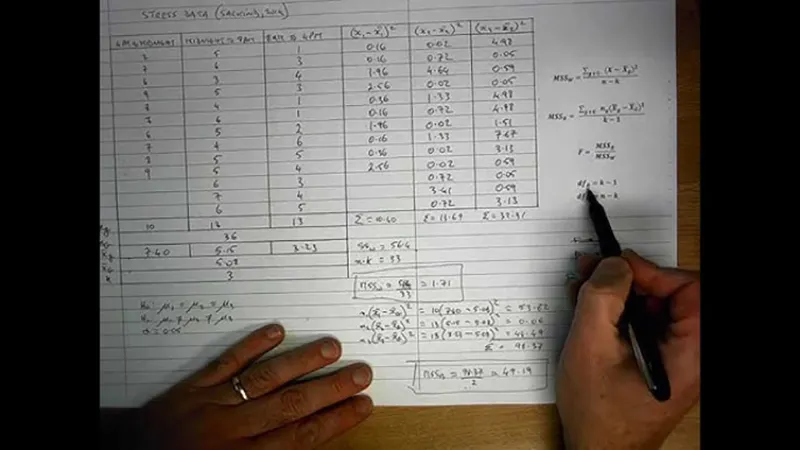
مراحل به دست آوردن آماره آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) که با نماد W نشان داده می شود به شرح زیر است:

1. محاسبه اختلاف ها: برای هر داده در یک نمونه شامل n مشاهده، یک نمره اختلاف بین دو اندازه گیری محاسبه می شود. به عبارت دیگر، یکی از مقادیر از دیگری کسر می گردد.
2. قدر مطلق اختلاف ها: پس از محاسبه اختلاف ها، علامت مثبت یا منفی کنار گذاشته می شود و مجموعه ای از قدر مطلق اختلاف ها ∣∣ به دست می آید.
3. حذف اختلاف های صفر: اختلاف هایی که مقدارشان صفر است کنار گذاشته می شوند. بنابراین یک مجموعه از اختلاف های غیر صفر باقی می ماند که تعداد آن ها را با n′ نمایش می دهند و این n′ در عمل به عنوان حجم نمونه واقعی در نظر گرفته می شود.
4. اختصاص رتبه ها: به هر یک از اختلاف های غیر صفر، رتبه ای بین 1 تا n داده می شود. کوچک ترین اختلاف مطلق رتبه 1 و بزرگ ترین اختلاف مطلق رتبه n را دریافت می کند. در صورتی که دو یا چند مقدار ||با هم برابر باشند، به هر یک میانگین رتبه هایی که در حالت عادی دریافت می کردند اختصاص داده می شود.
5. اختصاص علامت به رتبه ها: در این مرحله دوباره به هر رتبه علامت مثبت یا منفی داده می شود بر اساس این که مقدار اولیه مثبت بوده یا منفی.
6. محاسبه آماره :W در نهایت آماره آزمون ویلکاکسون W برابر است با مجموع رتبه های مثبت.

در عمل، انجام دستی این محاسبات زمان بر و مستعد خطا می باشد. به همین دلیل در تحقیقات علمی، محققان معمولا از نرم افزارهای تحلیل آماری یا حتی صفحات گسترده مانند اکسل برای محاسبه آماره آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) استفاده می کنند. این ابزارها محاسبات را ساده تر کرده و احتمال خطای انسانی را کاهش می دهند.

• آزمون های آماری در R با جزئیات

آزمون رتبه ای ویلکاکسون برای چه مواردی استفاده می شود؟

آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) برای مقایسه دو نمونه مرتبط یا بررسی تفاوت در چندین اندازه گیری از یک نمونه واحد به کار می رود. هدف اصلی این آزمون آن است که مشخص کند آیا بین دو مجموعه داده وابسته تفاوتی وجود دارد و اگر چنین تفاوتی مشاهده شود، آیا این اختلاف واقعا معنادار است یا تنها نتیجه شانس و تصادف می باشد.

به عبارت دیگر، این آزمون به ما کمک می کند تا بررسی کنیم آیا تغییرات میانگین رتبه های جامعه در دو شرایط مختلف واقعی هستند یا خیر. همین موضوع باعث شده است که آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) در علوم اجتماعی، روانشناسی، پزشکی و حتی مطالعات مالی و اقتصادی جایگاه ویژه ای داشته باشد.

• آنالیز کواریانس

آزمون T چیست؟

همانند آزمون ویلکاکسون، آزمون T نیز ابزاری آماری برای بررسی وجود یا عدم وجود تفاوت معنادار میان دو نمونه وابسته می باشد. تفاوت اصلی در این است که آزمون T معمولا زمانی به کار می رود که داده ها توزیع نرمال داشته باشند و واریانس داده ها ناشناخته باشد.

• آزمون تی (T-test)

برای اجرای آزمون T باید چند فرض اساسی برقرار باشد؛ از جمله فرض نرمال بودن داده ها. در غیر این صورت، نتایج آزمون T قابل اعتماد نخواهند بود.

چرا استفاده از آزمون رتبه ای ویلکاکسون به جای آزمون T؟

از آنجا که آزمون T نیازمند برقرار بودن چندین فرض آماری است، در شرایطی که این فرض ها برقرار نباشند، استفاده از آزمون T درست نخواهد بود. در چنین مواردی، پژوهشگران به سراغ آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) می روند.

به عنوان مثال، اگر داده ها از توزیع نرمال پیروی نکنند، آزمون T دیگر معتبر نیست. در این شرایط استفاده از آزمون ویلکاکسون بهترین جایگزین خواهد بود، زیرا این آزمون نیازی به فرض نرمال بودن داده ها ندارد و می تواند در تحلیل داده های ناپارامتری نتایج دقیقی ارائه دهد.

این انعطاف پذیری یکی از دلایل اصلی محبوبیت آزمون رتبه ای ویلکاکسون در تحقیقات می باشد، چرا که بسیاری از داده های واقعی در حوزه های مختلف علمی و عملی از توزیع نرمال پیروی نمی کنند.

• آزمون t تک نمونه ای چیست؟

جمع بندی

به طور خلاصه، آزمون رتبه ای ویلکاکسون (Wilcoxon Signed-Rank Test) ابزاری قدرتمند در آمار ناپارامتری است که زمانی به کار می رود که آزمون های کلاسیک مانند آزمون T پاسخگو نباشند. این آزمون با بررسی داده های جفتی و تحلیل رتبه ها، امکان کشف تفاوت های معنادار را فراهم می کند. انعطاف پذیری، دقت و کاربرد گسترده آن در رشته های مختلف نشان می دهد که پژوهشگران برای رسیدن به نتایج معتبر و علمی، همواره باید این آزمون را به عنوان یکی از انتخاب های اصلی خود در نظر داشته باشند.