آزمون کروسکال والیس (Kruskal-Wallis test)

چکیده مقاله:
آزمون کروسکال والیس یکی از آزمون های ناپارامتریک است که برای مقایسه بیش از دو گروه مستقل به کار می رود. این آزمون زمانی مورد استفاده قرار می گیرد که داده ها الزامات آزمون های پارامتریک مانند نرمال بودن توزیع یا برابری واریانس ها را برآورده نمی کنند. اساس آزمون کروسکال والیس بر رتبه بندی داده ها استوار است و به جای استفاده از مقادیر خام، داده ها ابتدا رتبه بندی می شوند و سپس میانگین رتبه ها در گروه های مختلف با هم مقایسه می شوند. این ویژگی باعث می شود آزمون نسبت به انحراف از نرمال بودن یا وجود داده های پرت مقاوم تر باشد.
از آزمون کروسکال والیس معمولا در پژوهش های علوم اجتماعی، پزشکی و علوم رفتاری استفاده می شود، جايي که داده ها اغلب به صورت رتبه ای یا غیر نرمال جمع آوری می شوند. این آزمون تعمیمی از آزمون من ویتنی یو (Mann-Whitney U test) برای بیش از دو گروه است. نتیجه آزمون نشان می دهد که آیا تفاوت معناداری بین گروه ها از نظر توزیع رتبه ها وجود دارد یا خیر، اما مشخص نمی کند کدام گروه ها با یکدیگر متفاوت هستند. در صورت معنادار بودن نتیجه، برای شناسایی دقیق تفاوت ها از آزمون های تعقیبی ناپارامتریک استفاده می شود.
آزمون کروسکال والیس (Kruskal-Wallis test) یکی از مهم ترین و کاربردی ترین آزمون های ناپارامتری برای مقایسه چند گروه مستقل است. این آزمون زمانی استفاده می شود که داده ها نرمال نباشند یا واریانس بین گروه ها یکسان نباشد. آزمون کروسکال والیس به محققان امکان می دهد تا میانگین رتبه ها را میان گروه های مختلف مقایسه کنند و بررسی کنند که آیا تفاوت معنی داری وجود دارد یا خیر. در این مقاله، نحوه محاسبه، تفسیر و گزارش نتایج آزمون کروسکال والیس به صورت گام به گام توضیح داده می شود. همچنین مثال هایی کاربردی و نکات کلیدی برای تحلیل داده ها ارائه خواهد شد تا خواننده بتواند به راحتی این آزمون را در تحقیقات خود به کار ببرد.

آزمون کروسکال والیس چیست؟
آزمون کروسکال والیس که گاهی با نام H test هم شناخته می شود یک آزمون آماری ناپارامتری است که برای مقایسه سه یا چند گروه مستقل به کار می رود تا مشخص شود آیا بین این گروه ها اختلاف معنادار آماری وجود دارد یا خیر. در واقع این آزمون را می توان نسخه توسعه یافته آزمون Mann-Whitney U دانست که تنها برای مقایسه دو گروه طراحی شده است.
اهمیت آزمون کروسکال والیس در این است که برخلاف آزمون های پارامتری، وابسته به توزیع نرمال داده ها نیست. در بسیاری از پژوهش های علمی، داده ها شرایط لازم برای اجرای آزمون های پارامتری مانند آنالیز واریانس (ANOVA) را ندارند. در چنین شرایطی استفاده از روش های ناپارامتری مثل آزمون کراسکال والیس، بهترین انتخاب خواهد بود.
از نظر فلسفه آماری، آزمون کروسکال والیس مبتنی بر رتبه داده ها عمل می کند. به جای استفاده از میانگین خام، داده ها رتبه بندی می شوند و سپس مقایسه بین گروه ها انجام می گیرد. این ویژگی باعث می شود آزمون نسبت به داده های پرت و نرمال نبودن توزیع مقاوم تر باشد.
آزمون کروسکال والیس زمانی به کار گرفته می شود که پیش فرض های لازم برای انجام تحلیل واریانس یک طرفه (One-way ANOVA) برقرار نباشند. همانطور که می دانیم، روش های پارامتری مانند ANOVA به شدت وابسته به مفروضاتی مثل نرمال بودن توزیع داده ها و برابری واریانس ها هستند. اگر داده ها این شرایط را نداشته باشند، استفاده از آزمون های پارامتری می تواند منجر به نتایج گمراه کننده شود.
در چنین شرایطی، آزمون کروسکال والیس به عنوان یک آزمون ناپارامتری جایگزین بسیار مناسب خواهد بود. دلیل آن این است که این آزمون به هیچ وجه نیازمند توزیع نرمال نیست و محقق می تواند با داده هایی که پراکندگی یا توزیع نامتقارن دارند نیز به راحتی کار کند.
تنها شرط اصلی برای اجرای آزمون این است که داده ها در مقیاس ترتیبی (Ordinal Scale) باشند. به این معنا که محقق باید بتواند داده ها را به صورت رتبه بندی شده مورد مقایسه قرار دهد. در این مقیاس، ترتیب داده ها اهمیت دارد اما فاصله دقیق بین مقادیر اندازه گیری نمی شود. برای مثال، رضایت مشتریان از یک محصول می تواند در قالب رتبه های “کم”، “متوسط” و “زیاد” اندازه گیری شود. چنین داده هایی به راحتی با استفاده از آاین آزمون تحلیل می شوند.
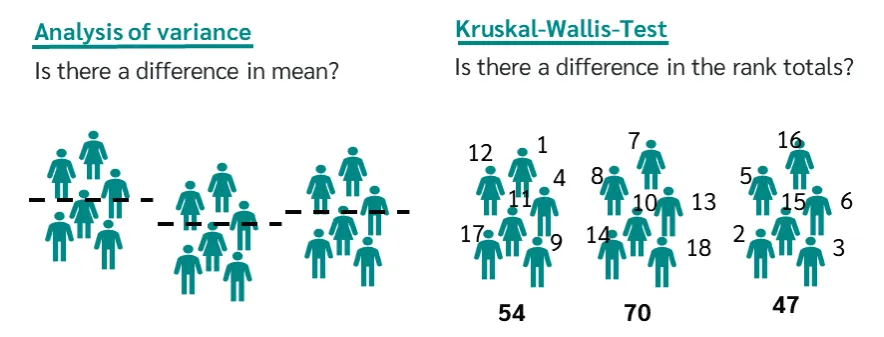
ویژگی های اصلی آزمون کروسکال والیس
-
ناپارامتری بودن
این آزمون هیچ فرضی درباره نرمال بودن توزیع داده ها ندارد، به همین دلیل برای داده هایی که به شکل نرمال توزیع نشده اند گزینه بسیار مناسبی محسوب می شود. پژوهشگران در بسیاری از مطالعات تجربی با داده هایی مواجه می شوند که پراکندگی یا عدم تقارن زیادی دارند. در چنین مواردی آزمون کروسکال می تواند نتایج معتبرتری نسبت به روش های پارامتری ارائه دهد.
-
کاربرد در داده های ترتیبی یا پیوسته رتبه بندی شده
این آزمون هم برای داده های ترتیبی و هم برای داده های پیوسته که به رتبه تبدیل شده اند کاربرد دارد. مثلا اگر در یک تحقیق میزان رضایت بیماران از یک روش درمانی به صورت “کم”، “متوسط” و “زیاد” ثبت شود، می توان این داده ها را رتبه بندی کرد و از این آزمون استفاده نمود. همچنین در پژوهش هایی که داده ها کمی هستند اما نیاز به مقایسه بین چند گروه وجود دارد، این روش بسیار کاربردی خواهد بود.
-
گروه های مستقل
یکی دیگر از ویژگی های کلیدی این است که برای مقایسه گروه های مستقل به کار می رود. منظور از گروه های مستقل این است که مشاهدات هر گروه ارتباطی با گروه دیگر نداشته باشند. برای مثال، مقایسه عملکرد سه کلاس مختلف دانش آموزان در یک آزمون آموزشی را می توان با این آزمون انجام داد، زیرا هیچ دانش آموزی در دو کلاس حضور ندارد و داده ها از هم مستقل هستند.
این ویژگی ها موجب شده اند که آزمون کروسکال والیس به یکی از پرکاربردترین روش های ناپارامتری در تحلیل داده ها تبدیل شود و در حوزه های مختلف علمی و تحقیقاتی جایگاه ویژه ای پیدا کند.
مثال هایی برای آزمون کروسکال والیس
-
مثال پزشکی:
فرض کنید یک شرکت داروسازی قصد دارد بررسی کند که آیا داروی XY بر وزن بدن افراد تاثیر دارد یا خیر. برای این منظور، دارو به 20 فرد داوطلب داده می شود، 20 فرد دیگر دارونما (Placebo) دریافت می کنند و 20 فرد هم بدون دارو یا دارونما باقی می مانند. در این تحقیق سه گروه مستقل وجود دارد و داده ها ممکن است از نظر آماری توزیع نرمال نداشته باشند. در چنین حالتی، به جای استفاده از تحلیل واریانس، پژوهشگر می تواند از این آزمون استفاده کند تا مشخص شود آیا بین این سه گروه تفاوت معناداری در تغییرات وزن بدن وجود دارد یا خیر.
-
مثال علوم اجتماعی:
در حوزه علوم اجتماعی، یک محقق ممکن است به دنبال بررسی این موضوع باشد که آیا میزان تماشای تلویزیون در میان سه گروه سنی مختلف تفاوت دارد یا خیر. برای نمونه، گروه اول شامل افراد 18 تا 30 سال، گروه دوم شامل افراد 31 تا 50 سال و گروه سوم شامل افراد بالای 50 سال باشند. داده های مربوط به ساعت های تماشای تلویزیون ممکن است نرمال توزیع نشده باشند یا شامل مقادیر پرت باشند. در اینجا آزمون کروسکال والیس بهترین گزینه است، زیرا می تواند بر اساس رتبه داده ها تفاوت بین گروه ها را بررسی کند و به محقق پاسخ دقیقی بدهد.
این مثال ها نشان می دهند که این آزمون چقدر در حوزه های مختلف از پزشکی تا علوم اجتماعی کاربرد دارد. هر جا که داده ها نرمال نباشند یا تنها به صورت رتبه ای گردآوری شوند، این آزمون می تواند ابزاری قابل اعتماد و علمی برای تحلیل باشد.
پرسش پژوهش و فرضیات
در آزمون کروسکال والیس، پرسش اصلی پژوهش می تواند این باشد: آیا بین گرایش مرکزی چند نمونه مستقل تفاوت وجود دارد؟ پاسخ به این پرسش منجر به تدوین فرضیه صفر و فرضیه جایگزین می شود.
- فرضیه صفر (H0): نمونه های مستقل همگی دارای گرایش مرکزی یکسان هستند و بنابراین از یک جامعه آماری مشترک سرچشمه گرفته اند.
- فرضیه جایگزین (H1): حداقل یکی از نمونه های مستقل دارای گرایش مرکزی متفاوت با دیگر نمونه ها است و بنابراین از جامعه ای متفاوت منشا می گیرد.
این ساختار فرضیه ای به پژوهشگر کمک می کند تا به صورت آماری بررسی کند که آیا تفاوت مشاهده شده بین گروه ها ناشی از تصادف است یا نشان دهنده یک الگوی واقعی در داده ها می باشد.
میانه در برابر مجموع رتبه ها
نکته مهمی که باید روشن شود این است که آزمون کروسکال والیس در واقع اختلاف بین مجموع رتبه های گروه ها را بررسی می کند، نه مستقیما اختلاف میانه ها را. این تمایز ظریف اما مهم است.
- مجموع رتبه ها:
در این آزمون، تمام داده های همه گروه ها با هم ترکیب می شوند و هر مقدار با رتبه اش در کل مجموعه داده جایگزین می گردد. سپس برای هر گروه، مجموع رتبه ها محاسبه می شود. فرضیه صفر بیان می کند که میانگین رتبه های گروه ها با هم برابر است. بنابراین آزمون اساسا به مقایسه رتبه ها می پردازد.
- میانه:
با اینکه در عمل، آزمون کروسکال والیس اغلب به عنوان شاخصی از تفاوت در میانه ها به کار می رود (به ویژه زمانی که توزیع داده ها در گروه ها مشابه باشد)، اما به صورت مستقیم میانه ها را بررسی نمی کند. دلیل این برداشت این است که اگر توزیع ها مشابه باشند، اختلاف در میانگین رتبه ها به احتمال زیاد نشان دهنده اختلاف در میانه ها نیز خواهد بود.
این نکته بسیار حائز اهمیت است، چرا که بسیاری از محققان ممکن است تصور کنند این آزمون صرفا تفاوت در میانه ها را بررسی می کند، در حالی که در واقع این آزمون بر اساس رتبه ها عمل می نماید.
به طور خلاصه، آزمون کروسکال یک روش ناپارامتری برای بررسی این موضوع است که آیا نمونه ها از یک توزیع مشترک منشا گرفته اند یا خیر. این آزمون بررسی می کند که آیا میانگین رتبه ها در بین گروه ها برابر هستند یا نه. در عمل، این موضوع اغلب به عنوان آزمونی برای شناسایی تفاوت در میانه ها تفسیر می شود، به ویژه زمانی که شکل توزیع داده ها در گروه های مختلف مشابه باشد.
این ویژگی باعث شده است که این تست به ابزاری بسیار ارزشمند در تحلیل داده های رتبه ای یا غیر نرمال تبدیل شود و جایگاه ویژه ای در تحقیقات علمی به دست آورد.
مفروضات تست کروسکال والیس
برای محاسبه و اجرای این تست تنها چند شرط ساده لازم است. نخست اینکه باید چندین نمونه تصادفی و مستقل در اختیار داشته باشیم. این نمونه ها باید حداقل دارای ویژگی هایی در سطح مقیاس ترتیبی (Ordinal Scale) باشند. به عبارت دیگر، داده ها باید حداقل قابلیت رتبه بندی داشته باشند.
نکته مهم دیگر این است که در این تست، متغیرها الزامی به پیروی از یک توزیع خاص یا قرار گرفتن روی منحنی نرمال ندارند. این ویژگی دقیقا همان چیزی است که آزمون را از روش های پارامتری متمایز می کند. در حالی که بسیاری از آزمون های آماری کلاسیک مانند تحلیل واریانس یا آزمون t به شدت وابسته به فرض نرمال بودن داده ها هستند، تست کروسکال والیس با حذف این پیش فرض، آزادی عمل بسیار بیشتری به پژوهشگر می دهد.
به طور خلاصه، مفروضات اصلی برای اجرای این تست عبارتند از:
- وجود چند نمونه مستقل (گروه ها نباید همپوشانی داشته باشند).
- داده ها حداقل در سطح ترتیبی باشند تا امکان رتبه بندی فراهم شود.
- نیاز به پیروی از توزیع نرمال یا هر گونه منحنی خاص وجود ندارد.
این سادگی در مفروضات یکی از دلایل اصلی محبوبیت این تست در تحقیقات است. پژوهشگرانی که با داده های غیر نرمال، رتبه ای یا حتی داده های کوچک سروکار دارند می توانند بدون نگرانی از نقض فرضیات سختگیرانه، از این آزمون استفاده کنند.
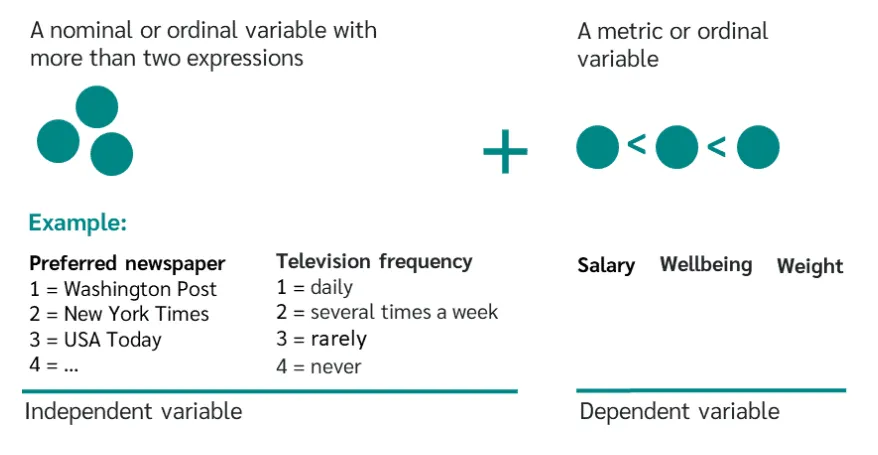
نمونهای از متغیر های مستقل (اسمی یا ترتیبی تصویر سمت چپ) و متغیر های وابسته (متریک یا ترتیبی، تصویر سمت راست) در تحلیل آماری
محاسبه تست کروسکال والیس (Kruskal-Wallis test)
محاسبه تحلیل واریانس رتبه ای کروسکال والیس مشابه آزمون من-ویتنی U می باشد. آزمون من-ویتنی U در واقع همتای ناپارامتری آزمون t برای نمونه های مستقل است و زمانی به کار می رود که فرض نرمال بودن داده ها برقرار نباشد. Kruskal-Wallis test نیز در همین دسته از آزمون های ناپارامتری قرار می گیرد و برای مقایسه چند گروه مستقل مورد استفاده قرار می گیرد.
حال فرض کنید فرض صفر برقرار باشد. این یعنی بین نمونه های مستقل تفاوتی وجود ندارد. در چنین حالتی، رتبه های بالا و پایین به صورت تصادفی در میان نمونه ها توزیع می شوند و باید به طور مساوی در گروه ها پخش شوند. به عبارت دیگر، احتمال اینکه یک رتبه به یک گروه خاص اختصاص پیدا کند برای تمام گروه ها یکسان خواهد بود.
اگر واقعا تفاوتی میان گروه ها وجود نداشته باشد، مقدار میانگین رتبه ها نیز باید در تمامی گروه ها برابر باشد. در نتیجه، مقدار مورد انتظار رتبه ها برای هر گروه برابر خواهد بود. این ویژگی به ما کمک می کند تا درک کنیم اساس Kruskal-Wallis test بر مقایسه میانگین رتبه ها میان چند گروه مستقل بنا شده است.

هر نمونه دارای مقدار مورد انتظار یکسانی از رتبه ها می باشد که این مقدار با مقدار مورد انتظار جامعه آماری متناظر است. علاوه بر این، برای انجام آزمون، واریانس رتبه ها نیز مورد نیاز است. واریانس رتبه ها را می توان با استفاده از فرمول زیر محاسبه کرد:
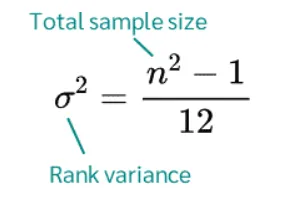
در آزمون کروسکال والیس، متغیر آزمون H محاسبه می شود. مقدار H با مقدار χ² متناظر است و نشان دهنده شدت تفاوت میان گروه ها می باشد.
مقدار H از رابطه زیر حاصل می شود:
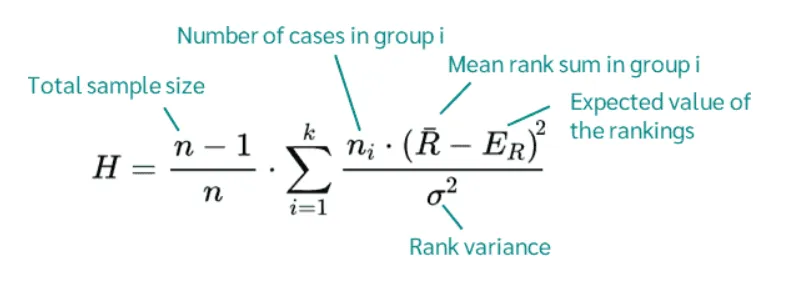
مقدار بحرانی H را می توان از جدول مقادیر بحرانی χ² استخراج کرد. این مقدار به ما کمک می کند تا تصمیم بگیریم که آیا تفاوت میان گروه ها معنی دار است یا خیر. اگر مقدار H محاسبه شده بزرگتر از مقدار بحرانی جدول باشد، فرض صفر رد می شود و نتیجه می گیریم که بین حداقل دو گروه تفاوت وجود دارد.
آزمون پس از انجام آزمون اصلی (Post-hoc Test)
Kruskal-Wallis test می تواند مشخص کند که حداقل دو گروه با یکدیگر تفاوت دارند، اما به تنهایی پاسخ نمی دهد که کدام گروه ها با یکدیگر متفاوت هستند. برای تعیین این موضوع، نیاز به انجام یک آزمون پس از آزمون اصلی یا Post-hoc test وجود دارد.
برای این منظور، آزمون دان (Dunn test) به عنوان یک آزمون ناپارامتری مناسب برای مقایسه زوجی چند گروه استفاده می شود. این آزمون به محققان کمک می کند تا اختلاف بین هر جفت گروه را به صورت جداگانه بررسی کنند و مقدار p مربوط به هر مقایسه را محاسبه کنند.
آزمون Dunn-Bonferroni
برای تشخیص اینکه کدام جفت گروه ها با یکدیگر تفاوت دارند، گروه های فردی را می توان به صورت زوجی مقایسه کرد. آزمون دان برای محاسبه مقدار p هر جفت گروه به کار می رود. به عنوان مثال، برای مقایسه گروه A و B، مقدار z با استفاده از فرمول زیر محاسبه می شود:
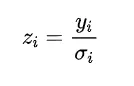
محاسبه مقدار z برای مقایسه گروه A و B
که در آن i یکی از گروه ها می باشد و تفاوت مجموع میانگین رتبه ها بین دو گروه است. خطای استاندارد نیز به صورت زیر محاسبه می شود:
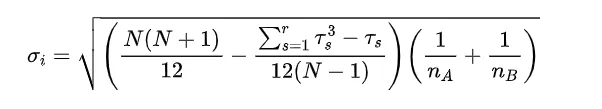
فرمول محاسبه خطای استاندارد که در آن N تعداد کل نمونه ها، r تعداد رتبه های مرتبط و τs تعداد نمونه ها در آن رتبه می باشد.
مقدار p محاسبه شده سپس می تواند با استفاده از تصحیح بونفرونی (Bonferroni correction) تنظیم شود. تصحیح بونفرونی ساده ترین روش برای مقابله با مشکل مقایسه های چندگانه است. در این روش، مقدار p محاسبه شده در هر مقایسه، در تعداد گروه ها ضرب می شود.
اگر مقدار p تعدیل شده در یک مقایسه زوجی کمتر از سطح معنی داری (معمولاً 0.05) باشد، فرض صفر که بیان می کند هیچ تفاوتی وجود ندارد، رد می شود. بنابراین، اگر مقدار p تعدیل شده کمتر از 0.05 باشد، فرض می گردد که دو گروه مورد نظر با یکدیگر متفاوت هستند.
برنامه DATAtab به طور خودکار آزمون Dunn-Bonferroni را هنگام محاسبه تست Kruskal-Wallis ارائه می دهد و به محققان کمک می کند تا به راحتی تفاوت های زوجی میان گروه ها را تحلیل کنند.
جمع بندی
آزمون کروسکال والیس ابزاری قدرتمند برای تحلیل داده های ناپارامتری و مقایسه چند گروه مستقل است. با استفاده از این آزمون، می توان تفاوت میانگین رتبه ها را بررسی کرد و تصمیم گرفت که آیا فرض صفر قابل رد است یا خیر. مقدار H و مقدار p دو شاخص اصلی برای تفسیر نتایج این آزمون می باشند. نتایج آزمون باید به صورت دقیق و با ذکر مقادیر محاسبه شده و سطح معنی داری گزارش شوند. در نهایت، این آزمون کمک می کند تا تحلیل آماری داده های پیچیده به شکل ساده و علمی انجام شود و تصمیم گیری بر اساس شواهد آماری دقیق صورت گیرد.
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











