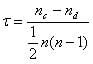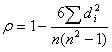انواع ضرایب همبستگی

چکیده مقاله :
یکی دیگر از مباحث مهم در آنالیز و تحلیل آماری ضرایب همبستگی می باشد. با استفاده از ضرایب همبستگی مختلف باتوجه به شرایط مسئله می توان تحلیل های متفاوت و ارزشمندی را استخراج کرد. در این مقاله انواع ضرایب همبستگی ازجمله کواریانس ، پیرسون ، کندال ، اسپیرمن و پلیکریک را معرفی و به بررسی هریک باتوجه به نوع مسئله ای که در آن کاربرد دارند ، مفروضات لازم و نوع تحلیل حاصل از نتایج آن ها را توضیح می دهیم.
1- ضرایب همبستگی (کواریانس ، پیرسون ، کندال ، اسپیرمن)
همبستگی یک تحلیل دو متغیره است که قدرت ارتباط بین دو متغیر و جهت رابطه را اندازه گیری می کند. از نظر قدرت رابطه، مقدار ضریب همبستگی بین +1 و -1 متغیر است. مقدار 1± درجه ارتباط بین دو متغیر را نشان می دهد. با رفتن مقدار ضریب همبستگی به سمت 0، رابطه بین دو متغیر ضعیف تر خواهد بود. جهت رابطه با علامت ضریب نشان داده می شود. علامت + نشان دهنده رابطه مثبت و علامت – نشان دهنده رابطه منفی است. معمولاً در آمار، چهار نوع همبستگی را اندازه گیری می کنیم: همبستگی پیرسون، همبستگی رتبه کندال، همبستگی کواریانس، همبستگی اسپیرمن و همبستگی Point-Biserial. نرم افزار زیر به شما این امکان را می دهد که به راحتی یک همبستگی را انجام دهید.
در یک مجموعه داده موجود، بسیار مهم است که بتوانیم نوع مناسب ضریب همبستگی را تشخیص دهیم تا تصمیم بگیریم که آیا متغیر را در تحلیلها و مراحل مدلسازی آتی در مجموعه داده خود نگه داریم یا نه. در داده ها، ویژگی ها ممکن است رابطه فزاینده (مثبت) یا کاهشی (منفی) بین آنها همانطور که در زیر نشان داده شده است داشته باشند.
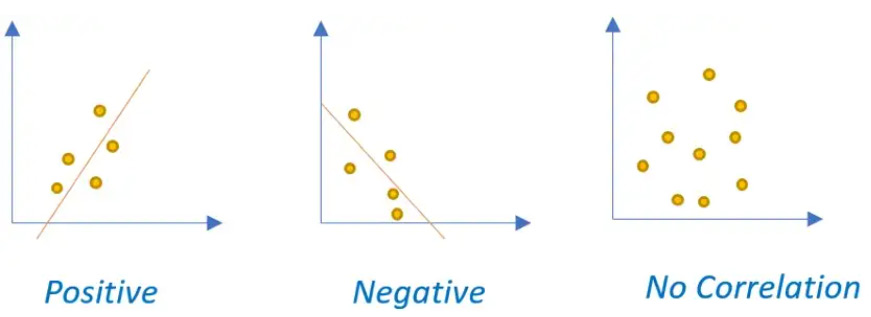
جهت ضرایب همبستگی
هر ضریب همبستگی با استفاده از حوزهها و جنبههای کاربرد آن، توصیف بسیار منحصر به فردی دارد. در این مقاله، چهار ضریب همبستگی اصلی مانند کوواریانس، پیرسون اسپیرمن ، ضریب همبستگی Polychoric و kendal را توضیح خواهیم داد.
جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تحلیل آماری چیست مطالعه نمایید.
2- ضریب همبستگی کوواریانس
به طور اساسی، همبستگی کوواریانس را می توان زمانی اعمال کرد که یک رابطه معمولی توزیع شده بین ویژگی ها وجود داشته باشد. به راحتی می توان از آن برای ارزیابی مجموع واریانس دو ویژگی خاص استفاده کرد. با استفاده از این ضریب می توان جهت ویژگی ها را فرض کرد. با این حال، در نیاز به اندازه گیری وابستگی متغیرها، یک متریک اضافی باید انتخاب شود زیرا ضریب کوواریانس نمی تواند به این رابطه پاسخ دهد. به زبان ساده، فرمول همبستگی کوواریانس را می توان در زیر یافت.
Covariance(X, Y) = (sum (x – mean(X)) * (y – mean(Y)) ) * 1/(n-1)
3- ضریب همبستگی پیرسون
برای همبستگی پیرسون، نیاز به یک رابطه خطی بین یک جفت متغیر نیز وجود دارد. در ادبیات، می توان آن را «Pearson product-moment correlation» نامید. فرمول همبستگی پیرسون را می توان از فرمول ریاضی همبستگی کوواریانس تولید کرد.
Pearson(X, Y) = Covariance(X, Y) / (stdDev(X) * stdDev(Y))
پارامتر ضریب همبستگی پیرسون ممکن است در پنج محدوده مختلف با توجه به موقعیت فعلی متغیرها در محور x و y مشاهده شود، دامنه همبستگی ممکن است تغییر کند.
هنگامی که نقاط داده از یک روند نزولی پیروی می کنند، می توان آن را به عنوان یک همبستگی منفی پذیرفت. از سوی دیگر، هنگامی که روند صعودی مشاهده می شود، می توان آن را به عنوان یک همبستگی مثبت بین دو متغیر مقایسه شده برچسب گذاری کرد. در تصویر زیر، p را می توان به عنوان ضریب همبستگی پذیرفت. شما می توانید ترازهای همبستگی را با توجه به توزیع نقاط داده بررسی کنید.
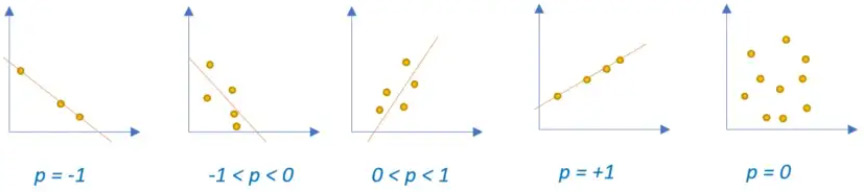
مقادیر متغیر ضریب همبستگی پیرسون
همبستگی پیرسون پرکاربردترین ضریب همبستگی آمار برای سنجش میزان رابطه بین متغیرهای مرتبط خطی است. به عنوان مثال، در بازار سهام، اگر بخواهیم ارتباط دو سهم را با یکدیگر اندازه گیری کنیم، از همبستگی پیرسون r برای اندازه گیری میزان ارتباط بین این دو استفاده می شود. همبستگی point-biserial با فرمول همبستگی پیرسون انجام می شود با این تفاوت که یکی از متغیرها دوگانه است. برای محاسبه همبستگی پیرسون r از فرمول زیر استفاده می شود:
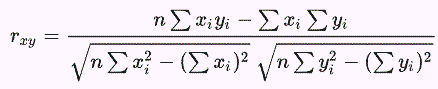
rxy = ضریب همبستگی پیرسون r بین x و y
n = تعداد مشاهدات
xi = مقدار x (برای مشاهده iام)
yi = مقدار y (برای مشاهده iام)
1-3- انواع مسائل تحقیقی که همبستگی پیرسون می تواند بررسی کند
آیا بین سن که بر حسب سال اندازه گیری می شود و قد بر حسب اینچ رابطه آماری معنی داری وجود دارد؟
آیا رابطه ای بین دمای اندازه گیری شده بر حسب درجه فارنهایت، و فروش بستنی محاسبه شده با درآمد ارتباطی وجود دارد؟
آیا بین رضایت شغلی که توسط JSS اندازهگیری میشود و درآمد که بر حسب دلار اندازهگیری میشود رابطه وجود دارد؟
2-3- مفروضات
برای همبستگی پیرسون r، هر دو متغیر باید به طور نرمال توزیع شوند. سایر مفروضات عبارتند از خطی بودن و همسانی. خطی بودن، یک رابطه خطی مستقیم بین هر یک از دو متغیر را فرض میکند و همسانی فرض میکند که دادهها به طور مساوی حول خط رگرسیون توزیع شدهاند.
3-3- کلمات کلیدی
اندازه اثر: استاندارد کوهن ممکن است برای ارزیابی ضریب همبستگی برای تعیین قدرت رابطه یا اندازه اثر استفاده شود. ضرایب همبستگی بین 0.10 و 0.29 نشان دهنده یک ارتباط کوچک، ضرایب بین 0.30 و 0.49 نشان دهنده یک ارتباط متوسط، و ضرایب 0.50 و بالاتر نشان دهنده یک ارتباط یا رابطه بزرگ است.
داده های پیوسته: داده هایی که سطح بازه یا نسبت هستند. این نوع داده دارای خواص بزرگی و فواصل مساوی بین واحدهای مجاور است. فواصل مساوی بین واحدهای مجاور به این معنی است که مقادیر مساوی از متغیر در حال اندازه گیری بین واحدهای مجاور در مقیاس وجود دارد. یک مثال می تواند سن باشد. افزایش سن از 21 به 22 با افزایش سن از 60 به 61 سال برابر است.
4- ضریب همبستگی کندال
همبستگی رتبه کندال یک آزمون ناپارامتریک است که قدرت وابستگی بین دو متغیر را اندازه گیری می کند. اگر دو نمونه a و b را در نظر بگیریم که هر کدام دارای n نمونه است، می دانیم که تعداد کل جفت ها با a b برابر با n(n-1)/2 است. برای محاسبه مقدار همبستگی رتبه کندال از فرمول زیر استفاده می شود:
Nc= تعداد همخوان
Nd= تعداد ناسازگار
5- ضریب همبستگی اسپیرمن
ضریب همبستگی اسپیرمن که میتوان آن را «Spearman’s Rank-Order Correlation» در محیط دانشگاهی نیز نامید، در موارد عدم وجود ماهیت توزیع نرمال در مجموعه متغیر اعمال میشود. فرمول همبستگی اسپیرمن نیز ممکن است از فرمول همبستگی کوواریانس با افزودن رتبه بندی متغیرها به فرمول استخراج شود. رتبهبندی را میتوان بهعنوان تعیین ترتیب برچسبهای متغیرها برای محاسبه سطح مطابقت بین زوج مشاهده خلاصه کرد که ممکن است برای ارزیابی میزان تأثیر آنها بر یکدیگر استفاده شود.
Spearman(X, Y) = Covariance(rank(X), rank(Y)) / (stdDev(rank(X)) * stdDev(rank(Y)))

مجموعه داده های توزیع شده Non-Gaussian
همبستگی رتبه اسپیرمن یک آزمون ناپارامتریک است که برای اندازه گیری میزان ارتباط بین دو متغیر استفاده می شود. آزمون همبستگی رتبه اسپیرمن هیچ فرضی در مورد توزیع داده ها ندارد و زمانی که متغیرها در مقیاسی اندازه گیری شوند که حداقل ترتیبی باشد، تحلیل همبستگی مناسبی است.
برای محاسبه همبستگی رتبه اسپیرمن از فرمول زیر استفاده می شود:
ρ= همبستگی رتبه اسپیرمن
di= تفاوت بین رتبه های متغیرهای متناظر
n = تعداد مشاهدات
1-5- انواع مسائل تحقیقی که یک همبستگی اسپیرمن می تواند بررسی کند
آیا بین سطح تحصیلات شرکت کنندگان (دبیرستان، لیسانس یا فوق لیسانس) و حقوق اولیه آنها رابطه معناداری وجود دارد؟
آیا بین موقعیت پایانی اسب در مسابقه و سن اسب رابطه آماری معناداری وجود دارد؟
2-5- مفروضات
مفروضات همبستگی اسپیرمن این است که داده ها باید حداقل ترتیبی باشند و نمرات یک متغیر باید به طور یکنواخت با متغیر دیگر مرتبط باشد.
3-5- کلمات کلیدی
اندازه اثر: مجددا استاندارد کوهن میتواند برای ارزیابی ضریب همبستگی برای تعیین قدرت رابطه یا اندازه اثر استفاده شود. ضرایب همبستگی بین 0.10 و 0.29 نشان دهنده یک ارتباط کوچک، ضرایب بین 0.30 و 0.49 نشان دهنده یک ارتباط متوسط، و ضرایب 0.50 و بالاتر نشان دهنده یک ارتباط یا رابطه بزرگ است.
داده های ترتیبی: در مقیاس ترتیبی، سطوح یک متغیر به گونه ای مرتب می شوند که می توان یک سطح را بالاتر/پایین تر از سطح دیگر در نظر گرفت. با این حال، مقدار تفاوت بین سطوح لزوما مشخص نیست. یک مثال می تواند رتبه بندی سطوح تحصیلی باشد. مدرک تحصیلات تکمیلی بالاتر از مدرک لیسانس و مدرک لیسانس بالاتر از دیپلم دبیرستان است. با این حال، نمیتوانیم تعیین کنیم که مدرک تحصیلات تکمیلی در مقایسه با مدرک کارشناسی چقدر بالاتر است. همچنین نمی توانیم بگوییم که تفاوت تحصیلات بین مدرک تحصیلات تکمیلی و لیسانس با تفاوت بین مدرک لیسانس و دیپلم یکسان است.
6- ضریب همبستگی Polychoric
همبستگی پلی کوریک یا همبستگی تتراکوریک را می توان به عنوان نوع ضریبی بیان کرد که قرار است برای استخراج تفسیر ارتباط دو مشاهدات پیوسته توزیع شده گاوسی که از طریق نظرسنجی ها و آزمون های شخصیتی که برای تولید مقیاس های رتبه بندی مورد نیاز است، جمع آوری شوند. فرمول این ضریب را می توان از ضریب همبستگی پیرسون در صورت داشتن داده های پیوسته به دست آورد.
نتیجه گیری
هنگامی که با مشکلی مواجه می شویم که نیاز به درک قدرت همبستگی در مجموعه داده دارد، مهم است که بتوانیم نوع صحیح ضریب همبستگی را برای اعمال تشخیص دهیم. برای اینکه بتوانیم دقیقاً نوع همبستگی را تعیین کنیم، اول از همه، تجسم داده ها برای درک اینکه آیا توزیع گاوسی دارد یا خیر، ممکن است مفید باشد. در صورت وجود آن، ممکن است به بررسی عمیقتر جنبههای دیگر آن به عنوان انواع و تعداد متغیرها هدایت شویم.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]