آنالیز واریانس (ANOVA) چیست؟ انواع، کاربرد و فرمول

چکیده مقاله:
ANOVA، که مخفف آنالیز واریانس است، یک روش آماری است که برای بررسی تفاوت های معنادار بین میانگین های سه یا چند گروه غیرمرتبط استفاده می شود. این تکنیک به ویژه زمانی مفید است که بخواهید بیش از دو گروه را مقایسه کنید، که یکی از محدودیت های آزمون های دیگر مانند آزمون t و آزمون z است. به عنوان مثال، ANOVA می تواند میانگین نمرات IQ را در چندین کشور مانند ایالات متحده، کانادا، ایتالیا و اسپانیا مقایسه کند تا ببیند آیا ملیت بر نمرات IQ تأثیر می گذارد یا خیر. رونالد فیشر آنالیز واریانس را در سال 1918 توسعه داد و با این کار قابلیت های آزمون های قبلی را گسترش داد، زیرا امکان مقایسه چندین گروه به صورت همزمان را فراهم کرد. این روش همچنین با عنوان تحلیل واریانس فیشر شناخته می شود که توانایی آن در تحلیل تأثیر یک متغیر دسته بندی شده با سطوح متعدد بر یک متغیر پیوسته را برجسته می کند.
آنالیز واریانس چیست؟
آنالیز واریانس (ANOVA) یک آزمون آماری است که برای ارزیابی تفاوت بین میانگین های بیش از دو گروه به کار می رود.
آزمون واریانس (ANOVA) به شما امکان می دهد که به طور همزمان میانگین های چند گروه را مقایسه کنید. این آزمون مشخص می کند که آیا تفاوت های مشاهده شده ناشی از شانس هستند یا نشان دهنده تفاوت های واقعی و معنادار می باشند.
یک آنالیز واریانس یک طرفه از یک متغیر مستقل استفاده می کند، در حالی که ANOVA دو طرفه از دو متغیر مستقل بهره می گیرد. تحلیل گران از این آزمون برای بررسی تأثیر متغیرهای مستقل بر متغیر وابسته در یک مطالعه رگرسیون استفاده می کنند. اگرچه این روش ممکن است برای تازه واردان به آمار پیچیده به نظر برسد، اما کاربردهای آنالیز واریانس بسیار متنوع و عمیق هستند. از محققان پزشکی که به دنبال بررسی اثربخشی درمان های جدید هستند تا بازاریابانی که ترجیحات مصرف کنندگان را تحلیل می کنند، ANOVA به ابزاری ضروری برای درک سیستم های پیچیده و تصمیم گیری مبتنی بر داده تبدیل شده است.
نکات کلیدی:
- ANOVA یک روش آماری است که به طور همزمان میانگین های چند گروه را مقایسه می کند تا مشخص کند که آیا تفاوت های مشاهده شده ناشی از شانس هستند یا تفاوت های واقعی و معناداری را نشان می دهند.
- ANOVA یکطرفه یک متغیر مستقل دارد، در حالی که ANOVA دوطرفه دو متغیر مستقل دارد.
- با تقسیم واریانس کل به اجزای مختلف، ANOVA روابط بین متغیرها را شناسایی کرده و منابع واقعی تغییرات را شفاف می کند.
- ANOVA می تواند عوامل و تعاملات مختلف را مدیریت کند و روشی قدرتمند برای درک روابط پیچیده ارائه می دهد.
کاربرد آنالیز واریانس
آزمون ANOVA زمانی به کار می رود که داده ها نیاز به آزمایش داشته باشند. وقتی دسترسی به نرم افزارهای آماری وجود نداشته باشد، می توان ANOVA را به صورت دستی محاسبه کرد. این روش ساده بوده و برای نمونه های کوچک که شامل آزمودنی ها، گروه های آزمایشی و مقایسه بین و درون گروه ها است، مناسب می باشد.
آنالیز واریانس مشابه چندین آزمون t-دو نمونه ای است، اما تعداد خطاهای نوع اول (Type I) کمتری ایجاد می کند. این آزمون تفاوت های گروه ها را با مقایسه میانگین های هر گروه و تقسیم واریانس به منابع مختلف بررسی می کند. در ANOVA یک طرفه از داده های جمع آوری شده درباره یک متغیر مستقل و یک متغیر وابسته استفاده می شود، در حالی که ANOVA دو طرفه از دو متغیر مستقل بهره می گیرد. متغیر مستقل باید حداقل سه گروه یا دسته مختلف داشته باشد. آنالیز واریانس تعیین می کند که آیا متغیر وابسته بسته به سطح متغیر مستقل تغییر می کند یا خیر.
برای مثال، محققان ممکن است دانشجویان چندین دانشگاه را بررسی کنند تا مشخص کنند آیا دانشجویان یکی از این دانشگاه ها به طور مداوم عملکرد بهتری نسبت به دیگران دارند یا نه. در یک کاربرد تجاری، یک پژوهشگر توسعه و تحقیق ممکن است دو روش تولید یک محصول را بررسی کند تا مشخص کند کدام یک از نظر هزینه کارآمدتر است.
انعطاف پذیری و قابلیت ANOVA در مدیریت متغیرهای متعدد، آن را به ابزاری ارزشمند برای محققان و تحلیل گران در حوزه های مختلف تبدیل کرده است. با مقایسه میانگین ها و تقسیم واریانس، ANOVA روشی قدرتمند برای درک روابط بین متغیرها و شناسایی تفاوت های معنادار بین گروه ها ارائه می دهد.
انواع آنالیز واریانس
استفاده از تحلیل واریانس به طرح تحقیق بستگی دارد. معمولاً ANOVA به سه روش استفاده می شود: تحلیل واریانس یک طرفه، تحلیل واریانس دو طرفه و تحلیل واریانس N طرفه.
ANOVA یک طرفه (One-Way ANOVA)
ANOVA یک طرفه یک روش آماری است که زمانی استفاده می شود که بخواهیم تأثیر یک عامل خاص را بر یک نتیجه مشخص بررسی کنیم. برای مثال، اگر بخواهیم بررسی کنیم که چگونه نمرات IQ بر اساس کشور متفاوت هستند، از ANOVA یک طرفه استفاده می کنیم.
عبارت “یک طرفه” به این معنا است که تنها یک متغیر مستقل را در نظر می گیریم، که در این مثال همان کشور است. با این حال، این متغیر کشور می تواند شامل هر تعداد دسته باشد؛ از دو کشور گرفته تا بیست یا بیشتر.
ANOVA دو طرفه (Two-Way ANOVA)
در یک گام فراتر، ANOVA دو طرفه که به آن ANOVA فاکتوریال نیز گفته می شود، به ما امکان می دهد تأثیر دو عامل مختلف را به طور همزمان بر یک نتیجه بررسی کنیم.
با ادامه مثال قبلی، می توانیم بررسی کنیم که چگونه هر دو عامل کشور و جنسیت بر نمرات IQ تأثیر می گذارند. این روش نه تنها تأثیرات جداگانه هر عامل را مشخص می کند، بلکه امکان بررسی تأثیر متقابل (Interaction Effect) بین آن ها را نیز فراهم می کند.
تأثیر متقابل به این معنا است که تأثیر یک عامل ممکن است بسته به سطح عامل دیگر تغییر کند. برای مثال، ممکن است تفاوت نمرات IQ بین جنسیت ها در کشورهای مختلف متفاوت باشد. این نشان می دهد که تأثیر جنسیت بر IQ در همه کشورها یکسان نیست.
ANOVA چند طرفه (N-Way ANOVA)
زمانی که محققان بیش از دو عامل برای بررسی داشته باشند، از ANOVA چند طرفه استفاده می کنند، که در آن “n” نمایانگر تعداد متغیرهای مستقل در تحلیل است.
برای مثال، می توان بررسی کرد که چگونه ترکیبی از عوامل مانند کشور، جنسیت، گروه سنی و نژاد به طور همزمان بر نمرات IQ تأثیر می گذارند. ANOVA چند طرفه امکان تحلیل جامع تأثیرات متقابل این عوامل مختلف و تأثیر ترکیبی آن ها بر متغیر وابسته را فراهم می کند و درک عمیق تری از دینامیک های موجود ارائه می دهد.
فرمول آنالیز واریانس
که در آن:
- F: ضریب ANOVA
- MST: میانگین مجموع مربعات ناشی از درمان
- MSE: میانگین مجموع مربعات ناشی از خطا
تاریخچه آنالیز واریانس
روش های آزمون t و z که در قرن بیستم توسعه یافتند، برای تحلیل های آماری به کار می رفتند. در سال 1918، زمانی که رونالد فیشر روش تحلیل واریانس را ایجاد کرد، ANOVA متولد شد.
به همین دلیل، آنالیز واریانس همچنین به عنوان تحلیل واریانس فیشر نیز شناخته می شود و توسعه ای از آزمون های t و z است. این اصطلاح در سال 1925، پس از انتشار در کتاب فیشر با عنوان “روش های آماری برای پژوهشگران” شهرت یافت. ابتدا این روش در روانشناسی تجربی به کار گرفته شد و سپس به سایر حوزه ها گسترش یافت.
آزمون ANOVA اولین گام در تحلیل عوامل مؤثر بر یک مجموعه داده معین است. پس از اتمام آزمون، تحلیل گر آزمون های بیشتری روی عواملی که به طور قابل اندازه گیری ممکن است به ناسازگاری داده ها کمک کنند، انجام می دهد. تحلیل گر از نتایج آزمون ANOVA در یک آزمون F برای تولید داده های بیشتری که با مدل های رگرسیون پیشنهادی همخوانی دارند، استفاده می کند.
راهنمای آزمون های آماری رایج در امور مالی و سرمایه گذاری
| آزمون | هدف | زمان استفاده | کاربرد در امور مالی/سرمایه گذاری |
|---|---|---|---|
| ANCOVA | مقایسه میانگین های دو یا چند گروه با کنترل اثر یک متغیر پیوسته | توزیع نرمال، مقایسه متغیرهای مستقل متعدد با یک متغیر همگرا | تحلیل بازده سرمایه گذاری با کنترل نوسانات بازار، ارزیابی استراتژی های مالی با در نظر گرفتن شرایط اقتصادی |
| ANOVA | مقایسه میانگین های سه یا چند گروه | داده های دارای توزیع نرمال | مقایسه عملکرد مالی در بخش های مختلف یا استراتژی های سرمایه گذاری |
| آزمون Chi-Square | بررسی ارتباط بین دو متغیر دسته بندی شده (غیر عددی) | داده های دسته بندی شده (مثلاً انتخاب سرمایه گذاری، بخش های بازار) | تحلیل جمعیت شناسی مشتریان و تخصیص پرتفوی |
| Correlation | اندازه گیری شدت و جهت رابطه خطی بین دو متغیر | داده های پیوسته | ارزیابی ریسک و بازده دارایی ها، متنوع سازی پرتفوی |
| آزمون Durbin-Watson | بررسی ارتباط خطاها در مدل پیش بینی در طول زمان | داده های سری زمانی | شناسایی همبستگی سریالی در قیمت سهام و روندهای بازار |
| آزمون F | مقایسه واریانس های دو یا چند گروه | داده های دارای توزیع نرمال | بررسی برابری واریانس بازده سهام و عملکرد پرتفوی |
| آزمون Granger Causality | بررسی رابطه علّی بین دو سری زمانی | داده های سری زمانی | تعیین اینکه آیا یک شاخص اقتصادی می تواند دیگری را پیش بینی کند |
| آزمون Jarque-Bera | بررسی نرمال بودن داده ها | داده های پیوسته | ارزیابی اینکه آیا داده های مالی دارای توزیع نرمال هستند |
| آزمون Mann-Whitney U | مقایسه میانه های دو نمونه مستقل | داده های غیر نرمال | مقایسه عملکرد مالی دو گروه با توزیع غیر نرمال |
| MANOVA | مقایسه میانگین های دو یا چند گروه برای چندین متغیر وابسته به صورت همزمان | داده های دارای توزیع نرمال، تحلیل متغیرهای خروجی مرتبط | ارزیابی تأثیر پرتفوی های مختلف بر چندین معیار مالی، بررسی سلامت کلی شرکت ها بر اساس شاخص های مختلف عملکرد |
| آزمون T یک نمونه ای | مقایسه میانگین نمونه با میانگین شناخته شده جمعیت | داده های دارای توزیع نرمال یا حجم نمونه بزرگ | مقایسه بازده واقعی در مقابل بازده مورد انتظار |
| آزمون T زوجی | مقایسه میانگین های دو نمونه مرتبط (مانند اندازه گیری های قبل و بعد) | داده های دارای توزیع نرمال یا حجم نمونه بزرگ | بررسی اثربخشی یک تغییر مالی |
| رگرسیون | پیش بینی مقدار یک متغیر بر اساس مقدار متغیر دیگر | داده های پیوسته | مدل سازی قیمت سهام، پیش بینی بازده های آینده |
| آزمون Sign | بررسی تفاوت در میانه های دو نمونه مرتبط | داده های غیر نرمال | جایگزین غیر پارامتری برای آزمون t زوجی در مطالعات مالی |
| آزمون T | مقایسه میانگین های دو گروه | داده های دارای توزیع نرمال یا حجم نمونه بزرگ | مقایسه عملکرد دو استراتژی سرمایه گذاری |
| آزمون Wilcoxon Rank-Sum | مقایسه میانه های دو نمونه مستقل | داده های غیر نرمال | جایگزین غیر پارامتری برای آزمون t مستقل در امور مالی |
| آزمون Z | مقایسه میانگین نمونه با میانگین شناخته شده جمعیت | داده های دارای توزیع نرمال و انحراف استاندارد جمعیت مشخص | بررسی فرضیه درباره میانگین های بازار |
آنچه ANOVA آشکار می کند
آنالیز واریانس تغییرپذیری مشاهده شده در یک مجموعه داده را به دو بخش تقسیم می کند: عوامل سیستماتیک و عوامل تصادفی. عوامل سیستماتیک بر مجموعه داده تأثیر می گذارند، در حالی که عوامل تصادفی چنین اثری ندارند.
آزمون ANOVA به شما امکان می دهد که به طور همزمان بیش از دو گروه را مقایسه کنید تا تعیین کنید آیا رابطه ای بین آن ها وجود دارد یا خیر. نتیجه فرمول آنالیز واریانس، یعنی آماره F یا نسبت F، به شما امکان می دهد گروه های مختلف داده را تحلیل کرده و تغییرپذیری بین نمونه ها و درون نمونه ها را ارزیابی کنید.
اگر هیچ تفاوت واقعی بین گروه های مورد آزمایش وجود نداشته باشد (فرضیه صفر)، نتیجه آماره نسبت F در آنالیز واریانس به عدد یک نزدیک خواهد بود. توزیع تمامی مقادیر ممکن آماره F، توزیع F نام دارد. این توزیع شامل گروهی از توابع توزیع با دو عدد مشخصه است که به آن ها درجات آزادی صورت (numerator degrees of freedom) و درجات آزادی مخرج (denominator degrees of freedom) گفته می شود.
تفاوت آنالیز واریانس یک طرفه و دو طرفه
| ویژگیها | آنالیز واریانس یک طرفه | آنالیز واریانس دو طرفه |
|---|---|---|
| تعداد متغیرهای مستقل | از یک متغیر مستقل یا عامل استفاده می کند | از دو متغیر مستقل یا عامل استفاده می کند |
| هدف | بررسی تأثیر یک متغیر دسته بندی شده بر یک متغیر وابسته پیوسته و شناسایی تفاوت های معنادار میان میانگین گروه ها | بررسی تأثیرات جداگانه دو عامل متفاوت و همچنین نحوه ترکیب این دو عامل بر نتیجه |
| تعامل بین عوامل | تعاملات را در نظر نمی گیرد | می تواند تعامل بین عوامل را آزمون کند |
ANOVA یکطرفه
ANOVA یکطرفه تأثیر یک عامل را بر یک متغیر پاسخ مشخص بررسی می کند. این آزمون تعیین می کند که آیا تمامی نمونه ها یکسان هستند یا خیر. ANOVA یکطرفه برای شناسایی تفاوت های معنادار آماری بین میانگین های سه یا چند گروه مستقل به کار می رود.
ANOVA دوطرفه
ANOVA دوطرفه گسترشی از ANOVA یکطرفه است. در ANOVA یکطرفه یک متغیر مستقل بر یک متغیر وابسته تأثیر می گذارد. اما در ANOVA دوطرفه دو متغیر مستقل وجود دارند. برای مثال، ANOVA دوطرفه به یک شرکت امکان می دهد که بهره وری کارکنان را بر اساس دو متغیر مستقل، مانند حقوق و مجموعه مهارت ها، مقایسه کند. این روش برای مشاهده تعامل بین دو عامل و آزمون تأثیر دو عامل به طور همزمان استفاده می شود.
مثال ANOVA
فرض کنید قصد دارید عملکرد پرتفوی های سرمایه گذاری مختلف را در شرایط مختلف بازار ارزیابی کنید. هدف این است که مشخص شود کدام استراتژی پرتفوی در چه شرایطی بهترین عملکرد را دارد.
شما سه استراتژی پرتفوی دارید:
- پرتفوی فناوری (سهام فناوری): پرریسک با بازدهی بالا
- پرتفوی متعادل (سهام و اوراق قرضه): ریسک متوسط با بازدهی متوسط
- پرتفوی درآمد ثابت (اوراق قرضه و ابزارهای بازار پول): کمریسک با بازدهی پایین
همچنین می خواهید عملکرد را در دو شرایط بازار بررسی کنید:
- بازار گاوی
- بازار خرسی
یک ANOVA یکطرفه می تواند نمای کلی از عملکرد استراتژی های پرتفوی ارائه دهد، در حالی که ANOVA دوطرفه تحلیل عمیق تری ارائه می دهد و شرایط مختلف بازار را نیز شامل می شود.
ANOVA یک طرفه
ANOVA یکطرفه می تواند برای تحلیل اولیه تفاوت های عملکردی میان سه پرتفوی مختلف بدون در نظر گرفتن تأثیر شرایط بازار استفاده شود. متغیر مستقل نوع پرتفوی سرمایه گذاری و متغیر وابسته بازدهی تولید شده خواهد بود.
برای این کار، بازدهی پرتفوی فناوری، متعادل و درآمد ثابت را در یک دوره مشخص جمع آوری کرده و میانگین بازدهی سه پرتفوی را مقایسه می کنید تا مشخص شود آیا تفاوت های آماری معناداری وجود دارد یا خیر. این روش تعیین می کند که آیا استراتژی های مختلف سرمایه گذاری منجر به بازدهی متفاوت می شوند یا خیر، اما تأثیر شرایط بازار بر این بازدهی را لحاظ نمی کند.
ANOVA دو طرفه
از طرف دیگر، ANOVA دوطرفه برای تحلیل تأثیرات هر دو عامل استراتژی سرمایه گذاری و شرایط بازار، و همچنین تعامل بین این دو عامل بر بازدهی مناسب تر است.
MANOVA (تحلیل واریانس چندمتغیره) از ANOVA متفاوت است زیرا به طور همزمان چندین متغیر وابسته را آزمون می کند، در حالی که ANOVA تنها یک متغیر وابسته را در هر زمان ارزیابی می کند.
در اینجا ابتدا باید بازدهی هر پرتفوی را در شرایط بازار گاوی و خرسی گروه بندی کنید. سپس میانگین بازدهی را در هر دو عامل مقایسه می کنید تا تأثیر استراتژی سرمایه گذاری بر بازدهی، تأثیر شرایط بازار بر بازدهی و همچنین وابستگی اثربخشی یک استراتژی سرمایه گذاری خاص به شرایط بازار را ارزیابی کنید.
فرض کنید پرتفوی فناوری در بازارهای گاوی عملکرد بسیار بهتری دارد اما در بازارهای خرسی ضعیف عمل می کند، در حالی که پرتفوی درآمد ثابت بازدهی ثابتی را صرف نظر از شرایط بازار ارائه می دهد. مشاهده این تعاملات می تواند به شما کمک کند بفهمید چه زمانی توصیه استفاده از پرتفوی فناوری مناسب است و چه زمانی بازار خرسی به استفاده از پرتفوی درآمد ثابت منطقی تر است.
سوالات متداول
تفاوت ANOVA با آزمون t چیست؟
ANOVA با آزمون t متفاوت است زیرا ANOVA می تواند سه یا چند گروه را مقایسه کند، در حالی که آزمون t فقط برای مقایسه دو گروه در هر زمان مفید است.
تحلیل کوواریانس (ANCOVA) چیست؟
تحلیل کوواریانس ترکیبی از آزمون واریانس و رگرسیون است. این روش برای درک واریانس درونگروهی که آزمون ANOVA توضیح نمی دهد، مفید است.
آیا آنالیز واریانس به فرضیاتی متکی است؟
بله، آزمون های ANOVA فرض می کنند که داده ها به طور نرمال توزیع شده اند و سطح واریانس در هر گروه تقریباً برابر است. در نهایت، فرض می شود که تمامی مشاهدات به طور مستقل انجام شده اند. اگر این فرضیات نادرست باشند، ANOVA ممکن است برای مقایسه گروه ها مفید نباشد.
نتیجه گیری
ANOVA یک ابزار آماری قوی است که به پژوهشگران و تحلیل گران امکان می دهد میانگین های حسابی را به طور همزمان در گروه های مختلف مقایسه کنند. با تقسیم واریانس به منابع مختلف، ANOVA به شناسایی تفاوت های معنادار و کشف روابط مفید بین متغیرها کمک می کند.
تنوع و توانایی ANOVA در پردازش عوامل مختلف آن را به ابزاری ضروری در بسیاری از حوزه هایی که از آمار استفاده می کنند، از جمله امور مالی و سرمایه گذاری، تبدیل کرده است.
درک اصول، انواع و کاربردهای ANOVA برای استفاده مؤثر از این تکنیک بسیار مهم است. چه از ANOVA یکطرفه استفاده شود و چه دوطرفه، پژوهشگران می توانند درک عمیق تری از سیستم های پیچیده به دست آورند تا تصمیمات مبتنی بر داده بگیرند. همانند هر روش آماری، تفسیر نتایج باید با دقت و در نظر گرفتن زمینه و محدودیت های تحلیل انجام شود.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]

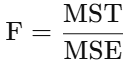











سلام و درود
برای انالیز پایان نامه دکتری در علوم دامی معمولا از نرم افزار sas استفاده میشه. برای انالیز طرح خودم نمیدونم از چه رویه ای که خطا نداشته باشه استفاده کنم.استاد راهنما گفته که از رویه GLM استفاده نکن چون خط داره.
چطور باید متوجه بشم
سلام وقت بخیر
لطفا پروپزال خود را جهت بررسی بیشتر واسمون بفرستین تا بتوانیم دقیق پاسخ دهیم، باتشکر