الگوریتم جستجوی دودویی Binary Search در پایتون

چکیده مقاله :
الگوریتم جستجوی دودویی Binary Search در پایتون یکی از روش های سریع و بهینه برای پیدا کردن یک عنصر در فهرست های مرتب شده می باشد. این الگوریتم بر اساس ایده تقسیم و بررسی عمل می کند؛ به این شکل که در هر مرحله، فهرست به دو بخش تقسیم شده و با مقایسه عنصر میانی با مقدار مورد نظر، نیمی از داده ها کنار گذاشته می شود. با این کار به جای بررسی تک تک عناصر، در هر گام بخش بزرگی از داده حذف می شود و سرعت جستجو به شکل قابل توجهی افزایش پیدا می کند.

در پیاده سازی این الگوریتم به زبان پایتون، ابتدا باید فهرست از قبل به صورت صعودی مرتب شده باشد. سپس با مشخص کردن یک اندیس برای ابتدای فهرست و یک اندیس برای انتها، مقدار میانی محاسبه و با عدد هدف مقایسه می شود. اگر عنصر میانی همان عدد هدف باشد جستجو پایان می یابد. اگر عنصر میانی کوچکتر از عدد هدف باشد، جستجو در نیمه سمت راست فهرست ادامه پیدا می کند و در غیر این صورت جستجو به نیمه سمت چپ محدود می شود. این مراحل تا زمانی ادامه می یابد که مقدار مورد نظر پیدا شود یا محدوده جستجو خالی شود.

الگوریتم جستجوی دودویی Binary Search در پایتون یکی از سریع ترین و بهینه ترین روش ها برای پیدا کردن عناصر در آرایه های مرتب می باشد و کاربردهای گسترده ای در برنامه نویسی و علوم داده دارد.تصور کنید در حال انجام یک بازی حدس عدد هستید که باید یک عدد خاص را بین 1 تا 100 پیدا کنید. اگر بخواهید به صورت تصادفی عدد ها را حدس بزنید، در بدترین حالت ممکن است مجبور شوید همه 100 عدد را امتحان کنید تا به پاسخ درست برسید.

روش کوتاه تر و هوشمندانه تر این است که ابتدا عدد میانی یعنی 50 را انتخاب کنید و بپرسید که آیا عدد هدف شما بزرگ تر است یا کوچک تر. اگر عدد هدف بزرگ تر باشد، کل اعداد کمتر از 50 را نادیده می گیرید و همین فرآیند را برای بازه 51 تا 100 تکرار می کنید. این کار را ادامه می دهید تا زمانی که به عدد درست برسید.

با نصف کردن بازه ها در هر مرحله، خیلی سریع به عدد هدف نزدیک می شوید. در این روش حتی در بدترین حالت هم فقط به 7 حدس نیاز دارید تا پاسخ صحیح را پیدا کنید. این همان استراتژی اصلی الگوریتم جستجوی دودویی Binary Search در پایتون است.

در این راهنما، به طور کامل بررسی می کنیم که جستجوی دودویی چیست، چه کاربرد های عملی دارد و چگونه می توان آن را در پایتون پیاده سازی کرد. در این مسیر هم روش بازگشتی (Recursive) و هم روش تکراری (Iterative) را بررسی می کنیم تا دید جامعی از این الگوریتم به دست آورید.

جستجوی دودویی چیست؟

زمانی که شما به دنبال یک مقدار خاص در یک مجموعه داده هستید، هدف این است که اندیس یا موقعیت آن مقدار را پیدا کنید تا بتوانید به راحتی در کد خود از آن استفاده کنید. الگوریتم های متعددی وجود دارند که می توانند به شما در یافتن اندیس یک مقدار خاص کمک کنند. یکی از موثرترین و بنیادی ترین روش ها برای انجام این کار، الگوریتم جستجوی دودویی Binary Search در پایتون است.

مفهوم جستجوی دودویی

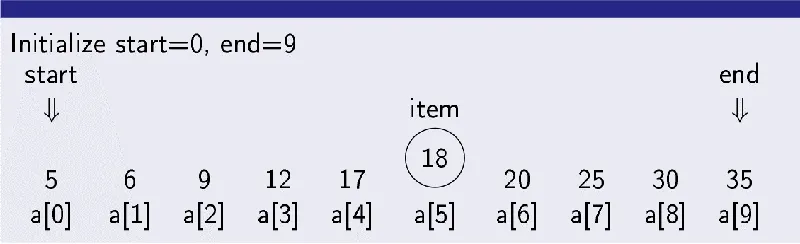
به طور کلی، یک الگوریتم به معنای دنباله ای دقیق از دستورالعمل ها است که یک کامپیوتر برای انجام یک وظیفه خاص یا حل یک مسئله از آن پیروی می کند. الگوریتم جستجوی دودویی یک روش قدرتمند و کاربردی است که برای یافتن سریع یک مقدار در مجموعه داده مرتب شده طراحی شده است. ایده اصلی پشت این الگوریتم ساده و در عین حال بسیار کارآمد است: به جای بررسی تک تک عناصر مجموعه داده، مانند آنچه در جستجوی خطی انجام می شود، جستجوی دودویی در هر مرحله محدوده جستجو را به نصف کاهش می دهد و به همین دلیل سرعت بسیار بیشتری دارد.

مکانیزم عملکرد این الگوریتم به این صورت است:

1. ابتدا مقدار هدف را با عنصر میانی مجموعه داده مقایسه می کنیم. اندیس عنصر میانی با استفاده از فرمول زیر محاسبه می شود:

middle = (low + high) / 2

در این فرمول، مقدار low اندیس اولین عنصر بازه جستجوی فعلی و مقدار high اندیس آخرین عنصر در همان بازه است.

2. سپس عنصر میانی با مقدار هدف مقایسه می شود. اگر مقدار هدف دقیقا برابر با عنصر میانی باشد، اندیس آن پیدا شده و جستجو به پایان می رسد. اگر مقدار هدف کوچکتر از عنصر میانی باشد، ادامه جستجو در نیمه چپ مجموعه داده انجام می شود. اما اگر مقدار هدف بزرگ تر باشد، جستجو در نیمه راست ادامه پیدا می کند.
3. این فرآیند یعنی گام های 1 و 2 به طور مداوم تکرار می شوند. در هر مرحله محدوده جستجو نصف می شود و این کار ادامه پیدا می کند تا یا مقدار هدف پیدا شود و یا محدوده جستجو خالی گردد.

این روش به دلیل کارایی بالا و کاهش چشمگیر تعداد مقایسه ها، به یکی از الگوریتم های پایه ای و بسیار پرکاربرد در علوم کامپیوتر تبدیل شده است. به همین دلیل بسیاری از توسعه دهندگان هنگام کار با داده های بزرگ و مرتب شده، از الگوریتم جستجوی دودویی Binary Search در پایتون به عنوان راهکاری سریع و مطمئن استفاده می کنند.

این فرآیند نصف کردن بازه ها همان چیزی است که الگوریتم جستجوی دودویی را بسیار کارآمد می کند. با این حال باید توجه داشت که مجموعه داده حتما باید مرتب شده باشد تا این الگوریتم به درستی کار کند. اگر داده ها مرتب نشده باشند، این روش عملکرد صحیحی نخواهد داشت و نمی تواند مقدار هدف را پیدا کند.

نکات کلیدی برای به خاطر سپردن

موارد زیر اصول اصلی الگوریتم جستجوی دودویی Binary Search در پایتون را نشان می دهند:

• کارایی

جستجوی دودویی به شکل قابل توجهی سریع تر از جستجوی خطی عمل می کند، به ویژه زمانی که با مجموعه داده های بزرگ سر و کار داریم. در حالی که جستجوی خطی دارای پیچیدگی زمانی O(n) است، به این معنا که در بدترین حالت باید تک تک عناصر بررسی شوند، جستجوی دودویی بسیار کارآمد تر است. این الگوریتم پیچیدگی زمانی O(log n) دارد؛ یعنی در هر مرحله فضای جستجو نصف می شود و به همین دلیل تعداد مقایسه ها به شدت کاهش می یابد.

• پیش نیازها

برای این که جستجوی دودویی درست کار کند، مجموعه داده باید به صورت صعودی یا نزولی مرتب شده باشد. این یک الزام اساسی است زیرا الگوریتم برای انتخاب نیمه بعدی جهت جستجو به ترتیب عناصر تکیه دارد. اگر داده ها مرتب نباشند، جستجوی دودویی نمی تواند مقدار هدف را به درستی پیدا کند.

• انعطاف پذیری

الگوریتم جستجوی دودویی Binary Search در پایتون را می توان هم به روش تکراری (Iterative) و هم به روش بازگشتی (Recursive) پیاده سازی کرد. در روش تکراری از حلقه ها برای نصف کردن مداوم بازه جستجو استفاده می شود، در حالی که در روش بازگشتی تابع خودش را با بازه کوچکتر فراخوانی می کند. این انعطاف پذیری باعث می شود بتوان از آن در کاربردهای متنوع بهره گرفت.

پیاده سازی الگوریتم جستجوی دودویی Binary Search در پایتون

حالا وقتشه ببینیم این الگوریتم قدرتمند رو چطور می‌شه در عمل پیاده‌سازی کرد. برای شروع، یک آرایه‌ی مرتب ساده داریم و می‌خواهیم یک مقدار مشخص رو داخل اون پیدا کنیم:

1. روش تکراری (Iterative Method)

روش تکراری یکی از ساده‌ ترین و پرکاربرد ترین پیاده‌سازی ‌هاست. در این روش با استفاده از یک حلقه‌ی while بازه‌ی جستجو رو مرتب نصف می‌کنیم تا به مقدار هدف برسیم. این روش هم واضح و هم کارآمده.

def binary_search_iterative(arr, target):

# اجرای کد

بیایید نگاهی دقیق تر به این کد بیندازیم:

در ابتدا ما دو متغیر به نام های  left و right را به عنوان مرز های محدوده جستجو مشخص می کنیم. مقدار اولیه  left برابر 0 است (شروع آرایه) و مقدار اولیه  right برابر است با len(arr) – 1 یعنی اندیس آخرین عنصر آرایه.

در هر مرحله از اجرای حلقه، اندیس میانی یا همان  mid محاسبه می شود که نشان دهنده عنصر وسط در بازه فعلی جستجو است. فرمول محاسبه آن به شکل زیر است:

mid = left + (right – left) // 2

سپس مقدار عنصر موجود در اندیس  mid با مقدار هدف یا همان  target مقایسه می شود:

• اگر مقدار وسط دقیقا با مقدار هدف برابر باشد، یعنی عنصر مورد نظر پیدا شده و تابع اندیس آن را برمی گرداند.
• اگر مقدار عنصر وسط کمتر از مقدار هدف باشد، یعنی عنصر هدف باید در نیمه راست آرایه قرار داشته باشد. بنابراین مقدار left برابر با mid + 1 می شود.
• اگر مقدار عنصر وسط بزرگتر از مقدار هدف باشد، یعنی عنصر مورد نظر در نیمه چپ قرار دارد. در این حالت مقدار right برابر با  mid – 1 خواهد شد.

این روند تا زمانی ادامه پیدا می کند که یا عنصر هدف پیدا شود یا اینکه مقدار left از right بزرگتر شود که به معنای نبودن مقدار هدف در آرایه است.

2. روش بازگشتی

علاوه بر روش تکراری یا همان استفاده از حلقه، الگوریتم جستجوی دودویی را می توان با روش بازگشتی هم پیاده سازی کرد. در این روش به جای تکرار با حلقه، تابع به صورت خودکار خودش را فراخوانی می کند و در هر بار فراخوانی، محدوده جستجو کوچکتر و دقیق تر می شود تا در نهایت یا مقدار هدف پیدا شود یا به این نتیجه برسیم که مقدار مورد نظر در آرایه وجود ندارد.

کد زیر نمونه ای از پیاده سازی روش بازگشتی الگوریتم Binary Search در پایتون است:

بیایید نگاهی دقیق تر به این کد بیندازیم:

تابع بازگشتی الگوریتم جستجوی دودویی در پایتون دقیقا با همان مرزهای اولیه left و right شروع می شود که در نسخه تکراری هم داشتیم. به عبارت دیگر نقطه شروع در هر دو روش یکسان است.

در اولین قدم، بررسی می شود که آیا مقدار left از right بزرگتر شده است یا نه. اگر چنین حالتی رخ دهد یعنی محدوده جستجو خالی شده و عنصر هدف در آرایه وجود ندارد، پس مقدار -1 بازگردانده می شود.

اگر محدوده معتبر باشد، اندیس وسط یا همان mid محاسبه می شود و سپس مقدار موجود در این اندیس با مقدار هدف یا target مقایسه می گردد.

• اگر مقدار عنصر وسط دقیقا برابر با مقدار هدف باشد، تابع اندیس آن عنصر را بازمی گرداند.
• اگر مقدار هدف بزرگتر از عنصر وسط باشد، یعنی باید در نیمه سمت راست آرایه جستجو کنیم. در این حالت تابع خودش را دوباره صدا می زند اما با مقادیر جدید برای left و right که محدوده جستجو را به سمت راست محدود می کنند.
• اگر مقدار هدف کوچکتر از عنصر وسط باشد، جستجو به صورت بازگشتی در نیمه سمت چپ ادامه پیدا می کند.

این فرآیند بازگشتی تا زمانی تکرار می شود که یا عنصر مورد نظر پیدا شود یا محدوده جستجو کاملا خالی گردد. در نتیجه روش بازگشتی الگوریتم Binary Search Python همانند روش تکراری، تضمین می کند که در کوتاه ترین زمان ممکن به نتیجه برسیم.

برای آشنایی بیشتر با توابع بازگشتی می توانید مقاله «درک توابع بازگشتی در پایتون» را مطالعه کنید که به صورت کامل این موضوع را توضیح می دهد و ارتباط آن با الگوریتم هایی مثل الگوریتم جستجوی دودویی در پایتون را نشان می دهد.

3. استفاده از ماژول داخلی bisect در پایتون

کتابخانه استاندارد پایتون شامل ماژولی به نام  bisect می باشد که توابع از پیش پیاده سازی شده برای انجام جستجوی دودویی را در اختیار ما قرار می دهد. استفاده از این ماژول در بسیاری از مواقع بسیار کارآمدتر از نوشتن دستی توابع جستجو است و به توسعه دهنده کمک می کند تا در وقت و منابع صرفه جویی کند.

مزیت اصلی این ماژول در این است که الگوریتم Binary Search Python را به صورت بهینه پیاده سازی کرده و نیازی نیست از ابتدا کدنویسی کنیم. علاوه بر این، دقت بالایی در پردازش داده های مرتب دارد و به راحتی می توان آن را در پروژه های واقعی مورد استفاده قرار داد.

در ادامه مشاهده می کنید که چگونه می توانیم با کمک ماژول bisect عنصر هدف را در یک آرایه مرتب پیدا کنیم:

تابع bisect_left در ماژول bisect اندیسی را برمی گرداند که اگر عنصر هدف (target) در آن موقعیت قرار گیرد، ترتیب مرتب آرایه حفظ می شود. به عبارت دیگر، اگر مقدار هدف دقیقا در این اندیس یافت شود، یعنی عنصر مورد نظر در آرایه موجود است.

این روش به ویژه زمانی کاربردی است که با آرایه های مرتب کار می کنیم و می خواهیم علاوه بر جستجو، عناصر جدید را نیز بدون به هم خوردن ترتیب آرایه اضافه کنیم. به این ترتیب، عملکرد الگوریتم جستجوی دودویی در پایتون به صورت بسیار بهینه تر و سریع تر انجام می شود.

علاوه بر bisect_left، ماژول bisect توابع دیگری نیز ارائه می دهد، مانند:

• bisect_right که نقطه مناسب برای قرار دادن عنصر هدف در سمت راست عناصر مشابه را مشخص می کند.
• insort که به طور مستقیم عنصر جدید را در موقعیت مناسب وارد آرایه می کند و ترتیب مرتب آرایه را حفظ می کند.

این توابع باعث می شوند که مدیریت و جستجو در آرایه های مرتب بسیار ساده و سریع باشد و می توان از آن ها به عنوان نسخه آماده و بهینه الگوریتم Binary Search Python استفاده کرد.

کاربردهای جستجوی دودویی در دنیای واقعی

الگوریتم جستجوی دودویی ابزاری قدرتمند است. توانایی آن در کوچک کردن سریع بازه جستجو باعث شده به ویژه هنگام کار با مجموعه داده های بزرگ که سرعت و کارایی اهمیت زیادی دارد، بسیار ارزشمند باشد. حالا بیایید به برخی کاربردهای مشخص نگاه کنیم و ببینیم که این الگوریتم در مقایسه با سایر روش ها چه جایگاهی دارد.

1. پایگاه داده ها

در سیستم های پایگاه داده، جستجوی دودویی برای یافتن سریع رکوردها در فیلدهای مرتب شده مورد استفاده قرار می گیرد. به عنوان مثال فرض کنید یک دیتابیس میلیون ها رکورد دارد و ما به دنبال یک کاربر خاص هستیم. در جستجوی خطی باید رکوردها یکی یکی بررسی شوند که زمان زیادی می گیرد. اما الگوریتم جستجوی دودویی Binary Search در پایتون می تواند با نصف کردن فضای جستجو در هر مرحله، خیلی سریع به رکورد مورد نظر برسد و تعداد مقایسه ها را به شدت کاهش دهد.

2. علم داده

جستجو در مجموعه داده های مرتب شده یکی از کارهای رایج در علم داده است. مثلا در تحلیل سری های زمانی، جستجوی دودویی می تواند برای پیدا کردن یک زمان مشخص در بین دنباله ای مرتب از رویدادها به کار رود. در یادگیری ماشین نیز این الگوریتم می تواند برای بهینه سازی هایپرپارامترها استفاده شود تا بهترین مقدار در یک بازه مشخص پیدا شود.

3. گرافیک کامپیوتری

در گرافیک کامپیوتری، الگوریتم جستجوی دودویی در جاهایی که دقت و سرعت اهمیت بالایی دارند مورد استفاده قرار می گیرد. یکی از مثال ها، تکنیک رندرینگ “Ray Tracing” است که برای شبیه سازی نحوه تعامل نور با اشیا به کار می رود. در اینجا جستجوی دودویی می تواند برای یافتن سریع نقاط تقاطع پرتوها و سطوح استفاده شود.

4. پایه ای برای الگوریتم های پیچیده تر

الگوریتم جستجوی دودویی تنها به تنهایی مفید نیست، بلکه پایه و اساس بسیاری از الگوریتم ها و ساختار داده های پیشرفته تر را تشکیل می دهد. مثلا درخت های جستجوی دودویی (BST) یا درخت های متوازن مانند AVL Tree همگی بر مبنای اصول همین الگوریتم ساخته شده اند. این ساختارها امکان جستجو، درج و حذف کارآمد داده ها را فراهم می کنند و به همین دلیل در کاربردهایی که داده ها باید به صورت پویا تغییر و جستجو شوند بسیار پرکاربرد هستند.

مقایسه جستجوی دودویی با سایر الگوریتم ها

بیایید ببینیم الگوریتم جستجوی دودویی Binary Search در پایتون چگونه در برابر دو روش رایج دیگر یعنی جستجوی خطی و هش لوکاپ عمل می کند.

• جستجوی خطی

جستجوی خطی ساده ترین الگوریتم است که عناصر مجموعه داده را به ترتیب و یکی یکی بررسی می کند. این روش به مراتب از جستجوی دودویی کندتر است زیرا پیچیدگی زمانی آن O(n) می باشد. البته مزیت آن این است که نیازی به مرتب بودن داده ها ندارد و در بعضی شرایط کاربردی خواهد بود.

• هش لوکاپ (Hash Lookup)

هش لوکاپ یکی از سریع ترین روش ها برای یافتن مقادیر در مجموعه داده است، به ویژه زمانی که داده ها با کلیدهای یکتا همراه هستند. در این روش یک تابع هش روی کلید اعمال می شود و اندیسی که مقدار در آن ذخیره شده محاسبه می گردد. این فرآیند امکان دسترسی تقریبا فوری به داده ها را فراهم می کند و معمولا زمان اجرای آن O(1) است. با این حال این روش به حافظه بیشتری برای نگهداری جدول هش نیاز دارد و برای جستجو در یک بازه از مقادیر مناسب نیست. در چنین مواردی، الگوریتم جستجوی دودویی گزینه بسیار بهتری محسوب می شود.