آزمون کای دو – توزیع کای 2 یا خی دو چیست؟ (Chi-Square)

چکیده مقاله :
آزمون مجذور کای (همچنین آزمون کای اسکوئر یا χ2) یک آزمون فرضیه آماری است که در تجزیه و تحلیل جداول احتمالی زمانی که حجم نمونه بزرگ است استفاده می شود. به عبارت ساده تر، این آزمون در درجه اول برای بررسی اینکه آیا دو متغیر طبقه بندی شده (دو بعد جدول اقتضایی) در تأثیرگذاری بر آمار آزمون (مقادیر درون جدول) مستقل هستند یا خیر، استفاده می شود. آزمون کای دو پیرسون برای تعیین اینکه آیا تفاوت آماری معنی داری بین فرکانس های مورد انتظار و فرکانس های مشاهده شده در یک یا چند دسته از جدول اقتضایی وجود دارد یا خیر استفاده می شود. برای جداول احتمالی با اندازه نمونه کوچکتر، به جای آن از آزمون دقیق فیشر استفاده می شود. در این محتوا به بررسی کامل آزمون کای 2 می پردازیم. مفهوم کای 2 یا همان خی دو را به همراه مثال و نحوه استفاده توضیح می دهیم.

1- کای 2 در آمار چیست؟

کای 2 (χ2) آزمونی است که نحوه مقایسه یک مدل با داده های مشاهده شده واقعی را اندازه گیری می کند. داده های مورد استفاده در محاسبه کای اسکوئر باید تصادفی، خام، متقابلاً انحصاری، از متغیرهای مستقل و از نمونه به اندازه کافی بزرگ استخراج شده باشد. به عنوان مثال، نتایج پرتاب یک سکه منصفانه با این معیارها مطابقت دارد.

از آزمون های مجذور کای اغلب برای آزمون فرضیه ها استفاده می شود. کای 2 اندازه هر گونه اختلاف بین نتایج مورد انتظار و نتایج واقعی را با توجه به اندازه نمونه و تعداد متغیرهای موجود در رابطه مقایسه می کند.

برای این آزمون ها، درجات آزادی برای تعیین اینکه آیا می توان یک فرضیه صفر معین را بر اساس تعداد کل متغیرها و نمونه های درون آزمایش رد کرد یا خیر، استفاده می شود. مانند هر آماری، هرچه حجم نمونه بزرگتر باشد، نتایج قابل اعتمادتر است.

جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تحلیل آماری چیست مطالعه نمایید.

• تحلیل آماری چیست ؟

مفاهیم کلیدی

• آزمون کای دو (χ2) اندازه گیری تفاوت بین فراوانی های مشاهده شده و مورد انتظار نتایج مجموعه ای از رویدادها یا متغیرها است.
• مجذور کای برای تجزیه و تحلیل چنین تفاوت هایی در متغیرهای طبقه ای، به ویژه آنهایی که ماهیت اسمی دارند، مفید است.
• χ2 به اندازه تفاوت بین مقادیر واقعی و مشاهده شده، درجات آزادی و حجم نمونه بستگی دارد.
• از آزمون کای دو می توان برای آزمایش اینکه آیا دو متغیر مرتبط یا مستقل از یکدیگر هستند استفاده کرد.
• همچنین می توان از آن برای آزمایش خوب بودن تناسب بین توزیع مشاهده شده و توزیع نظری فرکانس ها استفاده کرد.

2- فرمول کای 2

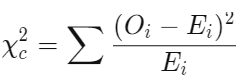
که در آن:
c=درجات آزادی
O=مقدار(های) مشاهده شده
E=مقدار(های) مورد انتظار

3- آزمون کای 2 Chi-Square به شما چه می گوید؟

دو نوع اصلی از آزمون‌های مجذور کای وجود دارد: آزمون استقلال (independence)، که یک سؤال از رابطه را مطرح می‌کند، مانند «آیا بین جنسیت دانش‌آموز و انتخاب رشته رابطه وجود دارد؟»؛ و آزمون خوب بودن تناسب یا برازش (Goodness of fit)، که چیزی شبیه به “چقدر سکه در دست من با سکه از لحاظ نظری منصفانه مطابقت دارد؟”

تجزیه و تحلیل کای دو برای متغیرهای طبقه‌بندی اعمال می‌شود و به ویژه زمانی مفید است که آن متغیرها اسمی باشند (جایی که ترتیب مهم نیست، مانند وضعیت تاهل یا جنسیت).

آزمون استقلال Independence Test

هنگام در نظر گرفتن جنسیت دانشجو و انتخاب رشته، می توان از آزمون χ2 برای استقلال استفاده کرد. برای انجام این آزمون، محقق داده‌های مربوط به دو متغیر انتخابی (جنسیت و دروس انتخابی) را جمع‌آوری می‌کند و سپس فراوانی‌هایی را که دانش‌آموزان دختر و پسر در بین کلاس‌های پیشنهادی انتخاب می‌کنند با استفاده از فرمول بالا و جدول آماری χ2 مقایسه می‌کند.

اگر هیچ رابطه ای بین جنسیت و انتخاب رشته وجود نداشته باشد (یعنی مستقل باشند)، باید انتظار داشت که فرکانس های واقعی که در آن دانش آموزان دختر و پسر هر درس ارائه شده را انتخاب می کنند تقریباً برابر باشد، یا برعکس، نسبت زن و مرد. دانشجویان در هر دوره انتخابی باید تقریباً برابر با نسبت دانشجویان دختر و پسر در نمونه باشند.

یک آزمون χ2 برای استقلال می تواند به ما بگوید که چقدر احتمال دارد که شانس تصادفی بتواند هر تفاوت مشاهده شده بین فرکانس های واقعی در داده ها و این انتظارات نظری را توضیح دهد.

آزمون برازش یا خوب بودن تناسب Goodness-of-Fit Test

χ2 راهی برای آزمایش اینکه چگونه یک نمونه از داده ها با ویژگی های (معلوم یا فرضی) جمعیت بزرگتری که نمونه برای نمایش آن در نظر گرفته شده است مطابقت دارد، ارائه می دهد. این به عنوان حسن تناسب شناخته می شود.

اگر داده‌های نمونه با ویژگی‌های مورد انتظار جامعه مورد علاقه ما مطابقت نداشته باشد، نمی‌خواهیم از این نمونه برای نتیجه‌گیری درباره جمعیت بزرگ‌تر استفاده کنیم.

• برازش چیست؟

4- مثال از آزمون کای 2

به عنوان مثال، یک سکه خیالی با شانس دقیق 50/50 فرود سر یا دم و یک سکه واقعی که 100 بار پرتاب می کنید را در نظر بگیرید. اگر این سکه عادلانه باشد، احتمال فرود در هر دو طرف نیز برابر خواهد بود و نتیجه مورد انتظار از پرتاب 100 سکه این است که سرها 50 بار و دم ها 50 بار بالا می آیند.

در این مورد، χ2 می تواند به ما بگوید که نتایج واقعی 100 چرخش سکه در مقایسه با مدل نظری که یک سکه منصفانه نتایج 50/50 را می دهد چقدر خوب است. پرتاب واقعی می تواند 50/50، یا 60/40، یا حتی 90/10 باشد. هر چه نتایج واقعی 100 پرتاب از 50/50 دورتر باشد، تناسب این مجموعه پرتاب‌ها با انتظارات نظری 50/50 کمتر است، و به احتمال زیاد می‌توان نتیجه گرفت که این سکه در واقع یک سکه منصفانه نیست.

5- چه موقع از تست کای دو استفاده نماییم؟

آزمون خی دو برای کمک به تعیین اینکه آیا نتایج مشاهده شده مطابق با نتایج مورد انتظار هستند و برای رد این که مشاهدات ناشی از شانس هستند، استفاده می شود.

زمانی که داده های مورد تجزیه و تحلیل از نمونه تصادفی باشند و زمانی که متغیر مورد نظر یک متغیر طبقه بندی شده باشد، آزمون کای اسکوئر برای این کار مناسب است. یک متغیر طبقه‌ای، متغیری است که شامل انتخاب‌هایی مانند نوع ماشین، مسابقه، میزان تحصیلات، مرد یا زن، یا میزان دوست داشتن یک کاندیدای سیاسی (از خیلی تا خیلی کم) است.

این نوع داده ها اغلب از طریق پاسخ های نظرسنجی یا پرسشنامه جمع آوری می شوند. بنابراین، تجزیه و تحلیل چی اسکوئر اغلب در تجزیه و تحلیل این نوع داده ها مفید است.

6- نحوه انجام آزمون کای 2

چه در حال انجام یک تست تناسب اندام یا یک تست استقلال هستید، این مراحل اساسی است:

• جدولی از فرکانس های مشاهده شده و مورد انتظار ایجاد کنید.
• از فرمول برای محاسبه مقدار خی دو استفاده کنید.
• مقدار بحرانی chi-square را با استفاده از جدول مقادیر chi-square یا نرم افزار آماری پیدا کنید.
• تعیین کنید که آیا مقدار خی دو یا مقدار بحرانی بزرگتر از این دو است.
• رد یا قبول فرضیه صفر.

7- محدودیت های آزمون کای دو

آزمون مجذور کای به حجم نمونه حساس است. روابط زمانی که صرفاً به دلیل استفاده از نمونه بسیار بزرگ نباشد، ممکن است مهم به نظر برسند.
علاوه بر این، آزمون کای دو نمی تواند تعیین کند که آیا یک متغیر با متغیر دیگر رابطه علی دارد یا خیر. فقط می تواند مشخص کند که آیا دو متغیر به هم مرتبط هستند یا خیر.

8- سوالات متداول

تست Chi-square برای چه مواردی استفاده می شود؟

مجذور کای یک آزمون آماری است که برای بررسی تفاوت بین متغیرهای طبقه بندی شده از یک نمونه تصادفی به منظور قضاوت در مورد خوب بودن برازش بین نتایج مورد انتظار و مشاهده شده استفاده می شود.

چه کسی از مجذور کای استفاده می کند؟

از آنجایی که chi-square برای متغیرهای طبقه‌بندی کاربرد دارد، بیشتر توسط محققانی که داده‌های پاسخ نظرسنجی را مطالعه می‌کنند، استفاده می‌شود. این نوع تحقیقات می تواند از جمعیت شناسی گرفته تا تحقیقات مصرف کننده و بازاریابی تا علوم سیاسی و اقتصاد را شامل شود.

آیا زمانی که متغیر مستقل اسمی یا ترتیبی است از آزمون کای 2 استفاده می شود؟

متغیر اسمی یک متغیر طبقه‌بندی است که با کیفیت متفاوت است، اما ترتیب عددی آن می‌تواند بی‌ربط باشد. به عنوان مثال، پرسیدن رنگ مورد علاقه از کسی یک متغیر اسمی ایجاد می کند. از سوی دیگر، پرسیدن سن یک فرد، مجموعه‌ای از داده‌ها را تولید می‌کند. مجذور کای را می توان به بهترین نحو برای داده های اسمی اعمال کرد.

جمع بندی
دو نوع تست کای دو وجود دارد: تست استقلال و تست برازش. هر دو برای تعیین اعتبار یک فرضیه یا یک فرض استفاده می شوند. نتیجه شواهدی است که می توان از آن برای تصمیم گیری استفاده کرد. مثلا:

در آزمون استقلال، یک شرکت ممکن است بخواهد ارزیابی کند که آیا محصول جدیدش، یک مکمل گیاهی که وعده افزایش انرژی را به مردم می دهد، به افرادی که به احتمال زیاد علاقه مند هستند، می رسد یا خیر. در وب سایت های مرتبط با ورزش و تناسب اندام تبلیغ می شود، با این فرض که افراد فعال و آگاه به سلامت بیشتر احتمال دارد آن را خریداری کنند. این یک نظرسنجی گسترده انجام می دهد که هدف آن ارزیابی علاقه به محصول بر اساس گروه جمعیتی است. این نظرسنجی نشان می‌دهد که هیچ ارتباطی بین علاقه به این محصول و افرادی که به سلامت بیشتر اهمیت می‌دهند وجود ندارد.

در یک آزمون برازش، یک متخصص بازاریابی در نظر دارد محصول جدیدی را عرضه کند که این شرکت معتقد است برای زنان بالای 45 سال غیرقابل مقاومت خواهد بود. این شرکت پانل های تست محصول را از 500 خریدار بالقوه محصول انجام داده است. متخصص بازاریابی اطلاعاتی در مورد سن و جنسیت پنل‌های آزمایشی دارد، این اجازه می‌دهد تا یک تست کای 2 ساخته شود که توزیع بر اساس سن و جنسیت افرادی را که گفته‌اند محصول را خریداری می‌کنند نشان می‌دهد. نتیجه نشان می دهد که آیا محتمل ترین خریدار یک زن بالای 45 سال است یا خیر. اگر آزمایش نشان دهد که مردان بالای 45 سال یا زنان بین 18 تا 44 سال به همان اندازه احتمال خرید محصول را دارند، متخصص بازاریابی تبلیغات و قرار دادن محصول برای جذب این گروه وسیع تر از مشتریان را انجام خواهد داد.