آزمون کولموگروف اسميرنف چیست؟
- آزمون کولموگروف اسمیرنوف چیست؟
- ویژگی های آزمون کولموگروف اسمیرنف
- توزیع کولموگروف
- فرمول آزمون کولموگروف اسمیرنف
- اهمیت و کاربرد آزمون کولموگروف اسمیرنوف در تحلیل داده
- نحوه عملکرد آزمون کولموگروف اسمیرنوف
- چه زمانی از آزمون کولموگروف اسمیرنوف استفاده می شود؟
- تفاوت بین آزمون کولموگروف اسمیرنف تک نمونه ای و دو نمونه ای چیست؟
- آزمون یک نمونه ای کولموگروف-اسمیرنوف
- آزمون دو نمونه ای کولموگروف-اسمیرنوف
- آزمون کولموگروف اسمیرنوف چندبعدی
- توزیع کولموگروف و آزمون برازش
- چگونه توزیع کولموگروف ایجاد می شود؟
- نحوه اجرای آزمون کولموگروف اسمیرنف در SPSS
- آیا آزمون کولموگروف اسمیرنف می تواند برای پایش تغییرات مدل در طول زمان استفاده شود؟
- در چه مواردی آزمون کولموگروف اسمیرنف به شاخص پایداری جمعیت، واگرایی KL و واگرایی JS ترجیح داده می شود؟
- کاربرد های آزمون کولموگروف اسمیرنوف
- محدودیت های آزمون کولموگروف اسمیرنوف
چکیده مقاله:
آزمون کولموگروف اسمیرنف (Kolmogorov-Smirnov Test) یکی از آزمون های مهم و پرکاربرد در آمار است که برای بررسی همگونی یک توزیع تجربی با یک توزیع نظری مشخص یا مقایسه دو توزیع تجربی به کار می رود. این آزمون مبتنی بر مقایسه بیشترین تفاوت مطلق میان توزیع تجربی و توزیع نظری یا دو توزیع تجربی است و به صورت غیرپارامتریک عمل می کند. این ویژگی آن را برای تحلیل داده هایی که از پیش فرض های خاصی همچون نرمال بودن یا همسانی واریانس پیروی نمی کنند، بسیار مناسب می سازد. در نتیجه، آزمون کولموگروف-اسمیرنوف در حوزه های گوناگونی از جمله علوم آماری، اقتصاد، مهندسی و علوم اجتماعی بطور گسترده مورد استفاده قرار میگیرد.
کاربرد اصلی این آزمون، ارزیابی نیکویی برازش یک توزیع دادهها به یک مدل نظری است. برای مثال، در تحلیل های آماری اغلب این سؤال مطرح می شود که آیا داده های نمونه از توزیع نرمال یا توزیع خاص دیگری پیروی می کنند یا خیر. آزمون کولموگروف-اسمیرنوف به دلیل سادگی در محاسبه و تفسیر، ابزاری قدرتمند برای پاسخ به این سؤال فراهم میکند. این آزمون همچنین میتواند در تحلیل مقایسه ای، برای بررسی تفاوت بین دو مجموعه داده یا دو گروه مورد مطالعه، مورد استفاده قرار گیرد. مزیت دیگر این آزمون، کاربرد آن برای داده هایی با توزیع نامعلوم است که آن را به یکی از ابزارهای اساسی در تحلیل آماری تبدیل کرده است.
آزمون کولموگروف اسمیرنوف یکی از پرکاربرد ترین ابزار های آماری برای بررسی تطابق داده ها با توزیع های نظری و مقایسه دو نمونه مستقل است. این آزمون توانایی سنجش بیشترین اختلاف بین توابع توزیع تجمعی تجربی و توزیع نظری یا توزیع نمونه دیگر را دارد و به محققان، تحلیلگران داده و مهندسان کمک می کند تا از انطباق یا اختلاف داده ها با الگو های فرض شده اطمینان حاصل کنند. در این مقاله، ما به بررسی کامل این آزمون، شامل آزمون یک نمونه ای، آزمون دو نمونه ای، تعمیم به داده های چندبعدی، کاربرد های عملی و محدودیت های آن خواهیم پرداخت. همچنین، مثال های عملی در محیط پایتون ارائه شده است تا نحوه اجرای آزمون به صورت گام به گام برای خواننده روشن شود. هدف این مقاله ارائه یک راهنمای جامع و کاربردی است تا مخاطبان بتوانند از آزمون کولموگروف اسمیرنوف در تحلیل داده ها، کنترل کیفیت، بررسی فرضیات آماری و تصمیم گیری های علمی استفاده کنند.
آزمون کولموگروف اسمیرنوف (Kolmogorov-Smirnov Test)
آزمون کولموگروف اسمیرنوف چیست؟

آزمون کولموگروف اسمیرنوف چیست؟
این آزمون یکی از روش های کاملاً موثر برای تعیین این است که آیا دو نمونه به طور معناداری با یکدیگر متفاوت هستند یا خیر. این آزمون معمولاً برای بررسی یکنواختی اعداد تصادفی مورد استفاده قرار می گیرد. یکنواختی یکی از مهم ترین ویژگی ها در هر تولید کننده عدد تصادفی است و این آزمون می تواند برای بررسی این ویژگی به کار رود.
این آزمون بسیار انعطاف پذیر است و می توان از آن برای ارزیابی این موضوع استفاده کرد که آیا دو توزیع احتمال یک بعدی زمینه ای با یکدیگر تفاوت دارند یا خیر. Kolmogorov-Smirnov Test ابزاری موثر برای تعیین اهمیت آماری تفاوت ها بین دو مجموعه داده به شمار می رود. این آزمون در زمینه های مختلفی مانند آمار، تحلیل داده و کنترل کیفیت ارزشمند است، جایی که نیاز به بررسی دقیق یکنواختی اعداد تصادفی یا تفاوت های توزیعی بین مجموعه داده ها وجود دارد.
آزمون کولموگروف اسمیرنف (Kolmogorov-Smirnov Test) که با نام اختصاری KS Test یا K-S Test شناخته می شود، یک آزمون آماری غیرپارامتری است که برای مقایسه دو توزیع استفاده می شود. هدف از این آزمون، تعیین این موضوع است که آیا دو توزیع مورد مقایسه از یک توزیع زیربنایی مشابه گرفته شده اند یا خیر.
در کاربردهای معمول یادگیری ماشین، دو توزیع (A و B) برای مقایسه مورد استفاده قرار می گیرند. برای مثال، توزیع A می تواند مربوط به یک ویژگی مانند مانده حساب در داده های آموزش مدل باشد و توزیع B همان ویژگی در بازه زمانی مشخصی از داده های تولید (مانند داده های روزانه یا ساعتی) باشد. به عنوان یک سازنده مدل، شما می خواهید بدانید که آیا مدل اجرا شده با داده هایی استفاده می شود که با داده های آموزش متفاوت هستند یا خیر. آزمون کولموگروف اسمیرنف ابزاری برای مقایسه این توزیع ها است.
ویژگی های آزمون کولموگروف اسمیرنف
- غیرپارامتری بودن: این آزمون نیازی به فرض توزیع خاصی (مانند نرمال یا دو جمله ای) ندارد و برای هر نوع توزیعی قابل استفاده است.
- محدودیت ها: آزمون K-S فقط برای متغیرهای عددی (مانند اعداد صحیح یا اعشاری) قابل استفاده است و برای متغیرهای دسته بندی (Categorical) مناسب نمی باشد.
توزیع کولموگروف
توزیع کولموگروف که معمولاً با نماد D نشان داده می شود، تابع توزیع تجمعی (CDF) بیشینه اختلاف بین تابع توزیع تجربی نمونه و تابع توزیع تجمعی مرجع را نمایش می دهد.
تابع توزیع احتمالی (PDF) خود توزیع کولموگروف به شکل تحلیلی ساده بیان نمی شود. به جای آن، معمولاً از جداول آماری یا نرم افزارهای آماری برای به دست آوردن مقادیر بحرانی آزمون استفاده می شود. این توزیع تحت تأثیر اندازه نمونه است و مقادیر بحرانی به سطح اهمیت انتخاب شده برای آزمون بستگی دارند.
فرمول تابع توزیع کولموگروف به صورت زیر است:
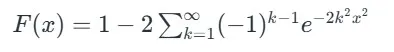
فرمول تابع توزیع کولموگروف
که در آن:
- n اندازه نمونه است.
- x آماره کولموگروف-اسمیرنوف نرمال شده است.
- k شاخص جمع در سری می باشد.
فرمول آزمون کولموگروف اسمیرنف
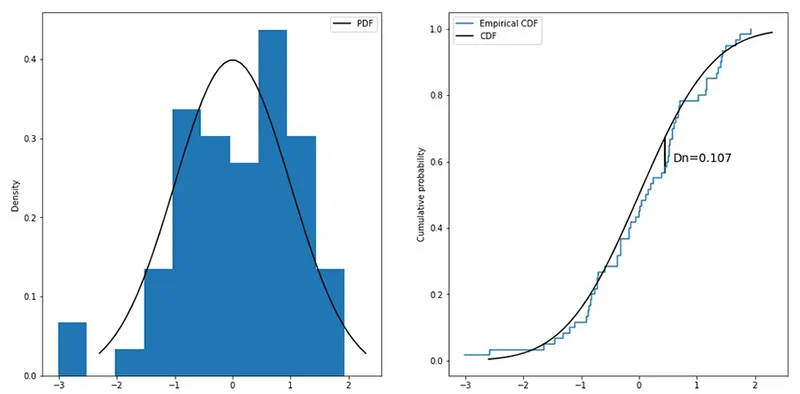
آمار آزمون کولموگروف اسمیرنف به صورت حداکثر تفاوت بین توزیع تجمعی دو مجموعه داده (CDF) تعریف می شود. در تنظیمات یادگیری ماشین، این توزیع تجمعی ها اغلب به صورت تجربی از نمونه داده ها به دست می آیند و به آنها eCDF گفته می شود.

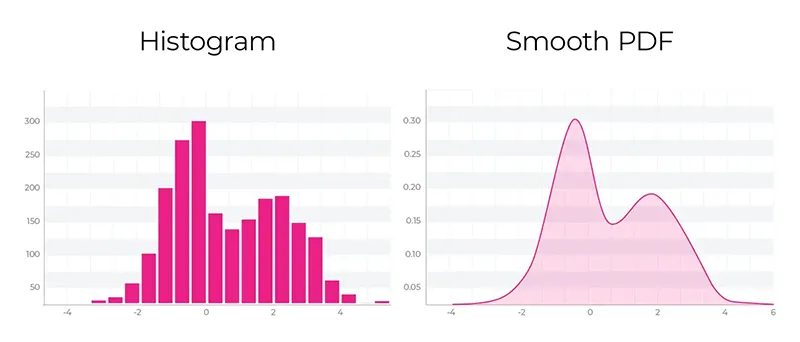
داده هایی که برای یک متغیر یا ویژگی در آموزش یا تولید جمع آوری می کنید ممکن است شبیه توزیع های بالا باشد. یک CDF تجربی با مرتب کردن داده ها بر اساس مقدار و ایجاد یک نمودار تکه تکه ایجاد می شود.
کد ساده برای محاسبه توزیع تجمعی (CDF) در پایتون
برای محاسبه توزیع تجمعی تجربی، داده ها بر اساس مقدار مرتب شده و یک نمودار پله ای ایجاد می شود. در ادامه، کدی ساده برای این کار ارائه شده است:
CDF یک جمع تجمعی گام به گام در امتداد محدوده متغیر داده ایجاد می کند.
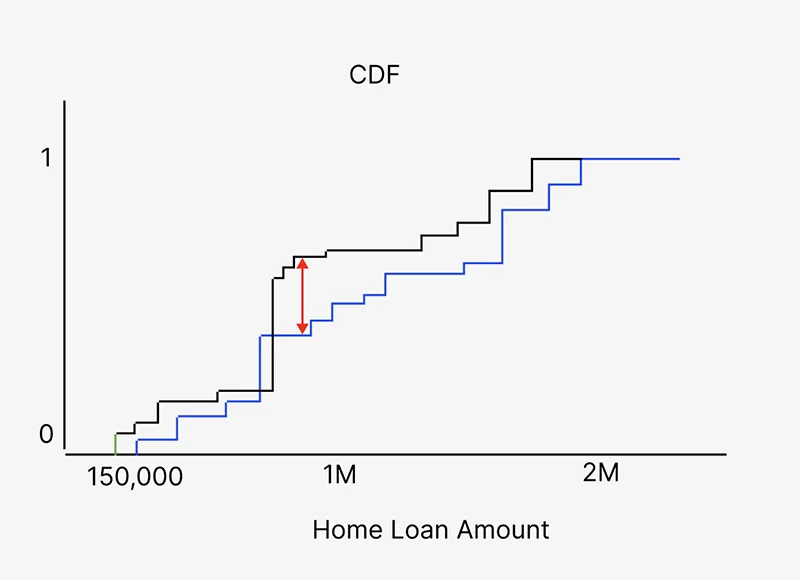
در مثال بالا، می توان eCDF موجودی حساب ویژگی از تولید را در مقایسه با موجودی حساب eCDF از آموزش مشاهده کرد. eCDF تکه ای آبی داده های آموزشی است در حالی که خط سیاه داده های تولید است. فلش قرمز نشان دهنده آمار آزمون K-S، حداکثر تفاوت بین eCDF ها است.
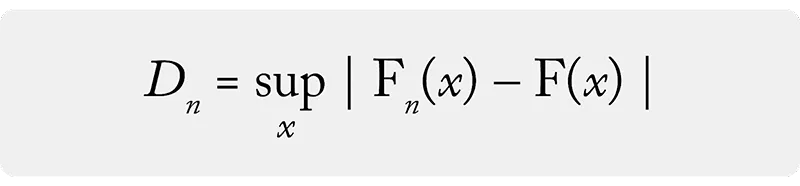
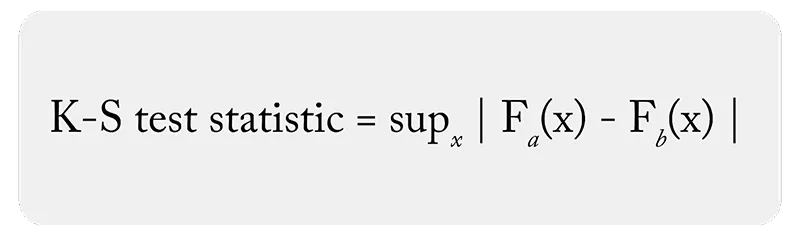
اهمیت و کاربرد آزمون کولموگروف اسمیرنوف در تحلیل داده
Kolmogorov-Smirnov Test ابزار قدرتمندی برای تحلیل داده های آماری است. این آزمون نه تنها برای بررسی یکنواختی داده های تصادفی مفید است، بلکه می تواند در تعیین اینکه دو مجموعه داده از نظر توزیع با یکدیگر تفاوت دارند یا نه، کمک شایانی کند. برای مثال، در تحقیقات علمی، کنترل کیفیت محصولات یا بررسی فرآیندهای تولید، این آزمون می تواند اختلافات آماری را با دقت بالایی نشان دهد.
یکی از ویژگی های مهم این آزمون این است که نیاز به مفروضات سختگیرانه درباره نوع توزیع داده ها ندارد. به همین دلیل، این آزمون برای داده های واقعی که ممکن است توزیع آن ها ناشناخته باشد، بسیار مناسب است.
نحوه عملکرد آزمون کولموگروف اسمیرنوف
Kolmogorov-Smirnov Test با یک روند مرحله ای مشخص انجام می شود که در ادامه به تفصیل توضیح داده شده است.
-
فرموله کردن فرضیات
در اولین مرحله، فرضیات آماری برای آزمون مشخص می شوند:
- فرض صفر: نمونه مورد بررسی از یک توزیع مشخص پیروی می کند.
- فرض جایگزین: نمونه مورد بررسی از توزیع مشخص شده پیروی نمی کند.
این گام پایه و اساس تصمیم گیری آماری برای تحلیل داده ها را فراهم می کند.
-
انتخاب توزیع مرجع
در این مرحله یک توزیع نظری برای مقایسه با نمونه انتخاب می شود. این توزیع می تواند نرمال، نمایی یا سایر توزیع های رایج باشد. انتخاب توزیع مرجع معمولاً بر اساس انتظارهای نظری یا دانش پیشین انجام می شود تا بتوان مقایسه دقیقی با داده های واقعی داشت.
-
محاسبه آماره آزمون (D)
برای آزمون یک نمونه ای کولموگروف-اسمیرنوف، آماره آزمون D بیشترین انحراف عمودی بین تابع توزیع تجربی نمونه (EDF) و تابع توزیع تجمعی مرجع (CDF) را نشان می دهد.
برای آزمون دو نمونه ای کولموگروف-اسمیرنوف، آماره آزمون D اختلاف بین EDF دو نمونه مستقل را مقایسه می کند تا مشخص شود آیا تفاوت معناداری بین توزیع های آن ها وجود دارد یا خیر.
-
تعیین مقدار بحرانی یا مقدار P
پس از محاسبه آماره آزمون، این مقدار با مقدار بحرانی از جدول توزیع کولموگروف-اسمیرنوف مقایسه می شود یا به طور رایج تر، مقدار P محاسبه می شود.
- اگر مقدار P کمتر از سطح معنی داری انتخاب شده (معمولاً ۰.۰۵) باشد، فرض صفر رد می شود. این نشان می دهد که توزیع نمونه با توزیع مشخص شده مطابقت ندارد.
-
تفسیر نتایج
در صورت رد فرض صفر، می توان نتیجه گرفت که شواهد کافی برای نشان دادن تفاوت بین توزیع نمونه و توزیع نظری وجود دارد. به عبارت دیگر، فرض جایگزین پذیرفته می شود و نشان دهنده وجود اختلاف معنادار آماری است.
چه زمانی از آزمون کولموگروف اسمیرنوف استفاده می شود؟
هدف اصلی از استفاده از Kolmogorov-Smirnov Test بررسی این است که آیا دو نمونه مورد بررسی از یک نوع توزیع پیروی می کنند یا شکل توزیع آن ها مشابه است یا خیر. این آزمون به تحلیل تفاوت ها و شباهت های توزیعی بین داده ها کمک می کند.
-
مقایسه توزیع های احتمالی
این آزمون برای ارزیابی این موضوع استفاده می شود که آیا دو نمونه یک توزیع احتمالی مشابه دارند یا نه. در واقع، این آزمون به ما امکان می دهد تا بفهمیم داده ها از نظر ساختار توزیعی تا چه حد با هم هماهنگ هستند.
-
مقایسه شکل توزیع ها
اگر فرض شود که شکل یا توزیع احتمالی دو نمونه مشابه است، آزمون بیشترین اختلاف مطلق بین توزیع تجمعی احتمالی دو تابع را اندازه گیری می کند. این گام کمک می کند تا تفاوت های جزئی یا کلی بین نمونه ها شناسایی شود.
-
بررسی تفاوت های توزیعی
این آزمون بیشترین اختلاف بین توزیع های تجمعی احتمالی را کمی می کند. مقدار بالاتر نشان دهنده تفاوت بیشتر در شکل توزیع ها است. به عبارت دیگر، هر چه اختلاف تجمعی بیشتر باشد، نمونه ها شباهت کمتری به یکدیگر دارند.
-
انواع آزمون های فرضیه
ارزیابی شکل داده های نمونه معمولاً از طریق آزمون فرضیه انجام می شود. این آزمون ها به دو دسته کلی تقسیم می شوند:
- آزمون پارامتریک: فرضیات مشخصی درباره توزیع داده ها دارد.
- آزمون غیرپارامتریک: برای داده هایی که فرضیات توزیعی مشخصی ندارند مناسب است. کولموگروف-اسمیرنوف در دسته آزمون های غیرپارامتریک قرار می گیرد و به همین دلیل برای انواع مختلف داده ها کاربرد دارد.
تفاوت بین آزمون کولموگروف اسمیرنف تک نمونه ای و دو نمونه ای چیست؟
آزمون کولموگروف اسمیرنف دو نوع دارد: آزمون تک نمونه ای و آزمون دو نمونه ای (این دو نباید با یک طرفه و دو طرفه اشتباه گرفته شوند). مثال های قبلی مربوط به آزمون دو نمونه ای است که در آن هر دو توزیع تجربی هستند و از داده های واقعی گرفته شده اند.
- آزمون دو نمونه ای: eCDF توزیع A با eCDF توزیع B مقایسه می شود.
- آزمون تک نمونه ای: eCDF توزیع A با CDF توزیع B مقایسه می شود.
آزمون تک نمونه ای تقریبا هرگز در یادگیری ماشین تولیدی استفاده نمی شود. این نوع آزمون زمانی به کار می رود که بخواهید یک نمونه تجربی را با یک توزیع نظری پارامتری مقایسه کنید. برای مثال، ممکن است بخواهید بررسی کنید که آیا توزیع مانده حساب در داده های آموزشی (توزیع A) به صورت نرمال توزیع شده است (توزیع B).
آزمون یک نمونه ای کولموگروف-اسمیرنوف
آزمون یک نمونه ای کولموگروف-اسمیرنوف برای تعیین این استفاده می شود که آیا یک نمونه از توزیع خاصی پیروی می کند یا خیر. این آزمون به ویژه زمانی کاربرد دارد که فرض نرمال بودن داده ها مورد سوال است یا با نمونه های کوچک سر و کار داریم.
آماره آزمون که با Dn نشان داده می شود، بیشترین اختلاف بین دو تابع توزیع تجمعی را اندازه گیری می کند.
تابع توزیع تجربی (Empirical Distribution Function)
تابع توزیع تجربی در مقدار x نشان دهنده نسبت داده هایی است که کمتر یا مساوی x هستند. این تابع به شکل زیر تعریف می شود:
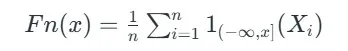
تابع توزیع تجربی در آزمون یک نمونه ای کولموگروف-اسمیرنوف
که در آن:
- n تعداد مشاهدات در نمونه است.
- Xi نمایانگر هر مشاهده مستقل در نمونه می باشد.
یک تابع شاخص است که اگر
باشد، مقدار آن ۱ و در غیر این صورت ۰ است.
به عبارت ساده، برای هر مشاهده اگر شرط برقرار باشد ۱ و در غیر این صورت ۰ محسوب می شود.
آماره کولموگروف-اسمیرنوف
آماره کولموگروف-اسمیرنوف برای یک تابع توزیع تجمعی نظری F(x) به شکل زیر تعریف می شود:
فرمول آماره کولموگروف-اسمیرنوف برای یک تابع توزیع تجمعی نظری F(x)در آزمون یک نمونه ای
که در آن:
- sup به معنای بیشینه مقدار در تمام مقادیر ممکن x است.
- F(x) تابع توزیع تجمعی نظری است.
- Fn(x) تابع توزیع تجمعی تجربی نمونه است که همان طور که در بالا توضیح داده شد محاسبه می شود.
این آماره نشان می دهد که بیشترین اختلاف بین داده های واقعی نمونه و توزیع نظری چقدر است. هر چه این اختلاف بزرگ تر باشد، شواهد بیشتری وجود دارد که نمونه از توزیع فرض شده پیروی نمی کند.
مثال عملی آزمون یک نمونه ای کولموگروف-اسمیرنوف
فرض کنید یک نمونه شامل n مشاهده داریم و می خواهیم بررسی کنیم آیا این نمونه از یک توزیع نرمال با میانگین μ و انحراف معیار σ پیروی می کند یا خیر. فرض صفر این است که نمونه از توزیع مشخص شده پیروی می کند.
مراحل انجام آزمون به شکل زیر است:
- محاسبه تابع توزیع تجربی (EDF)
برای هر مقدار x در نمونه، نسبت داده هایی که کمتر یا مساوی x هستند محاسبه می شود تا تابع توزیع تجربی ساخته شود.
- مشخص کردن توزیع مرجع
در این مثال، توزیع مرجع همان توزیع نرمال با میانگین μ و انحراف معیار σ است. تابع توزیع تجمعی این توزیع به عنوان مرجع برای مقایسه با نمونه استفاده می شود.
- محاسبه آماره کولموگروف-اسمیرنوف
آماره آزمون Dn محاسبه می شود که نشان دهنده بیشترین اختلاف بین تابع توزیع تجربی نمونه و تابع توزیع تجمعی نظری است.
- مقایسه با مقدار بحرانی یا P-value
مقدار آماره آزمون یا مقدار P با سطح معنی داری انتخاب شده مقایسه می شود. اگر آماره آزمون بزرگ تر از مقدار بحرانی یا P-value کمتر از سطح معنی داری باشد، فرض صفر رد می شود.
مثال در پایتون
خروجی
در این مثال:
- آماره آزمون نسبتاً کوچک است (۰.۱۰۳) که نشان می دهد تابع توزیع تجربی و تابع توزیع تجمعی نظری به یکدیگر نزدیک هستند.
- از آنجا که P-value )۰.۲۱۸ ( بیشتر از سطح معنی داری ۰.۰۵ است، فرض صفر رد نمی شود.
- بنابراین نمی توان نتیجه گرفت که نمونه از توزیع نرمال مشخص شده پیروی نمی کند.
آزمون دو نمونه ای کولموگروف-اسمیرنوف
آزمون دو نمونه ای کولموگروف-اسمیرنوف برای مقایسه دو نمونه مستقل استفاده می شود تا مشخص شود آیا این دو نمونه از یک توزیع مشابه پیروی می کنند یا خیر. این آزمون توزیع آزاد است و بیشترین اختلاف عمودی بین توابع توزیع تجربی (EDF) دو نمونه را ارزیابی می کند.
تابع توزیع تجربی (EDF)
تابع توزیع تجربی در مقدار x در هر نمونه، نشان دهنده نسبت مشاهداتی است که کمتر یا مساوی x هستند. به صورت ریاضی، EDF ها برای دو گروه به شکل زیر تعریف می شوند:
برای گروه اول:
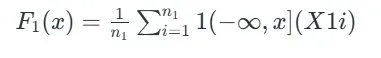
برای گروه اول آزمون دو نمونه ای کولموگروف-اسمیرنوف Xتابع توزیع تجربی در مقدار
برای گروه دوم:
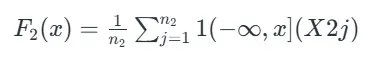
برای گروه دوم آزمون دو نمونه ای کولموگروف-اسمیرنوف Xتابع توزیع تجربی در مقدار
که در آن:
- n1 و n2 اندازه نمونه های گروه اول و دوم هستند.
- X1i و X2j مشاهدات مستقل در نمونه های مربوطه هستند.
توابع شاخص هستند که اگر مقدار مشاهده کمتر یا مساوی x باشد، برابر با ۱ و در غیر این صورت ۰ هستند.
تابع توزیع تجربی نشان می دهد چه درصدی از مشاهدات نمونه مورد نظر کمتر یا مساوی یک مقدار مشخص است.
آماره کولموگروف-اسمیرنوف
آماره آزمون برای دو نمونه مستقل به شکل زیر تعریف می شود:
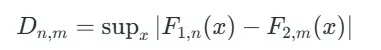
آماره کولموگروف-اسمیرنوف برای آزمون دو نمونه ای کولموگروف-اسمیرنوف
که در آن:
- Sup به معنای بیشینه مقدار برای تمام مقادیر ممکن x است.
- F1(x) و F2(x) توابع توزیع تجمعی تجربی (ECDF) دو نمونه هستند.
هر ECDF نشان می دهد چه نسبتی از مشاهدات نمونه مربوطه کمتر یا مساوی یک مقدار مشخص x هستند. آماره آزمون بیشترین اختلاف بین این دو ECDF را نشان می دهد و هرچه مقدار آن بیشتر باشد، شواهد قوی تری وجود دارد که توزیع های دو نمونه با یکدیگر متفاوت هستند.
مثال عملی آزمون دو نمونه ای کولموگروف-اسمیرنوف
برای انجام آزمون دو نمونه ای کولموگروف-اسمیرنوف می توان از تابع ks_2samp در کتابخانه scipy.stats در پایتون استفاده کرد. این تابع آماره کولموگروف-اسمیرنوف را برای دو نمونه محاسبه می کند تا مشخص شود آیا دو نمونه از توزیع متفاوتی پیروی می کنند یا خیر.
فرض صفر این است که دو نمونه از یک توزیع مشابه پیروی می کنند. تصمیم گیری بر اساس مقایسه P-value با سطح معنی داری انتخاب شده (مثلاً ۰.۰۵) انجام می شود. اگر P-value کمتر از سطح معنی داری باشد، فرض صفر رد می شود و نشان می دهد که دو نمونه از توزیع های متفاوتی آمده اند.
مثال کد پایتون
خروجی
در این مثال:
- آماره آزمون نسبتا بزرگ است (۰.۳۵۸) که نشان می دهد اختلاف قابل توجهی بین توزیع دو نمونه وجود دارد.
- مقدار P-value بسیار کوچک است (۹.۹۴×۱۰^-۷)، که شواهد قوی علیه فرض صفر ارائه می دهد.
- بنابراین نتیجه می گیریم که دو نمونه از توزیع های متفاوتی آمده اند.
آزمون کولموگروف اسمیرنوف چندبعدی
آزمون کولموگروف اسمیرنوف در فرم سنتی خود برای داده های یک بعدی طراحی شده است و در آن تشابه بین تابع توزیع تجربی (EDF) و یک توزیع نظری یا یک توزیع تجربی دیگر در طول یک محور بررسی می شود. با این حال، وقتی داده ها چند بعدی هستند، تعمیم آزمون کولموگروف اسمیرنوف پیچیده تر می شود.
در زمینه داده های چندبعدی، مفهوم آماره کولموگروف-اسمیرنوف می تواند برای ارزیابی اختلافات در طول ابعاد مختلف تطبیق داده شود. این تطبیق معمولاً شامل در نظر گرفتن بیشترین فاصله یا اختلاف بین توابع توزیع تجمعی در هر بعد است. تعمیم عمومی آزمون KS به ابعاد بالاتر به عنوان آزمون کولموگروف اسمیرنوف n بعدی شناخته می شود.
هدف این آزمون بررسی این است که آیا دو نمونه چندبعدی از یک توزیع مشابه پیروی می کنند یا خیر. آماره آزمون به تابع بیشترین اختلاف در توابع توزیع تجمعی در هر بعد تبدیل می شود.
توزیع کولموگروف و آزمون برازش
آمار آزمون کولموگروف اسمیرنف، که از حداکثر تفاوت بین دو eCDF به دست می آید، فقط یک نمونه را نشان می دهد. توزیع کولموگروف، توزیع مقادیر آماره آزمون K-S است که در صورت گرفتن تعداد زیادی نمونه از یک توزیع واحد، به دست می آید.
چگونه توزیع کولموگروف ایجاد می شود؟
برای ایجاد این توزیع:
- داده ها را به صورت بوت استرپ بازنمونه گیری کنید یا یک eCDF دیگر جمع آوری کنید.
- این فرآیند را 500 بار تکرار کنید تا 500 eCDF ایجاد شود.
- مقدار K-S را برای هر eCDF محاسبه کنید.
- تمام 500 مقدار K-S را به صورت یک توزیع نمایش دهید.
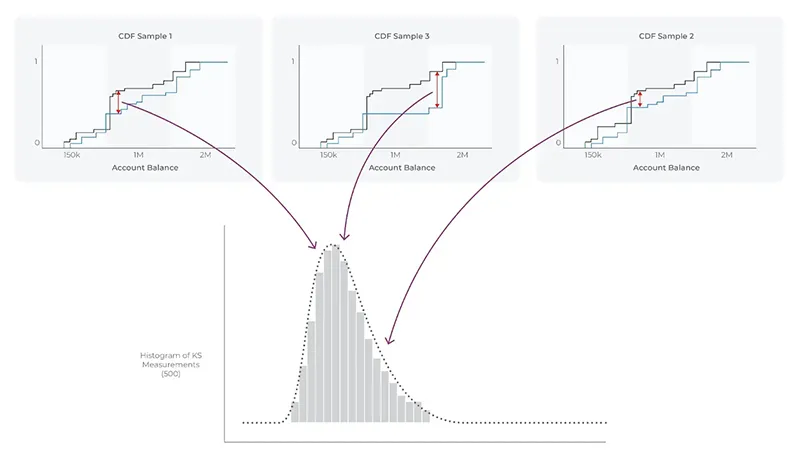
در بالا، توزیع K-S با اندازه های نمونه N به نظر می رسد، هر نمونه ای که گرفته شود، مقدار متفاوتی از K-S خواهد داشت. آندری کولموگروف در مقاله اصلی خود اشاره کرده است که توزیع مقادیر K-S از چندین نمونه، شکلی خاص به خود می گیرد که اکنون به نام توزیع کولموگروف شناخته می شود.
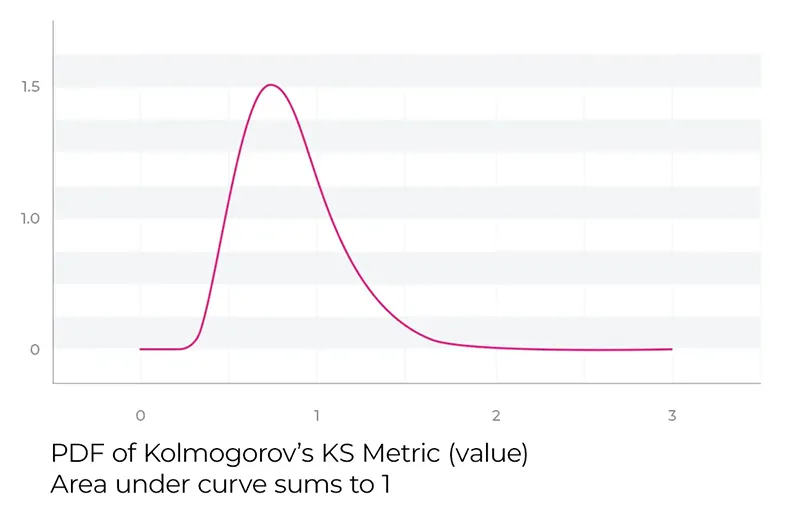
تحلیل توزیع کولموگروف
این توزیع دارای یک معادله با فرم بسته است که فقط به تعداد نمونه های استفاده شده در تولید eCDF وابسته است. توزیع کولموگروف متفاوت از توزیع گوسی است، اما برخی از مفاهیم مشابه مانند p-value را می توان بر آن اعمال کرد.
در پایتون، مقدار p-value در تابع ks_2samp احتمال مشاهده مقدار آماره آزمون K-S را (با فرض توزیع به صورت کولموگروف) تعیین می کند. این آزمون به عنوان آزمون برازش شناخته می شود.
برای ملموس تر کردن این موضوع، می توانید چند مثال زیر را اجرا کنید (کد):
نحوه اجرای آزمون کولموگروف اسمیرنف در SPSS
برای اجرای آزمون کولموگروف اسمیرنف (KS Test) در نرم افزار SPSS، مراحل زیر را دنبال کنید:
- رفتن به منوی تحلیل
از منوی اصلی SPSS، مسیر Analyze → Descriptive Statistics → Explore را انتخاب کنید. - انتقال متغیرها به لیست وابسته
متغیرهایی که می خواهید از نظر نرمال بودن بررسی کنید را به کادر Dependent List منتقل کنید. - اختیاری: بررسی وجود داده های پرت
اگر می خواهید داده های پرت را بررسی کنید، روی گزینه Statistics کلیک کرده و علامت چک کنار گزینه Outliers را فعال کنید. - تنظیم نمودارها
روی Plots کلیک کنید و علامت چک کنار گزینه Histogram و گزینه Normality Plots with tests را فعال کنید. سپس روی Continue کلیک کنید. - تنظیم نحوه مدیریت مقادیر گم شده
روی Options کلیک کنید و مشخص کنید که چگونه مقادیر گم شده مدیریت شوند:- Exclude cases listwise: مواردی که مقادیر گم شده دارند به طور کامل حذف شوند.
- Exclude cases pairwise: میانگین هر متغیر با استفاده از تمام پاسخ های غیر گم شده برای همان متغیر محاسبه شود.
- Report values: این گزینه فقط بر تجزیه و تحلیل متغیرهای عاملی تأثیر می گذارد.
سپس روی Continue کلیک کنید.
- اجرای آزمون KS
روی OK کلیک کنید تا آزمون اجرا شود. - خواندن نتایج
نتایج آزمون را در بخش Tests of Normality بررسی کنید.- ستون Sig مقدار p-value را نمایش می دهد. اگر این مقدار کوچک باشد (مثلا کمتر از 0.05 برای سطح اطمینان 5%)، فرض صفر مبنی بر نرمال بودن داده ها رد می شود.
- مقادیر بزرگ p نشان دهنده نرمال بودن داده ها هستند.
SPSS به طور همزمان نتایج آزمون شاپیرو-ویلک (Shapiro-Wilk Test) را نیز ارائه می دهد. توجه داشته باشید:
- برای نمونه های بزرگ (n ≥ 50)، نتایج آزمون K-S را بررسی کنید.
- برای نمونه های کوچک (n < 50)، از نتایج شاپیرو-ویلک استفاده کنید.
- بررسی داده های پرت
بخش Extreme Values اطلاعاتی درباره داده های پرت ارائه می دهد.
این مراحل به شما کمک می کنند که به سادگی آزمون نرمال بودن داده ها را در SPSS انجام دهید و نتایج قابل اعتمادی به دست آورید.
آیا آزمون کولموگروف اسمیرنف می تواند برای پایش تغییرات مدل در طول زمان استفاده شود؟
بله. در کاربردهای آماری معمول، آزمون کولموگروف اسمیرنف یک مقایسه ثابت بین دو توزیع A و B است. اما در موارد پایش، دانشمندان داده به صورت دوره ای eCDF ها را ایجاد کرده و K-S را اندازه گیری می کنند. پایش آماره K-S در طول زمان می تواند نشان دهنده تغییر در توزیع باشد.
اجرای این فرآیند در عمل برای محیط های عملیاتی یادگیری ماشین بزرگ، چالش هایی دارد. زمانی که یک هشدار رخ می دهد، شناسایی سریع تغییرات و ارتباط آن با داده ها برای مدیریت تعداد زیادی از مدل ها و ویژگی ها حیاتی است.
در چه مواردی آزمون کولموگروف اسمیرنف به شاخص پایداری جمعیت، واگرایی KL و واگرایی JS ترجیح داده می شود؟
بین معیارهای مبتنی بر نظریه اطلاعات (مانند واگرایی JS، PSI و KL) و آزمون کولموگروف اسمیرنف تفاوت های زیادی وجود دارد. یک تفاوت کلیدی این است که محتوای اطلاعاتی بین دو توزیع می تواند تغییر کند، اما آماره آزمون K-S تغییر نکند.
برای مثال، در K-S، تغییر در ترتیب نقاط بالای حداکثر، آماره آزمون را تغییر نمی دهد، مگر اینکه تفاوتی در حداکثر ایجاد شود. اما در معیارهای مبتنی بر نظریه اطلاعات، هرگونه حرکت داده بین دسته ها (bins) تغییراتی در مقدار معیار ایجاد می کند.
کاربرد های آزمون کولموگروف اسمیرنوف
-
بررسی تطابق با توزیع فرض شده (Goodness-of-fit)
آزمون کولموگروف اسمیرنوف می تواند برای بررسی میزان انطباق داده ها با یک توزیع فرض شده استفاده شود. این کاربرد به ویژه برای تعیین این که آیا یک نمونه از یک توزیع خاص مانند توزیع نرمال یا نمایی گرفته شده است یا خیر مفید است. این روش در حوزه های مختلف مانند مالی، مهندسی و علوم طبیعی برای بررسی تطابق داده ها با توزیع پیش بینی شده استفاده می شود، که می تواند در تصمیم گیری، برازش مدل و پیش بینی موثر باشد.
-
مقایسه دو نمونه
این آزمون برای ارزیابی دو مجموعه داده به منظور بررسی اینکه آیا از یک توزیع یکسان آمده اند یا خیر استفاده می شود. این کاربرد در تحلیل تفاوت های آماری بین گروه ها، مقایسه عملکرد شرکت ها در یک آزمایش یا بررسی توزیع دو متغیر خاص اهمیت دارد. این نوع کاربرد بیشتر در علوم اجتماعی، پزشکی و کسب و کار برای بررسی تفاوت های گروهی استفاده می شود.
-
بررسی فرضیه های توزیعی
آزمون کولموگروف اسمیرنوف می تواند برای بررسی فرضیه های مربوط به ویژگی های توزیعی داده ها استفاده شود. برای مثال، بررسی اینکه آیا یک مجموعه داده به صورت نرمال توزیع شده است یا از یک توزیع نظری خاص پیروی می کند. این کاربرد به تایید فرضیات آماری و اعتبارسنجی مدل ها کمک می کند.
-
جایگزین غیرپارامتریک
آزمون KS یک آزمون غیرپارامتریک است و به همین دلیل نیاز به فرضیات خاص درباره شکل یا پارامترهای توزیع ندارد. این ویژگی آن را به جایگزینی مناسب برای آزمون های پارامتریک مانند t-test یا ANOVA تبدیل می کند، مخصوصاً زمانی که داده ها نرمال توزیع نشده اند، واریانس ها ناشناخته یا نابرابر هستند یا اندازه نمونه کوچک است.
محدودیت های آزمون کولموگروف اسمیرنوف
- حساسیت به اندازه نمونه: این آزمون ممکن است با نمونه های کوچک قدرت کمی داشته باشد و حتی برای اختلاف های کوچک در نمونه های بزرگ نتایج آماری معنی دار بدهد.
- فرض استقلال: این آزمون فرض می کند که داده های مقایسه شده مستقل هستند و برای داده های وابسته مناسب نیست.
- محدود به داده های پیوسته: آزمون KS برای داده های پیوسته طراحی شده و برای داده های گسسته یا ترتیبی نیاز به اصلاح دارد.
- حساسیت محدود به ویژگی های خاص توزیعی: این آزمون تفاوت های عمومی بین توزیع ها را بررسی می کند و ممکن است نسبت به ویژگی های خاص توزیعی حساس نباشد.
- احتمال خطای نوع اول در مقایسه های متعدد: استفاده از چند آزمون KS یا استفاده از آن در چارچوب بزرگتر آزمون فرض ممکن است احتمال خطای نوع اول را افزایش دهد.
نتیجه گیری
آزمون کولموگروف اسمیرنوف یک ابزار آماری قدرتمند برای سنجش تطابق داده ها با توزیع نظری و مقایسه دو نمونه مستقل است. این آزمون مزایای بسیاری از جمله عدم نیاز به فرضیات پارامتریک، قابلیت استفاده در نمونه های کوچک و بزرگ و انعطاف پذیری در تحلیل داده های یک بعدی و چندبعدی دارد. با این حال، محدودیت هایی مانند حساسیت به اندازه نمونه، نیاز به استقلال داده ها و محدودیت در داده های گسسته نیز وجود دارد. با درک صحیح کاربردها، نحوه محاسبه آماره آزمون و تفسیر نتایج، پژوهشگران و تحلیلگران می توانند از آزمون کولموگروف اسمیرنوف برای تحلیل دقیق داده ها، بررسی فرضیات توزیعی و تصمیم گیری آماری مطمئن استفاده کنند و ارزش علمی و عملی پروژه های خود را افزایش دهند. اگرچه معیارهای مبتنی بر نظریه اطلاعات مانند واگرایی JS، PSI و KL انعطاف بیشتری در انواع ویژگی ها دارند، آزمون کولموگروف اسمیرنف همچنان برای بسیاری از کاربردها، به ویژه در یادگیری ماشین، مناسب است.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











