آنالیز واریانس یک طرفه: فرمول، محاسبه و پیاده سازی در SPSS

- آزمون تحلیل واریانس یک طرفه (One-Way ANOVA)
- کاربردهای رایج آنالیز واریانس یک طرفه
- الزامات داده ها در تحلیل واریانس یک طرفه
- نکات عملی آنالیز واریانس یک طرفه
- فرضیه ها در آنالیز واریانس یک طرفه
- آماره آزمون واریانس یک طرفه
- تنظیم داده ها در آنالیز واریانس یک طرفه
- اجرای آزمون تحلیل واریانس یک طرفه در SPSS
- مثال برای اجرای ANOVA یک طرفه
چکیده مقاله:
آنالیز واریانس یک طرفه (One-Way ANOVA) یکی از روش های آماری پرکاربرد است که برای مقایسه میانگین ها در بیش از دو گروه استفاده می شود. این روش به پژوهشگران کمک می کند تا دریابند آیا تفاوت معنی داری بین گروه ها وجود دارد یا خیر. در واقع، آنالیز واریانس یک طرفه بررسی می کند که آیا متغیر مستقل، تأثیر معنی داری بر متغیر وابسته دارد یا نه. به عنوان مثال، اگر بخواهیم اثر نوع رژیم غذایی را بر وزن افراد بررسی کنیم، می توانیم از این روش استفاده نماییم. این تحلیل بر اساس مقایسه واریانس های بین گروهی و درون گروهی استوار است.
مزیت اصلی آنالیز واریانس یک طرفه در مقایسه با آزمون t دو نمونه ای این است که می تواند به طور همزمان بیش از دو گروه را مقایسه کند. این ویژگی به ویژه در تحقیقات علمی که شامل چندین متغیر یا شرایط مختلف هستند، بسیار مفید است. با این حال، برای استفاده صحیح از این روش، باید پیش فرض هایی مانند نرمال بودن داده ها، همگنی واریانس ها و استقلال مشاهدات رعایت شوند. عدم رعایت این پیش فرض ها می تواند منجر به نتایج نادرست گردد.
آزمون تحلیل واریانس یک طرفه (One-Way ANOVA)
تحلیل واریانس یک طرفه، که به اختصار One-Way ANOVA نیز نامیده می شود، میانگین های دو یا چند گروه مستقل را مقایسه می کند تا مشخص شود آیا شواهد آماری وجود دارد که نشان دهد میانگین های مرتبط با جامعه آماری به طور معناداری با یکدیگر تفاوت دارند یا خیر. این آزمون یک آزمون پارامتریک است.
این آزمون با نام های زیر نیز شناخته می شود:
- تحلیل واریانس یک عاملی
- تحلیل واریانس یک طرفه
- تحلیل واریانس بین گروهی
متغیرهای استفاده شده در این آزمون عبارتند از:
- متغیر وابسته
- متغیر مستقل: این متغیر، که به عنوان متغیر گروهبندی یا عامل نیز شناخته می شود، موارد را به دو یا چند سطح یا گروه مجزا تقسیم می کند.
کاربردهای رایج آنالیز واریانس یک طرفه
آنالیز واریانس یک طرفه معمولاً برای تحلیل داده های مربوط به مطالعات زیر استفاده می شود:
- مطالعات میدانی
- آزمایش ها
- شبه آزمایش ها
این آزمون اغلب برای بررسی موارد زیر به کار می رود:
- تفاوت های آماری میان میانگین های دو یا چند گروه
- تفاوت های آماری میان میانگین های دو یا چند مداخله
- تفاوت های آماری میان میانگین های دو یا چند امتیاز تغییر
توجه: هرچند آزمون تحلیل واریانس یک طرفه و آزمون t مستقل می توانند میانگین های دو گروه را مقایسه کنند، اما تنها آزمون تحلیل واریانس یک طرفه قادر است میانگین های سه یا چند گروه را مقایسه کند.
توجه: اگر متغیر گروه بندی فقط شامل دو گروه باشد، نتایج آزمون تحلیل واریانس یکطرفه و آزمون t مستقل معادل خواهند بود. در واقع، اگر هر دو آزمون t مستقل و آنالیز واریانس یک طرفه را در این شرایط اجرا کنید، می توانید تأیید کنید که t² = F.
الزامات داده ها در تحلیل واریانس یک طرفه
داده های شما باید شرایط زیر را داشته باشند:
- متغیر وابسته پیوسته (در سطح فاصله ای یا نسبی)
- متغیر مستقل دسته ای (شامل دو یا چند گروه)
- موارد مستقل/گروه های مستقل:
- بین افراد هر گروه رابطه ای وجود نداشته باشد.
- هیچ فردی نمی تواند همزمان در دو گروه باشد.
- افراد یک گروه نمی توانند بر افراد گروه دیگر تأثیر بگذارند.
- نمونه تصادفی از جامعه آماری
- توزیع نرمال (تقریباً) متغیر وابسته برای هر گروه
- توزیع های غیرنرمال، به ویژه آن هایی که دارای دنباله های پهن یا به شدت چوله هستند، توان آزمون را به طور قابل توجهی کاهش می دهند.
- در نمونه های متوسط یا بزرگ، نقض نرمال بودن ممکن است به مقادیر p نسبتاً دقیقی منجر شود.
- همگنی واریانس ها (واریانس ها باید تقریباً در بین گروه ها برابر باشند):
- در صورتی که این فرض نقض شود و اندازه نمونه ها در گروه ها متفاوت باشد، مقدار p آزمون F کلی قابل اعتماد نیست. در این شرایط باید از آمار جایگزین مانند آمار Browne-Forsythe یا Welch استفاده شود.
- اگر این فرض نقض شود، حتی در صورتی که اندازه نمونه ها در گروه ها تقریباً برابر باشند، نتایج آزمون های پس از hoc ممکن است قابل اعتماد نباشند.
- عدم وجود داده های پرت
توجه: زمانی که فرض های نرمال بودن، همگنی واریانس ها، یا عدم وجود داده های پرت برای تحلیل واریانس یکطرفه رعایت نشود، می توانید از آزمون ناپارامتری Kruskal-Wallis استفاده کنید.
نکات عملی آنالیز واریانس یک طرفه
پژوهشگران معمولاً از قوانین زیر برای تحلیل واریانس یک طرفه استفاده می کنند:
- هر گروه باید حداقل شامل 6 نفر باشد (ترجیحاً بیشتر؛ استنباط درباره جامعه آماری با تعداد کم دشوارتر خواهد بود).
- طراحی های متعادل (یعنی تعداد برابر افراد در هر گروه) ایدهآل هستند؛ طراحی های بسیار نامتعادل می توانند احتمال نقض الزامات/فرضیات را افزایش دهند و اعتبار آزمون F را تحت تأثیر قرار دهند.
فرضیه ها در آنالیز واریانس یک طرفه
فرضیه های صفر و جایگزین در آزمون تحلیل واریانس یکطرفه به صورت زیر بیان می شوند:
- فرضیه صفر (H0):
µ1 = µ2 = µ3 = … = µk (تمام میانگین های جامعه برابر هستند) - فرضیه جایگزین (H1):
حداقل یک µi متفاوت است (حداقل یکی از میانگین های جامعه با دیگران برابر نیست).
که در اینجا:
- µi میانگین جامعه برای گروه iام است (i = 1, 2, …, k).
توجه: آزمون تحلیل واریانس یک طرفه به عنوان یک آزمون “کلی” (omnibus، به معنی “همه” در لاتین) در نظر گرفته می شود، زیرا آزمون F نشان می دهد که آیا مدل به طور کلی معنادار است یا خیر، یعنی آیا تفاوت معناداری در میانگین های گروه ها وجود دارد یا خیر. با این حال، این آزمون مشخص نمی کند کدام میانگین متفاوت است. برای تعیین اینکه کدام جفت میانگین ها تفاوت معناداری دارند، به آزمون های مقایسه خاص (contrasts) یا آزمون های پس از hoc نیاز است.
آماره آزمون واریانس یک طرفه
آماره آنالیز واریانس یک طرفه با F نشان داده می شود. برای یک متغیر مستقل با k گروه، آماره F بررسی می کند که آیا میانگین های گروه ها به طور معناداری متفاوت هستند یا خیر. به دلیل پیچیدگی محاسبه آماره F نسبت به آزمون های t زوجی یا مستقل، معمولاً تمام اجزای آماره F در جدولی مشابه زیر نمایش داده می شوند:
| F | میانگین مربعات (Mean Square) | درجه آزادی (df) | مجموع مربعات (Sum of Squares) | |
|---|---|---|---|---|
| MSR/MSE | MSR | dfr | SSR | درمان (Treatment) |
| MSE | dfe | SSE | خطا (Error) | |
| dfT | SST | کل (Total) |
تعاریف:
- SSR: مجموع مربعات رگرسیون (Sum of Squares for Regression)
- SSE: مجموع مربعات خطا (Sum of Squares for Error)
- SST: مجموع مربعات کل (SST = SSR + SSE)
- dfr: درجه آزادی مدل (dfr = k – 1)
- dfe: درجه آزادی خطا (dfe = n – k)
- k: تعداد کل گروه ها (سطوح متغیر مستقل)
- n: تعداد کل مشاهدات معتبر
- dfT: درجه آزادی کل (dfT = dfr + dfe = n – 1)
- MSR: میانگین مربعات رگرسیون (MSR = SSR/dfr)
- MSE: میانگین مربعات خطا (MSE = SSE/dfe)
آماره F به صورت زیر محاسبه می شود:
F = MSR/MSE
توجه: در برخی منابع، ممکن است از نمادهای df1 یا ν1 برای درجه آزادی رگرسیون و df2 یا ν2 برای درجه آزادی خطا استفاده شود. این نمادها از حرف یونانی ν (نو) برای درجه آزادی استفاده می کنند.
برخی منابع به جای SSR (R = “رگرسیون”) از SSTr (Tr = “درمان”) و به جای SST از SSTo (To = “کل”) استفاده می کنند.
واژه های “درمان” (Treatment) یا “مدل” (Model) در علوم طبیعی و طراحی آزمایش های سنتی بیشتر رایج هستند. در علوم اجتماعی، واژه های “بین گروه ها” (Between Groups) به جای “درمان” و “درون گروه ها” (Within Groups) به جای “خطا” رایج تر هستند. نرم افزار SPSS نیز از این اصطلاحات در روش تحلیل واریانس یکطرفه استفاده می کند.
تنظیم داده ها در آنالیز واریانس یک طرفه
داده های شما باید حداقل شامل دو متغیر (ستون) باشد که در تحلیل استفاده خواهند شد:
- متغیر مستقل که باید دسته ای (اسمی یا ترتیبی) باشد و حداقل شامل دو گروه باشد.
- متغیر وابسته که باید پیوسته (سطح فاصله ای یا نسبی) باشد.
هر ردیف از مجموعه داده باید نمایانگر یک فرد یا واحد آزمایشی منحصر به فرد باشد.
توجه: روش تحلیل واریانس یکطرفه در نرم افزار SPSS نمی تواند از متغیرهای نوع رشته ای (String یا Character) استفاده کند. این متغیرها در لیست متغیرها ظاهر نمی شوند.
اگر متغیر دسته ای/عاملی شما به صورت رشته ای/کاراکتری باشد، باید آن را به متغیر عددی کدگذاری شده تبدیل کنید. خوشبختانه، روش “کدگذاری خودکار” (Automatic Recode) این تبدیل را به راحتی انجام می دهد.
اجرای آزمون تحلیل واریانس یک طرفه در SPSS
این مراحل به روش اختصاصی آزمون ANOVA یک طرفه در SPSS اشاره دارند. با این حال، چون آنالیز واریانس یک طرفه بخشی از خانواده مدل های خطی عمومی (GLM) است، میتوان این تحلیل را از طریق روش GLM تک متغیری نیز اجرا کرد. این روش دوم زمانی مفید است که تحلیل شما فراتر از ANOVA ساده بوده و شامل چندین متغیر مستقل، عوامل ثابت و تصادفی، و/یا متغیرهای وزنی و هم پراکنشی (مانند ANCOVA یک طرفه) باشد. در اینجا روش اجرای ANOVA یک طرفه با استفاده از روش اختصاصی SPSS توضیح داده میشود.
مراحل اجرای آزمون تحلیل واریانس یکطرفه در SPSS
برای اجرای آزمون تحلیل واریانس یکطرفه در SPSS، به مسیر زیر بروید:
Analyze > Compare Means > One-Way ANOVA

با این کار، پنجره آزمون ANOVA یک طرفه باز میشود. در اینجا متغیرهایی که در تحلیل استفاده میشوند را مشخص میکنید. تمام متغیرهای موجود در مجموعه داده در لیست سمت چپ نمایش داده میشوند. برای انتقال متغیرها به ناحیه مناسب، آنها را انتخاب کرده و روی دکمه فلش آبی کلیک کنید. متغیرها را میتوان به یکی از دو قسمت زیر منتقل کرد:
- Dependent List (لیست وابسته): متغیر وابسته که میانگین آنها بین گروهها مقایسه میشود. میتوانید همزمان چندین متغیر وابسته را برای مقایسه میانگینها انتخاب کنید.
- Factor (عامل): متغیر مستقل. دستهها (یا گروههای) متغیر مستقل تعیین میکنند که کدام نمونهها مقایسه شوند. متغیر مستقل باید حداقل دو دسته (گروه) داشته باشد، اما معمولاً در آنالیز واریانس یک طرفه شامل سه یا تعداد بیشتری گروه است.
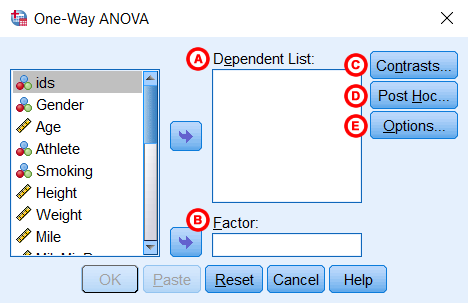
گزینه های پیشرفته در پنجره ANOVA
- Contrasts (اختیاری): در صورت نیاز، مقایسه های برنامه ریزی شده (Contrasts) را مشخص کنید که پس از آزمون کلی ANOVA انجام شوند. این مقایسه ها معمولاً برای آزمون فرضیه های خاص پیش از تحلیل دادهها (a priori) استفاده میشوند.
- Post Hoc (اختیاری): درخواست آزمون های پس از hoc (یا مقایسه های چندگانه) برای تعیین تفاوتهای معنادار میانگینها در صورت نبود فرضیه خاص. این آزمون ها هر جفت میانگین را مقایسه کرده و تصحیح های لازم را برای جلوگیری از خطای نوع اول انجام می دهند.
- Options: مشخص کردن آماره هایی که در خروجی نشان داده شوند (مانند آمار توصیفی، آزمون همگنی واریانس، Brown-Forsythe، Welch)، رسم نمودار میانگین ها و تعیین نحوه مدیریت داده های گمشده.

مقایسه های برنامه ریزی شده (Contrasts)
(اختیاری) در صورت نیاز، می توانید مقایسه های برنامه ریزی شده (Contrasts) را پس از آزمون کلی ANOVA مشخص کنید.

پنجره Contrasts در ANOVA یک طرفه
هنگامی که آزمون اولیه F نشان دهد تفاوت های معناداری بین میانگین گروه ها وجود دارد، مقایسه های برنامه ریزی شده برای تعیین اینکه کدام میانگین ها به طور خاص معنادار هستند مفید می باشند. این مقایسه ها زمانی استفاده می شوند که فرضیه های خاصی دارید که قصد دارید آن ها را آزمایش کنید.
مقایسه های برنامه ریزی شده پیش از تحلیل داده ها تصمیم گیری می شوند (a priori). این مقایسه ها واریانس را به اجزای مختلف تقسیم می کنند. این اجزاء ممکن است شامل استفاده از وزن ها، مقایسه های غیر عمودی (non-orthogonal)، مقایسه های استاندارد، و مقایسه های چند جمله ای (تحلیل روند) باشند.
منابع آنلاین و چاپی بسیاری وجود دارند که تفاوت های میان این گزینه ها را به تفصیل شرح می دهند و به کاربران کمک می کنند مقایسه های مناسب را انتخاب نمایند. برای اطلاعات بیشتر درباره مقایسه های برنامه ریزی شده، می توانید از منوی Help در SPSS استفاده کرده و راهنمای IBM SPSS را باز کنید. این گزینه در پایین پنجره ANOVA یک طرفه موجود است.
آزمون های Post Hoc
(اختیاری) می توانید درخواست آزمون های پس از hoc یا مقایسه های چندگانه را برای تعیین تفاوت های معنادار بین میانگین ها در صورت عدم وجود فرضیه خاص انجام دهید. این آزمون ها در پنجره Post Hoc Multiple Comparisons موجود هستند.
گزینه ها در پنجره Post Hoc
- فرض برابری واریانس ها (Equal Variances Assumed): مقایسه های چندگانه ای که فرض همگنی واریانس را دارند (یعنی هر گروه واریانس برابری دارد). برای اطلاعات دقیق تر درباره روش های مقایسه خاص، می توانید از دکمه Help در این پنجره استفاده کنید.
- Test (آزمون): به طور پیش فرض، آزمون فرضیه دو طرفه انتخاب می شود. در صورت تمایل، می توانید آزمون فرضیه جهت دار یک طرفه را انتخاب کنید. این حالت زمانی استفاده می شود که بخواهید از آزمون پس از hoc Dunnett استفاده کنید. برای این کار:
- تیک گزینه Dunnett را فعال کنید.
- مشخص کنید گروه کنترلی اولین یا آخرین گروه (از نظر عددی) در متغیر گروه بندی است.
- در بخش Test، یکی از گزینه های < Control یا > Control را انتخاب کنید.
- این گزینه ها نیازمند این هستند که پیش بینی کنید میانگین گروه کنترلی بزرگ تر از (> Control) یا کوچک تر از (< Control) سایر گروه ها باشد.
- فرض عدم برابری واریانس ها (Equal Variances Not Assumed): مقایسه های چندگانه ای که فرض همگنی واریانس را ندارند. برای اطلاعات دقیق تر درباره روش های مقایسه، از دکمه Help در این پنجره استفاده کنید.
- سطح معناداری (Significance level): حد مورد نظر برای معناداری آماری را تعیین می کند. به طور پیش فرض، این مقدار 0.05 تنظیم شده است.
هنگامی که آزمون اولیه F نشان دهد تفاوت های معناداری بین میانگین گروه ها وجود دارد، آزمون های پس از hoc برای تعیین اینکه کدام میانگین ها معنادار هستند مفید می باشند. این آزمون ها هر جفت میانگین را مقایسه می کنند، اما برخلاف آزمون های t، مقدار معناداری را برای جلوگیری از خطای نوع اول تصحیح می کنند.
سایر گزینه ها
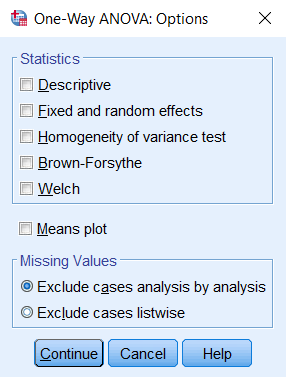
با کلیک بر روی دکمه Options، پنجره ای باز می شود که می توانید موارد زیر را مشخص کنید:
- آمارهایی که باید در خروجی نمایش داده شوند (Statistics): شامل آمارهای توصیفی، اثرات ثابت و تصادفی، آزمون همگنی واریانس، Brown-Forsythe، و Welch.
- رسم نمودار میانگین ها (Means plot): گزینه ای برای مشاهده نمودار میانگین ها.
- نحوه مدیریت داده های گمشده (Missing Values): شامل گزینه های Exclude cases analysis by analysis یا Exclude cases listwise.
پس از مشخص کردن تنظیمات، روی Continue کلیک کنید.
مثال برای اجرای ANOVA یک طرفه
بیان مسئله
در یک مجموعه داده نمونه، متغیر Sprint زمان دویدن پاسخ دهنده (بر حسب ثانیه) برای یک فاصله مشخص است و متغیر Smoking نشان دهنده وضعیت سیگار کشیدن پاسخ دهنده است (0 = غیرسیگاری، 1 = سیگاری سابق، 2 = سیگاری فعلی). هدف، آزمون این است که آیا تفاوت معناداری در زمان دویدن با توجه به وضعیت سیگار کشیدن وجود دارد یا خیر. زمان دویدن به عنوان متغیر وابسته و وضعیت سیگار کشیدن به عنوان متغیر مستقل عمل می کند.
توصیف اولیه داده ها
پیش از انجام آزمون ANOVA، باید آمار توصیفی و نمودارها را بررسی کنیم:
- زمان های دویدن متغیری پیوسته با محدوده ای از 4.5 تا 9.6 ثانیه هستند و میانگین 6.6 ثانیه دارند (n = 374).
- میانگین ها با توجه به وضعیت سیگار کشیدن به صورت زیر است:
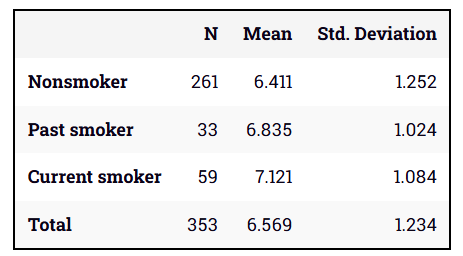

توزیع داده ها با توجه به گروه ها
اجرای تحلیل
- روی مسیر Analyze > Compare Means > One-Way ANOVA کلیک کنید.
- متغیر Sprint را به کادر Dependent List و متغیر Smoking را به کادر Factor منتقل کنید.
- در Options، گزینه Means plot را انتخاب کرده و Continue را بزنید.
- OK را کلیک کنید.
کد SPSS (Syntax)
نتایج آزمون
جدول ANOVA خروجی به صورت زیر است:

نمودار میانگین ها نیز به وضوح نشان می دهد که سیگاری های فعلی کندترین زمان دویدن و غیرسیگاری ها سریع ترین زمان دویدن را دارند.
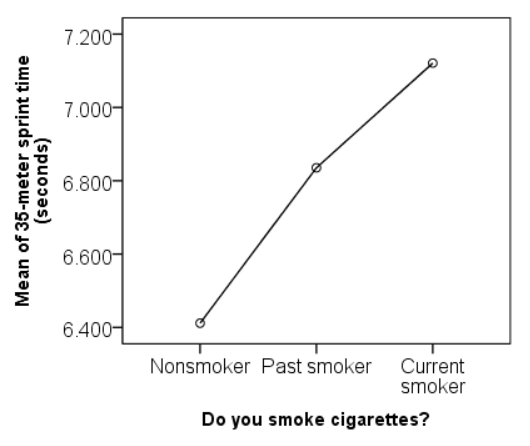
بحث و نتیجه گیری
می توان نتیجه گرفت که میانگین زمان دویدن برای حداقل یکی از گروه های سیگار کشیدن به طور معناداری متفاوت است (F(2, 350) = 9.209، p < 0.001). با این حال، ANOVA مشخص نمیکند کدام میانگین ها متفاوت هستند. برای تعیین این مورد، نیاز به انجام آزمون های مقایسه ای پس از hoc داریم.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]












با سلام
خیلی عالی توضیح دادین. برای من که با دیتا سرو کار دارم دیدگاهی عالی فراهم کردین. به دور از استفاده از کلمات قلمبه سلمبه که فقط ترجمه تحت الفظی بعضی کلمات انگلیسی است و در غالب متون استفاده می شوند، خیلی قابل فهم توضیح داده شده است. ممنون از شما
سلام وقت بخیر
خوش حالیم که مفید واقع شده بازهم اگر سوالی بود در خدمت هستیم.