روش همبستگی اسپیرمن (Spearman Correlation)

چکیده مقاله:
ضریب همبستگی اسپیرمن یکی از روش های آماری غیرپارامتری برای سنجش ارتباط بین دو متغیر است. این روش زمانی کاربرد دارد که داده ها از نوع رتبه ای باشند یا زمانی که فرض نرمال بودن داده ها برقرار نباشد. اسپیرمن به جای مقادیر واقعی داده ها، رتبه آن ها را در نظر می گیرد و میزان هماهنگی بین رتبه ها را محاسبه می کند. به بیان دیگر، اگر با افزایش یک متغیر، مقدار متغیر دیگر نیز به طور منظم افزایش یا کاهش یابد، همبستگی اسپیرمن مقدار بالایی را نشان خواهد داد.
ویژگی مهم این روش آن است که نسبت به داده های پرت و توزیع غیرنرمال حساسیت کمی دارد، به همین دلیل در بسیاری از پژوهش های علوم انسانی، علوم اجتماعی و علوم رفتاری استفاده می شود. مقدار ضریب همبستگی اسپیرمن بین منفی یک تا مثبت یک قرار دارد؛ مقادیر نزدیک به مثبت یک نشان دهنده ارتباط مستقیم قوی، مقادیر نزدیک به منفی یک بیانگر ارتباط معکوس قوی و مقادیر نزدیک به صفر نشان دهنده نبود ارتباط رتبه ای بین دو متغیر می باشد. این روش ابزاری مناسب برای تحلیل روابط غیرخطی و بررسی الگوهای کلی بین متغیرها محسوب می شود.
روش همبستگی اسپیرمن (Spearman Correlation) یکی از قدرتمند ترین ابزار های آماری برای سنجش میزان و جهت ارتباط بین دو متغیر رتبه ای است که در حوزه های مختلف پژوهشی، از علوم اجتماعی گرفته تا تحلیل داده های علمی، کاربرد فراوان دارد. برخلاف روش های همبستگی خطی که تنها روابط مستقیم و متناسب را بررسی می کنند، این روش قادر است حتی در شرایطی که رابطه میان داده ها غیرخطی اما یکنوا باشد، تصویر دقیقی از میزان همبستگی ارائه دهد. ماهیت این روش بر پایه رتبه بندی داده ها و سنجش روند تغییرات آن ها بنا شده است و به همین دلیل در موقعیت هایی که مقیاس اندازه گیری داده ها نسبی یا ترتیبی است، عملکردی بسیار قابل اعتماد دارد. استفاده صحیح از روش همبستگی اسپیرمن (Spearman Correlation) به پژوهشگر کمک می کند تا نه تنها وجود یا عدم وجود ارتباط بین دو متغیر را مشخص کند، بلکه جهت این ارتباط را نیز به دقت تحلیل نماید. در این آموزش همراه ما باشید تا این روش را برای شما به طور کامل با شرح مثال توضیح دهیم.
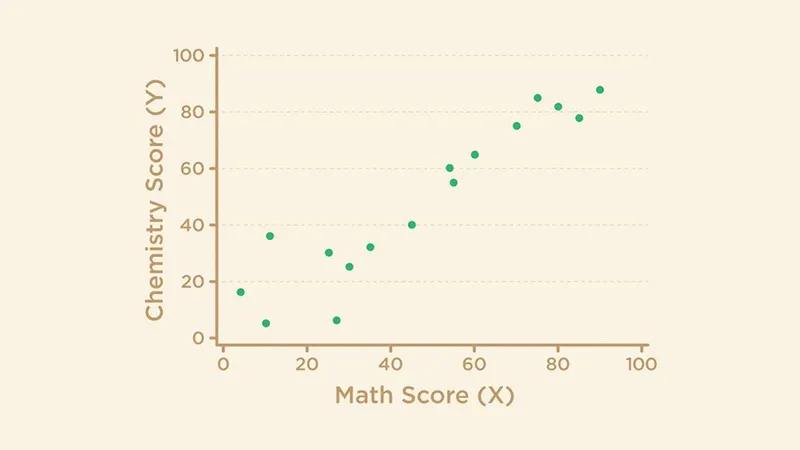
تابع یکنوا (Monotonic Function) چیست؟
برای درک بهتر روش همبستگی اسپیرمن (Spearman Correlation)، لازم است ابتدا با مفهوم تابع یکنوا آشنا شویم. تابع یکنوا به تابعی گفته می شود که با تغییر متغیر مستقل آن، مقدار تابع یا همواره افزایش می یابد یا همواره کاهش پیدا می کند، بدون آنکه جهت تغییراتش برعکس شود.
به عبارت دیگر، در یک تابع یکنوا، روند تغییرات یا همیشه صعودی است یا همیشه نزولی و هیچ نقطه ای وجود ندارد که روند از افزایش به کاهش یا بالعکس تغییر کند. این ویژگی باعث می شود چنین توابعی در تحلیل آماری و به ویژه در محاسبه روش همبستگی اسپیرمن (Spearman Correlation) کاربرد بالایی داشته باشند، زیرا این روش به جای بررسی روابط خطی، بر اساس روابط یکنوا یا غیرخطی ولی ثابت روند عمل می کند.
نمودار زیر نمونه ای از یک تابع یکنوا را نشان می دهد:
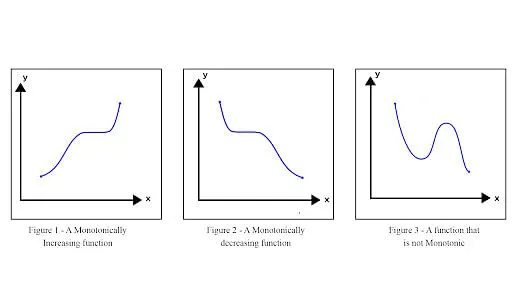
نمودار تابع یکنوا
انواع توابع یکنوا
- افزایشی یکنوا :(Monotonically Increasing) زمانی که متغیر X افزایش پیدا می کند، متغیر Y هرگز کاهش نمی یابد. در این حالت رابطه میان دو متغیر همواره صعودی است.
- کاهشی یکنوا: (Monotonically Decreasing) زمانی که متغیر X افزایش پیدا می کند، متغیر Y هرگز افزایش نمی یابد. در این حالت رابطه میان دو متغیر همواره نزولی است.
- غیر یکنوا: (Not Monotonic) زمانی که متغیر X افزایش پیدا می کند، متغیر Y گاهی کاهش و گاهی افزایش می یابد. در این شرایط، روند تغییرات دو متغیر ثابت نبوده و همسو عمل نمی کنند.
روش همبستگی اسپیرمن (Spearman Correlation)
روش همبستگی اسپیرمن (Spearman Correlation) معیاری برای سنجش میزان و جهت ارتباط بین دو متغیر رتبه ای است. این روش در اصل نشان می دهد که تا چه اندازه رابطه بین دو متغیر را می توان با استفاده از یک تابع یکنوا توصیف کرد. به عبارت دیگر، اگر دو متغیر دارای رابطه ای باشند که روند آن همواره صعودی یا همواره نزولی است، روش همبستگی اسپیرمن می تواند قدرت و جهت این رابطه را به طور دقیق مشخص کند.
فرمول ضریب همبستگی رتبه ای اسپیرمن به صورت زیر بیان می شود:
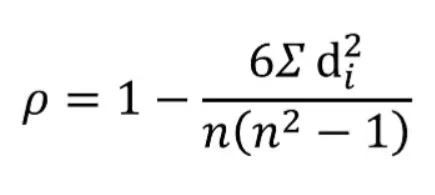
فرمول ضریب همبستگی رتبه ای اسپیرمن
نمادها و مقادیر در فرمول
در فرمول ضریب همبستگی رتبه ای اسپیرمن:
- ρ نشان دهنده ضریب همبستگی رتبه ای اسپیرمن (Spearman’s rank correlation coefficient) است.
- di بیانگر اختلاف بین دو رتبه هر مشاهده می باشد.
- n تعداد کل مشاهدات را نشان می دهد.
دامنه مقادیر ضریب همبستگی اسپیرمن
مقدار ضریب روش همبستگی اسپیرمن (Spearman Correlation) عددی بین 1+ تا 1- است که هر کدام از این مقادیر معنای خاص خود را دارند:
- مقدار 1 + نشان دهنده یک ارتباط کامل و مثبت بین رتبه ها است، یعنی هر چه رتبه یک متغیر افزایش پیدا کند، رتبه متغیر دیگر نیز به همان نسبت افزایش می یابد.
- مقدار 0 به این معنا است که هیچ ارتباط معنا داری بین رتبه ها وجود ندارد.
- مقدار 1 – نشان دهنده یک ارتباط کامل و منفی بین رتبه ها است، یعنی با افزایش رتبه یک متغیر، رتبه متغیر دیگر کاهش می یابد.
برای درک بهتر عملکرد روش همبستگی اسپیرمن (Spearman Correlation)، بهتر است یک مثال ساده بررسی کنیم تا روند محاسبه و تفسیر نتایج آن روشن تر شود.
مثال روش همبستگی اسپیرمن (Spearman Correlation)
فرض کنید نمرات ۵ دانش آموز در دو درس ریاضی و علوم در اختیار داریم که به صورت جدول زیر ثبت شده اند.
نمرات ۵ دانش آموز در دو درس ریاضی و علوم
| دانش آموزان | درس ریاضی | درس علوم |
| A | 35 | 24 |
| B | 20 | 35 |
| C | 49 | 39 |
| D | 44 | 48 |
| E | 30 | 45 |
گام اول: یک جدول برای داده های موجود ایجاد می کنیم تا نمرات هر دانش آموز در هر درس مشخص شود.
گام دوم: به هر یک از داده ها رتبه اختصاص می دهیم. این رتبه بندی باید به صورت نزولی انجام شود، یعنی بیشترین نمره رتبه ۱ و کمترین نمره رتبه ۵ را دریافت می کند.
گام سوم: اختلاف بین رتبه های هر دانش آموز در دو درس را محاسبه می کنیم و آن را با نماد d نمایش می دهیم. سپس مقدار d به توان ۲ را برای هر مشاهده به دست می آوریم.
گام چهارم: مجموع مقادیر به توان ۲ (Σd²) را محاسبه می کنیم. در این مثال، مجموع به توان ۲ برابر با ۱۴ به دست آمده است.
| دانش آموزان | ریاضی | رتبه | علوم | رتبه | d | مربع d |
| A | 35 | 3 | 24 | 5 | 2 | 4 |
| B | 20 | 5 | 35 | 4 | 1 | 1 |
| C | 49 | 1 | 39 | 3 | 2 | 4 |
| D | 44 | 2 | 48 | 1 | 1 | 1 |
| E | 30 | 4 | 45 | 2 | 2 | 4 |
| 14 |
گام پنجم: مقادیر به دست آمده را در فرمول روش همبستگی اسپیرمن (Spearman Correlation) قرار می دهیم:
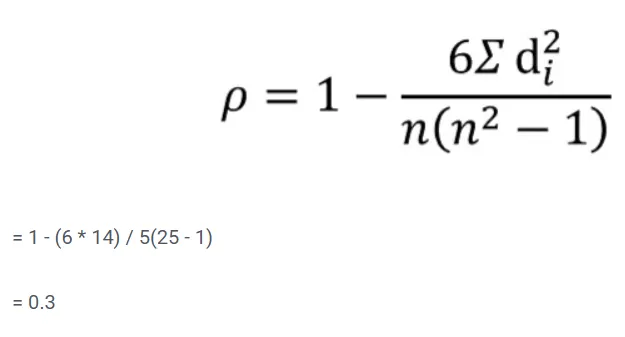
قرار دادن مقادیر به دست آمده در فرمول روش همبستگی اسپیرمن (Spearman Correlation)
بنابراین، ضریب همبستگی رتبه ای اسپیرمن برای این داده ها برابر با 0.3 است. از آنجا که این مقدار به عدد صفر نزدیک است، نتیجه می گیریم که بین رتبه های دو درس ریاضی و علوم، ارتباط ضعیفی وجود دارد.
این مثال نشان می دهد که روش همبستگی اسپیرمن (Spearman Correlation) تنها زمانی مقادیر بالا (نزدیک به ۱ یا -۱) به دست می آورد که تغییرات رتبه ها به شکل یکنوا و منظم باشد، در غیر این صورت مقدار به صفر نزدیک می شود.
جمع بندی
در مجموع، روش همبستگی اسپیرمن (Spearman Correlation) یک انتخاب ایده آل برای سنجش روابط یکنوا میان متغیرها، به ویژه زمانی که داده ها از نوع رتبه ای یا غیرخطی باشند، محسوب می شود. این روش با استفاده از رتبه بندی و محاسبه ضریب همبستگی، تصویر روشنی از قدرت و جهت رابطه بین متغیرها ارائه می دهد و می تواند در تحلیل های علمی، تحقیقاتی و حتی تجزیه و تحلیل های بازار، نقشی کلیدی ایفا کند. آگاهی از نحوه محاسبه، تفسیر مقادیر به دست آمده و شناخت شرایط مناسب برای استفاده از این روش، باعث می شود پژوهشگر یا تحلیلگر بتواند تصمیمات دقیق تر و مبتنی بر داده بگیرد. بنابراین، بهره گیری هوشمندانه از روش همبستگی اسپیرمن (Spearman Correlation) نه تنها به درک بهتر الگوهای موجود در داده ها کمک می کند، بلکه مسیر تحقیقات و تحلیل های آماری را نیز به شکلی اصولی و هدفمند هدایت می نماید.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











