آزمون تی (T-test) – معنی، انواع، مثال ها، فرمول، محاسبه

چکیده مقاله :
یکی دیگر از آزمون های معروف در تحلیل اماری آزمون تی یا همان t-test می باشد. به طور خلاصه این تحلیل به بررسی میانگین دو نمونه می پردازد. در این مقاله به طور جامع و کامل شما را با معنی و مفهوم آزمون تی آشنا می کنیم. انواع آن را با ارائه فرمول هریک معرفی میکنیم. توضیح میدهیم که چه موقع شما جایز به استفاده از این تحلیل هستید و چه مفروضاتی بر آن حاکم است. به سوالات پر تکرار شما پاسخ داده و مثال هایی ذکر کرده و آن ها را حل می کنیم.
1- مفهوم و تحلیل آزمون T
آزمون T آخرین معیار آماری برای تعیین تفاوت بین دو میانگین است که ممکن است مرتبط باشند یا نباشند. این آزمایش از نمونههای انتخابی تصادفی از دو دسته یا گروه استفاده میکند. این یک روش آماری است که در آن نمونه ها به صورت تصادفی انتخاب می شوند و توزیع نرمال کاملی وجود ندارد.
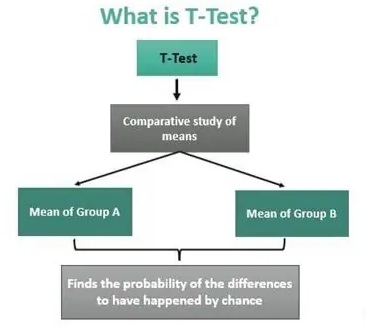
آزمون تی چیست ؟
با توجه به اینکه آیا نمونههای مورد تجزیه و تحلیل از یک دسته هستند یا دستههای مجزا نوع آزمون T که باید انجام شود تعیین میشود. استنتاج بهدستآمده در این فرآیند، احتمال وقوع اختلاف میانگینها را به طور تصادفی نشان میدهد. این آزمون هنگام مقایسه سن جمعیت، طول محصول از دو گونه مختلف، نمرات دانشآموز و غیره مفید است.
جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تحلیل آماری چیست مطالعه نمایید.
به طور کلی :
• آزمون T روشی آماری برای مقایسه میانگین یا نسبت دو نمونه جمع آوری شده از یک گروه یا دسته های مختلف است.
• هدف آن آزمون فرضیه است که برای آزمایش یک فرضیه مربوط به یک جمعیت معین استفاده می شود.
• تفاوت بین میانگین جمعیت و مقدار فرضی است.
• واریانس تک نمونه ای، دو نمونه ای، زوجی، مساوی و نابرابر انواع تست های تی هستند که کاربران می توانند برای مقایسه میانگین ها استفاده کنند.
1-1- تحلیل و توضیح آزمون تی
آزمون T مجموعه ای از داده های جمع آوری شده از دو گروه مشابه یا متفاوت را مطالعه می کند تا احتمال تفاوت در نتیجه را نسبت به آنچه که معمولاً به دست می آید، تعیین کند. دقت آزمایش به عوامل مختلفی از جمله الگوهای توزیع مورد استفاده و انواع تأثیرگذار بر نمونه های جمع آوری شده بستگی دارد. بسته به پارامترها، آزمون انجام می شود و یک مقدار T به عنوان استنتاج آماری احتمال اینکه نتیجه معمول به طور تصادفی هدایت می شود، به دست می آید.
به عنوان مثال، اگر کسی بخواهد بفهمد که آیا میانگین طول گلبرگ های یک گل متعلق به دو گونه مختلف یکسان است، می توان آزمون T انجام داد. کاربر می تواند گلبرگ ها را به طور تصادفی از دو گونه دیگر از آن گل انتخاب کند و به یک نتیجه استاندارد برسد. تفسیر نهایی آزمون T را می توان به یکی از دو روش زیر بدست آورد:
• فرضیه صفر نشان می دهد که تفاوت بین میانگین ها صفر است و هر دو میانگین برابر هستند.
• یک فرضیه جایگزین دلالت بر تفاوت بین میانگین از صفر دارد. این فرضیه فرضیه صفر را رد می کند و نشان می دهد که مجموعه داده کاملاً دقیق است و تصادفی نیست.
با این حال، این آزمون T زمانی معتبر است یا به بیان دیگر باید زمانی انجام شود که میانگین تنها دو دسته یا گروه نیاز به مقایسه داشته باشد. به محض اینکه تعداد مقایسه هایی که باید انجام شود بیش از دو باشد، انجام این کار توصیه نمی شود.
2-1- مفروضات در آزمون T
آزمون تی بر اساس مجموعه ای از مفروضات اجرا می شود که به شرح زیر است:
• مقیاس اندازه گیری مورد استفاده برای آزمون چنین فرضیه هایی از مجموعه ای از الگوهای پیوسته یا ترتیبی پیروی می کند. پارامترهای محاسبه شده و متغیرهای مؤثر بر نمونه ها بر اساس در نظر گرفتن استاندارد است.
• آزمون ها کاملا بر اساس نمونه گیری تصادفی است. از آنجایی که هیچ فردیت در نمونه ها حفظ نمی شود، قابلیت اطمینان اغلب مورد سوال قرار می گیرد.
• هنگامی که داده ها با توجه به توزیع آزمون T رسم می شوند، باید از توزیع نرمال پیروی کنند و یک نمودار منحنی زنگی (bell-curved graph) ایجاد کنند.
• برای bell-curved graph واضح تر، اندازه نمونه باید بزرگتر باشد.
• واریانس باید به گونه ای باشد که انحراف معیار نمونه ها تقریباً برابر باشد.
2- انواع آزمون تی (T-test)
برخی از انواع پرکاربرد آزمون تی به شرح زیر است:
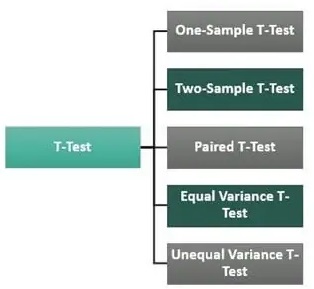
انواع آزمون تی
1-2- آزمون تی تک نمونه (One-Sample T-Test)
در حین انجام این آزمون، مین یا میانگین یک گروه با میانگین تعیین شده که یا مقدار نظری یا میانگین جامعه است، مقایسه می شود. به عنوان مثال، معلمی می خواهد میانگین قد دانش آموزان کلاس 5 را بفهمد و آن را با مقدار تعیین شده بیش از 45 کیلوگرم مقایسه کند.
معلم ابتدا به طور تصادفی گروهی از دانش آموزان را انتخاب می کند و برای رسیدن به این هدف، وزن های فردی را ثبت می کند. سپس، او میانگین وزن آن گروه را مییابد و بررسی میکند که آیا با مقدار مجموعه استاندارد 45+ مطابقت دارد یا خیر. فرمول مورد استفاده برای به دست آوردن نتایج آزمون t تک نمونه ای به شرح زیر است:
که در آن،
t-statistics = T
m = میانگین گروه
μ= ارزش میانگین نظری جمعیت
s = انحراف معیار گروه
n = حجم نمونه
2-2- آزمون تی دو نمونه ای مستقل (Independent Two-Sample T-Test)
این آزمایش زمانی انجام می شود که نمونه هایی از دو گروه، گونه یا جمعیت مختلف مورد مطالعه و مقایسه قرار می گیرند که به عنوان آزمون تی مستقل نیز شناخته می شود. برای مثال، اگر معلمی بخواهد قد دانشآموزان پسر و دختر کلاس 5 را با هم مقایسه کند، از آزمون تی دو نمونهای مستقل استفاده میکند.
فرمول T-test مورد استفاده برای محاسبه این است:
جایی که،
mA – mB = میانگین نمونهها از دو گروه یا جمعیت مختلف
nA – nB = اندازه نمونه مربوطه
s2 = انحراف معیار یا واریانس مشترک دو نمونه
3-2- تست T دو نمونه پیر (Paired Sample T-Test)
این آزمون فرضیه زمانی انجام می شود که دو گروه متعلق به یک جمعیت یا گروه باشند. گروه ها یا در دو زمان مختلف یا در دو شرایط مختلف مورد مطالعه قرار می گیرند. فرمول مورد استفاده برای بدست آوردن مقدار t به صورت زیر است:
جایی که،
t-statistics = T
m = میانگین گروه
μ = ارزش میانگین نظری جمعیت
s = انحراف معیار گروه
n = حجم نمونه
4-2- آزمون تی واریانس برابر (Equal Variance T-Test)
این آزمون زمانی انجام می شود که حجم نمونه در هر گروه یا جامعه یکسان باشد یا واریانس دو مجموعه داده مشابه باشد. به آن pooled T-test نیز نام می نهند. فرمول اعمال شده در اینجا به شرح زیر است:
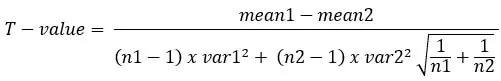
جایی که،
Mean1 و mean2 = مقدار متوسط هر مجموعه از نمونه ها
var1 و var2 = واریانس هر مجموعه از نمونه ها
n1 و n2 = تعداد رکوردها در هر مجموعه
5-2- آزمون تی واریانس نابرابر (Unequal Variance T-Test)
از آزمون واریانس نابرابر زمانی استفاده می شود که واریانس و تعداد نمونه ها در هر گروه متفاوت باشد. اغلب از آن به عنوان Welch's test یاد می شود و فرمول این است:
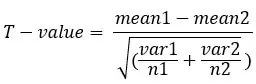
جایی که،
mean1 و mean2 = مقدار متوسط هر مجموعه از نمونه ها
var1 و var2 = واریانس هر مجموعه از نمونه ها
n1 و n2 = تعداد رکوردها در هر مجموعه
3- مثال با محاسبه
بیاید نمرات هر رشته را در آزمونی که در دو مرحله برگزار می شود در نظر بگیریم.
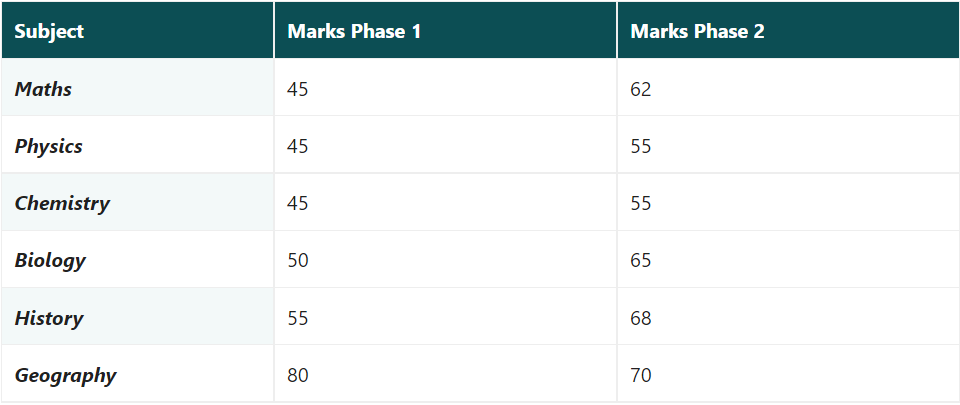
مرحله 1: امتیازهای کسب شده در هر دو مرحله را کم کنید
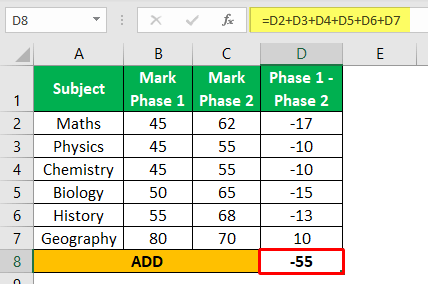
مرحله 2: تمام تفاوت ها را جمع کنید، یعنی 55-
مرحله 3: تفاوت ها را مربع کنید
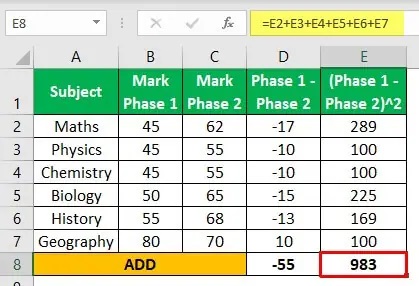
مرحله 4: تمام مربع های اختلاف را جمع کنید، یعنی 983
مرحله 5: استفاده از فرمول برای محاسبه مقدار T
![]()
= -9.16/√ / (6-1) *6
= -9.16/√15.96
= -9.16/3.99
مقدار T = -2.29
حال، درجات آزادی (degrees of freedom) را بدست آورید. برای به دست آوردن آن، 1 را از حجم نمونه کم کنید (1 – 6 = 5). مورد بعدی این است که مقدار p را پیدا کنید
، که اگر مقدار آن کوچکتر باشد، از نتیجه فرضیه صفر پشتیبانی می کند. به عنوان مثال، اگر مقدار p چیزی در حدود 0.9 باشد، یعنی 90٪، نشان می دهد که مقدار T بدست آمده احتمال مشاهده تصادفی را دارد. از طرف دیگر، اگر مقدار p حدود 0.025 باشد، یعنی 2.5٪، نتیجه یا مقدار t به دست آمده قابل توجه است.
4- سوالات پرتکرار (سؤالات متداول)
T-Test چیست؟
آزمون تی تفاوت بین دو میانگین را اندازه گیری می کند که ممکن است به یکدیگر مرتبط باشند یا نباشند، که نشان می دهد احتمال تصادفی بودن تفاوت ها وجود دارد. دقت مقادیر بهدستآمده به عوامل مختلفی از جمله الگوهای توزیع مورد استفاده و انواع تأثیرگذار بر نمونههای جمعآوریشده بستگی دارد.
چه زمانی از T-Test استفاده می شود؟
T-Test فقط زمانی معتبر است که باید میانگین دو دسته یا گروه را با هم مقایسه کرد. به محض اینکه تعداد مقایسه هایی که باید انجام شود بیش از دو باشد، انجام این آزمون توصیه نمی شود.
• یک نمونه برای یافتن میانگین یا میانگین یک گروه برای مقایسه آن با میانگین تعیین شده استفاده می شود.
• یک آزمایش دو نمونه مستقل زمانی انجام می شود که نمونه هایی از دو گروه، گونه یا جمعیت مختلف مورد مطالعه و مقایسه قرار گیرند.
• نمونه زوجی آزمون فرضیه است که زمانی انجام می شود که دو گروه به یک جمعیت یا گروه تعلق داشته باشند.
• واریانس برابر زمانی انجام می شود که حجم نمونه در هر گروه یا جمعیت یکسان باشد یا واریانس دو مجموعه داده مشابه باشد.
• واریانس نابرابر زمانی استفاده می شود که واریانس و تعداد نمونه ها در هر گروه متفاوت باشد.
T-Tests و P values چه هستند؟
در حالی که مقادیر T شانس تفاوت بین میانگین های نمونه را نشان می دهد که به طور تصادفی به دست آمده است، مقادیر p احتمال وجود اثبات کافی برای نفی نداشتن تفاوت بین میانگین دو نمونه را نشان می دهد.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]

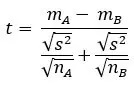
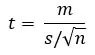











عالی بود
سلام وقت بخیر
خیلی ممنون خوش حالیم که مفید واقع شده
سلام اگر در مقایسه یک دسته داده با مقدار مرجع که باید از فرمول اول استفاده کنیم، مقدار انحراف معیار S=0 شود. در این حالت مقدار t=بینهایت می شود و t بحرانی بیشتر می شود.
در این مواقع از چه رابطه ای باید استفاده کرد؟
واریانس یعنی میزان انحراف معیار به طور مثال در مورد موضوعی که گفتید اگر مقدار انحراف معیار صفر باشه، یعنی در دو جامعه تفاوتی وجود ندارد یا دو جامعه شبیه هم هستن. اگر انحراف معیار صفر باشه مقدار t بینهایت میشه رابطه انحراف معیار و t رابطه عکس هست
سلام ممنون خیلی خوب و مختصر و مفید
سلام وقت شما بخیر
خوش حالیم که مفید واقع شده براتون دوست داشتید مطالب دیگه سایت هم دنبال کنید خوش حال میشیم
دورد وقت بخیر
ممنون از سایت خوبتون
هنگامی که واریانس دو جامعه در ازمون tبرابر نباشه از چه روشی خطای استاندارد میانگین ها رو به دست میاریم؟
سلام وقت شما بخیر
اصولا واریانس دو جامعه در آزمون تی نباید برابر باشد و اصولا برای اندازه گیری میانگین ها از آزمون همبستگی استفاده می کنیم.
با سلام
لطفا منبع این اطلاعات رو هم ذکر نمایید.
باتشکر
سلام وقت بخیر بله حتما انجام میشه
در جای حساس توضیح دادن پیچوند که کسی متوجه نشه
سلام وقت بخیر
کجا منظورتون هست اعلام کنید که بیشتر توضیح داده بشه براتون