کشیدگی در آمار چیست ؟ (Kurtosis)

چکیده مقاله :
تحلیل آماری یک حوزه بسیار گسترده و مهم می باشد که تو حل و تفسیر مسائل مهم کاربرد دارد. در تفسیر داده ها از معیارهای مختلفی استفاده می شود که یکی از آن ها کشیدگی یا kurtosis می باشد. قطعا برای شما هم سوال شده است که کشیدگی چیست و چه کاربردی در مسائل دارد. چه تفسیری می توان از آن داشت و در بحث ریسک در مسائل مالی و سهام چه تحلیلی می توان از آن داشت. نحوه محاسبه کشیدگی در اکسل و گوگل شیت به چه صورته ؟ فرمول محاسبه دستی آن چیست که در این مقاله با ذکر مثال به همه آن ها پاسخ داده شده است.

1- کشیدگی چیست ؟

کشیدگی یا Kurtosis یک معیار آماری است که برای توصیف ویژگی یک مجموعه داده استفاده می شود. هنگامی که داده های توزیع شده معمولی بر روی یک نمودار رسم می شوند، معمولاً شکل یک زنگ وارونه به خود می گیرند. به این منحنی زنگ می گویند. داده های رسم شده که از میانگین داده ها دورتر هستند معمولاً دنباله های هر طرف منحنی را تشکیل می دهند. کشیدگی یا Kurtosis نشان می دهد که چه مقدار داده در دم ها وجود دارد.

توزیع‌های با کشیدگی بزرگ، داده‌های دنباله بیشتری نسبت به داده‌های توزیع شده معمولی دارند، که به نظر می‌رسد دنباله‌ها را به سمت میانگین می‌آورد. توزیع‌های با کشیدگی کم داده‌های دم کمتری دارند، که به نظر می‌رسد دم منحنی زنگ را از میانگین دور می‌کند.

برای سرمایه گذاران، کشش بالای منحنی توزیع بازده نشان می دهد که نوسانات قیمت زیادی در گذشته (مثبت یا منفی) به دور از میانگین بازده سرمایه گذاری وجود داشته است. بنابراین، یک سرمایه گذار ممکن است با یک سرمایه گذاری با کشش بالا، نوسانات شدید قیمت را تجربه کند. این پدیده به عنوان خطر کشیدگی شناخته می شود.

 نکات کلیدی

• کورتوسیس «کشیدگی» دم‌هایی را که در توزیع‌های احتمالی یافت می‌شود، توصیف می‌کند.
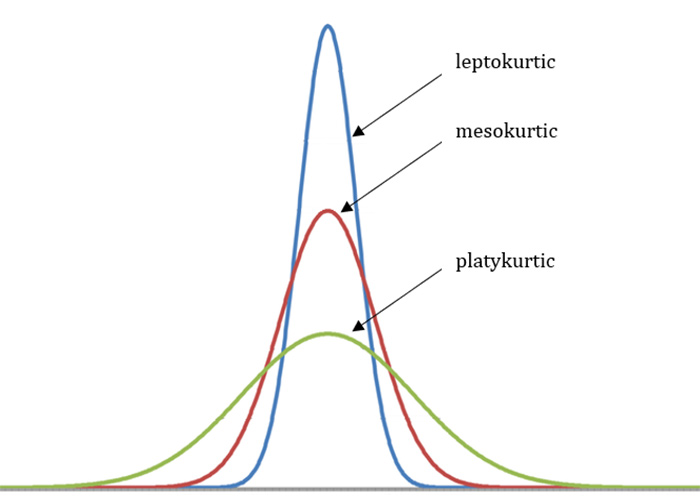
• سه دسته کشیدگی وجود دارد: مزوکورتیک (طبیعی)، پلاتیکورتیک (کمتر از نرمال)، و لپتوکورتیک (بیش از نرمال).
• ریسک Kurtosis اندازه گیری میزان تغییر چشمگیر قیمت یک سرمایه گذاری است.
• مشخصه کشیدگی یک منحنی به شما می گوید که سرمایه گذاری که ارزیابی می کنید چقدر ریسک کشیدگی دارد.

جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تحلیل آماری چیست مطالعه نمایید.

• تحلیل آماری چیست ؟

2- تعریف و مفهوم کشیدگی نمودار در آمار

کورتوسیس اندازه گیری وزن ترکیبی دم های توزیع نسبت به مرکز منحنی توزیع (میانگین) است. به عنوان مثال، هنگامی که مجموعه ای از داده های تقریباً نرمال از طریق یک هیستوگرام نمودار می شود، یک پیک زنگ را نشان می دهد، که بیشتر داده ها در سه انحراف استاندارد (به علاوه یا منفی) از میانگین قرار دارند. با این حال، هنگامی که کشیدگی بالا وجود دارد، دم‌ها بیشتر از سه انحراف استاندارد توزیع منحنی زنگوله معمولی گسترش می‌یابند.

کشیدگی گاهی اوقات با اندازه گیری اوج توزیع اشتباه گرفته می شود. با این حال، کشیدگی معیاری است که شکل دم توزیع را در رابطه با شکل کلی آن توصیف می کند. یک توزیع می تواند به شدت با کشش کم به اوج برسد و یک توزیع می تواند قله کمتری با کشیدگی زیاد داشته باشد. بنابراین، کشیدگی «دمی بودن» را اندازه‌گیری می‌کند، نه «اوج» را.

3- فرمول و محاسبه کشیدگی

1-3- محاسبه کشیدگی با صفحات گسترده (spreadsheets)

چندین روش مختلف برای محاسبه کشش وجود دارد. ساده ترین راه استفاده از فرمول Excel یا Google Sheets است. برای مثال، فرض کنید داده‌های نمونه زیر را دارید: 4، 5، 6، 3، 4، 5، 6، 7، 5، و 8 که در سلول‌های A1 تا A10 در صفحه گسترده شما قرار دارند. صفحات گسترده از این فرمول برای محاسبه کشش استفاده می کنند:

{ [ n ( n + 1 ) / ( n – 1 ) ( n – 2 ) ( n – 3 ) ] [ Σ ( xi – x̄ ) / s ]4 } – { [ 3 ( n – 1 ) 2 ] / [ ( n – 2 ) ( n – 3 ) ] }

با این حال، ما از فرمول زیر در Google Sheets استفاده می کنیم که با فرض اینکه داده ها در سلول های A1 تا A10 قرار دارند، آن را برای ما محاسبه می کند:

KURT(A1:A10)=

نتیجه کشیدگی 0.1518- است که نشان می‌دهد منحنی دارای دم‌های سبک‌تر و پلاتی کورتیک است.

2-3- محاسبه کشیدگی به صورت دستی

محاسبه کشش با دست یک تلاش طولانی است و چندین مرحله را برای رسیدن به نتایج انجام می دهد. ما از نقاط داده جدید استفاده می کنیم و تعداد آنها را برای ساده کردن محاسبه محدود می کنیم. نقاط داده جدید 27، 13، 17، 57، 113 و 25 هستند.

توجه به این نکته مهم است که حجم نمونه باید بسیار بزرگتر از این باشد. ما از شش عدد برای کاهش مراحل محاسبه استفاده می کنیم. یک قانون خوب این است که از 30 درصد داده های خود برای جمعیت های زیر 1000 نفر استفاده کنید. برای جمعیت های بزرگتر، می توانید از 10٪ استفاده کنید.

ابتدا باید میانگین را محاسبه کنید. اعداد را جمع کنید و بر شش تقسیم کنید تا به 42 برسید. سپس از فرمول های زیر برای محاسبه دو مجموع s2 (مربع انحراف از میانگین) و s4 (مربع انحراف از میانگین مربع) استفاده کنید. توجه – این اعداد نشان دهنده انحراف معیار نیستند. آنها واریانس هر نقطه داده را نشان می دهند.

s2 = Σ ( yi – ȳ )^2
s4 = Σ ( yi – ȳ )^4

که در آن:
i = Yi امین متغیر نمونه
ȳ = میانگین

برای به دست آوردن s2، از هر متغیر استفاده کنید، میانگین را کم کنید و نتیجه را مربع کنید. همه نتایج را با هم اضافه کنید:

• ²(42 – 27) = ²(15-) = 225
  ²(42 – 13) = ²(29-) = 841
  ²(42 – 17) = ²(25-) = 625
  ²(42 – 57) = ²(15) = 225
  ²(42 – 113) = ²(71) = 5041
  ²(42 – 25) = ²(17-) = 289
  225 + 841 + 625+ 225 + 5,041 + 289 = 7,246

برای بدست آوردن s4 هم به همین صورت که به توان 4 میرسد و مقدار آن برابر با 26,694,358 می شود.

حال، m2 و m4، مومنت دوم و چهارم فرمول کشش را محاسبه کنید:

m2 = s2 / n یا 7,246/6 = 1,207.67
m4 = s4 / n، یا 26,694,358/6 = 4,449,059.67

اکنون می‌توانیم کشش را با استفاده از فرمولی که در بسیاری از کتاب‌های درسی آمار یافت می‌شود، محاسبه کنیم که توزیع کاملاً نرمال با کشیدگی صفر را فرض می‌کند:

k = ( m4 / m2² ) – 3

جایی که:

k = کشیدگی
m4 = مومنت چهارم
m2 = مومنت دوم
4,449,059.67/1,458,466.83 = 3.05

بنابراین، کشش برای متغیرهای نمونه 3-3.05 یا 0.05 است.

• انحراف استاندارد چیست ؟

• واریانس چیست ؟

• تفاوت انحراف استاندارد و واریانس

4- انواع کشیدگی

سه دسته از کشیدگی وجود دارد که مجموعه‌ای از داده‌ها می‌توانند نمایش دهند: مزوکورتیک، لپتوکورتیک و پلاتیکورتیک. تمام معیارهای کشیدگی با یک منحنی توزیع نرمال مقایسه می شوند.

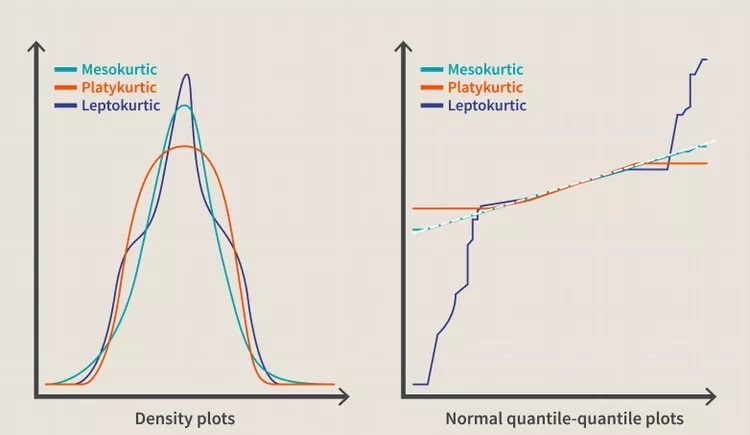
1-4- مزوکورتیک (کشیدگی = 3.0)

دسته اول کشیدگی، توزیع مزوکورتیک است. این توزیع دارای کششی مشابه با توزیع نرمال است، به این معنی که مشخصه مقدار شدید توزیع مشابه با توزیع نرمال است. بنابراین، سهام با توزیع مزوکورتیک به طور کلی سطح متوسطی از ریسک را نشان می دهد.

2-4- لپتوکورتیک (کشیدگی > 3.0)

دسته دوم توزیع لپتوکورتیک است. هر توزیعی که لپتوکورتیک باشد، کشش بیشتری نسبت به توزیع مزوکورتیک نشان می دهد. این توزیع به صورت منحنی با دنباله‌های بلند ظاهر می‌شود.

سهام با توزیع لپتوکورتیک معمولاً سطح بالایی از ریسک را نشان می‌دهد، اما احتمال بازدهی بالاتر را نشان می‌دهد، زیرا سهام معمولاً تغییرات قیمت زیادی را نشان می‌دهد.

با اینکه توزیع لپتوکورتیک ممکن است در مرکز “لاغر” باشد، اما دارای “دم های چاق” نیز می باشد.

3-4- پلاتی کورتیک (کشیدگی <3.0)

نوع نهایی توزیع، توزیع پلاتیکورتیک است. این نوع توزیع‌ها دارای دم کوتاه (پرت کمتر) هستند. توزیع‌های Platykurtic ثبات بیشتری نسبت به منحنی‌های دیگر نشان داده‌اند، زیرا تغییرات شدید قیمت در گذشته به ندرت رخ می‌داد. این به سطح کمتر از متوسط ریسک تبدیل می شود.

5- کاربرد و نحوه استفاده از کشیدگی

Kurtosis یا کشیدگی در تجزیه و تحلیل مالی برای اندازه گیری ریسک یک سرمایه گذاری از نوسانات قیمت استفاده می شود. ریسک کشیدگی با اندازه گیری های رایج تر مانند آلفا، بتا، r-squared یا نسبت شارپ متفاوت است. آلفا بازده اضافی را نسبت به یک شاخص معیار اندازه گیری می کند و بتا نوسان یک سهم را در مقایسه با بازار گسترده تر اندازه گیری می کند.

R-squared درصد حرکت یک پرتفوی یا صندوق را اندازه می گیرد که می توان آن را با یک معیار توضیح داد و نسبت شارپ بازده به ریسک را مقایسه می کند. Kurtosis میزان نوسانی را که قیمت یک سرمایه گذاری به طور مرتب تجربه کرده است را اندازه گیری می کند.

به عنوان مثال، تصور کنید یک سهم دارای قیمت متوسط 25.85 دلار برای هر سهم باشد. اگر قیمت سهام به طور گسترده و اغلب به اندازه کافی نوسان می کرد، منحنی زنگی دارای دم سنگین (کشش زیاد) خواهد بود. این بدان معنی است که تغییرات زیادی در قیمت سهام وجود دارد – یک سرمایه گذار باید نوسانات گسترده قیمت را اغلب پیش بینی کند.

اگر سهام دارای دم سبک بود (کشش کم)، سرمایه گذار ممکن است پیش بینی کند که قیمت سهام فقط گاهی اوقات نوسانات گسترده ای را تجربه می کند.

6- چرا کشیدگی مهم است؟

کورتوسیس یا کشیدگی توضیح می دهد که چقدر مشاهدات در برخی از مجموعه داده ها در دم در مقابل مرکز توزیع احتمال قرار می گیرند. در امور مالی و سرمایه گذاری، کشش اضافی به عنوان نوعی از ریسک که به عنوان “ریسک دنباله” شناخته می شود، یا احتمال وقوع زیان به دلیل یک رویداد نادر، همانطور که توسط توزیع احتمال پیش بینی می شود، تفسیر می شود. اگر چنین وقایعی بیش از پیش‌بینی‌شده توسط توزیع رایج باشد، دم‌ها «چاق» هستند.

7- کشیدگی اضافی چیست؟

در پاسخ کامل تر به سوال کشیدگی چیست باید بدانیم که کشیدگی اضافی ضریب کشیدگی را با توزیع نرمال مقایسه می کند. فرض بر این است که اکثر توزیع‌های نرمال دارای کشیدگی سه هستند، بنابراین کشیدگی اضافی بیشتر یا کمتر از سه خواهد بود. با این حال، برخی از مدل‌ها فرض می‌کنند که توزیع نرمال دارای کشیدگی صفر است، بنابراین کشیدگی اضافی بیشتر یا کمتر از صفر خواهد بود.

8- آیا کشیدگی همان چولگی یا خمیدگی است؟

نه. Kurtosis اندازه گیری می کند که چه مقدار از داده ها در یک توزیع احتمال در حول وسط (میانگین) در مقابل دم متمرکز شده اند. skewness در عوض تقارن نسبی توزیع حول میانگین را اندازه گیری می کند.

جمع بندی
Kurtosis توصیف می کند که چه مقدار از یک توزیع احتمال به جای مرکز آن در دم می افتد. در یک توزیع نرمال، کشیدگی برابر با سه (یا در برخی مدل‌ها صفر) است. کشش اضافی مثبت یا منفی شکل توزیع را بر این اساس تغییر خواهد داد. برای سرمایه گذاران، کشش در درک ریسک دنباله، یا تعداد دفعات رخ دادن رویدادهای “نادر”، با توجه به فرض فرد در مورد توزیع بازده قیمت، مهم است.