انحراف استاندارد چیست ؟

چکیده مقاله :
یکی از مباحث بسیار مهم در بحث تحلیل آماری انحراف استاندارد می باشد. در حقیقت سوال شما هم می باشد که انحراف استاندارد چیست ؟ چه کاربردی دارد ، از آن په برداشتی می توان کرد. در مسائل آماری انحراف معیار چه مفهومی را می رساند چه برداشت هایی می توان از آن کرد ؟ نحوه محاسبه آن به چه شکلی است ؟ فرمول آن چیست ؟ و خیلی سوالات دیگر که با مطالعه این مطلب به پاسخ همه این سوالات با ذکر مثال دست خواهید یافت

1- انحراف معیار چیست ؟

انحراف معیار آماری است که پراکندگی یک مجموعه داده را نسبت به میانگین آن اندازه گیری می کند و به عنوان جذر واریانس محاسبه می شود. انحراف استاندارد به عنوان جذر واریانس با تعیین انحراف هر نقطه داده نسبت به میانگین محاسبه می شود.

اگر نقاط داده دورتر از میانگین باشند، انحراف بیشتری در مجموعه داده وجود دارد. بنابراین، هر چه داده‌ها پراکنده‌تر باشند، انحراف معیار بالاتر است.

نکات کلیدی:

• انحراف استاندارد پراکندگی یک مجموعه داده را نسبت به میانگین آن اندازه گیری می کند.
• به عنوان جذر واریانس محاسبه می شود.
• انحراف استاندارد، در امور مالی، اغلب به عنوان معیاری برای ریسک نسبی یک دارایی استفاده می شود.
• یک سهام فرار دارای انحراف استاندارد بالایی است، در حالی که انحراف یک سهام با تراشه آبی پایدار معمولاً کم است.
• به عنوان یک جنبه منفی، انحراف استاندارد تمام عدم قطعیت ها را به عنوان ریسک محاسبه می کند، حتی زمانی که به نفع سرمایه گذار باشد – مانند بازده بالاتر از میانگین.

جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تحلیل آماری چیست مطالعه نمایید.

• تحلیل آماری چیست ؟

2- مفهوم انحراف استاندارد

انحراف استاندارد یک اندازه گیری آماری در امور مالی است که وقتی برای نرخ بازده سالانه یک سرمایه گذاری اعمال می شود، نوسانات تاریخی آن سرمایه گذاری را روشن می کند.

هر چه انحراف معیار اوراق بهادار بیشتر باشد، واریانس بین هر قیمت و میانگین بیشتر می شود که محدوده قیمتی بیشتری را نشان می دهد. به عنوان مثال، یک سهام فرار دارای انحراف استاندارد بالایی است، در حالی که انحراف یک سهام با تراشه آبی پایدار معمولاً کم است.

3- فرمول انحراف استاندارد

انحراف استاندارد با در نظر گرفتن جذر یک مقدار بدست آمده از مقایسه نقاط داده با میانگین جمعی یک جمعیت محاسبه می شود. فرمول این است:

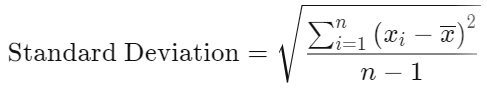
که در آن:

Xi = مقدار iام در مجموعه داده x

X = مقدار میانگین مجموعه داده ها

n = تعداد نقاط داده در مجموعه داده

4- محاسبه انحراف استاندارد

انحراف معیار به صورت زیر محاسبه می شود:

1. میانگین تمام نقاط داده را محاسبه کنید. میانگین با جمع کردن تمام نقاط داده و تقسیم آنها بر تعداد نقاط داده محاسبه می شود.
2. واریانس هر نقطه داده را محاسبه کنید. واریانس برای هر نقطه داده با کم کردن میانگین از مقدار نقطه داده محاسبه می شود.
3. مربع واریانس هر نقطه داده (از مرحله 2).
4. مجموع مقادیر واریانس مجذور (از مرحله 3).
5. مجموع مقادیر واریانس مجذور (از مرحله 4) را بر تعداد نقاط داده در مجموعه داده کمتر از 1 تقسیم کنید.
6. جذر نتیجه (از مرحله 5) را بگیرید.

5- نحوه استفاده از انحراف استاندارد

انحراف استاندارد یک ابزار مفید ویژه در استراتژی‌های سرمایه‌گذاری و معاملاتی است زیرا به اندازه‌گیری نوسانات بازار و امنیت و پیش‌بینی روند عملکرد کمک می‌کند. به عنوان مثال، از آنجایی که به سرمایه گذاری مربوط می شود، یک صندوق شاخص احتمالاً دارای انحراف استاندارد پایینی نسبت به شاخص معیار خود است، زیرا هدف صندوق تکرار این شاخص است.

از سوی دیگر، می‌توان انتظار داشت که صندوق‌های رشد تهاجمی دارای انحراف استاندارد بالایی از شاخص‌های نسبی سهام باشند، زیرا مدیران سبد آنها شرط‌بندی‌های تهاجمی را برای تولید بازدهی بالاتر از متوسط انجام می‌دهند.

انحراف استاندارد کمتر لزوماً ارجح نیست. همه چیز بستگی به سرمایه گذاری ها و تمایل سرمایه گذار به پذیرش ریسک دارد. هنگام برخورد با میزان انحراف در پرتفوی خود، سرمایه گذاران باید تحمل خود را برای نوسانات و اهداف کلی سرمایه گذاری خود در نظر بگیرند. سرمایه گذاران تهاجمی تر ممکن است با یک استراتژی سرمایه گذاری که وسایل نقلیه با نوسان بالاتر از حد متوسط را انتخاب می کند راحت باشند، در حالی که سرمایه گذاران محافظه کارتر ممکن است اینطور نباشند.

انحراف استاندارد یکی از معیارهای ریسک اساسی است که تحلیلگران، مدیران پورتفولیو و مشاوران از آن استفاده می کنند. شرکت های سرمایه گذاری انحراف معیار صندوق های سرمایه گذاری مشترک و سایر محصولات خود را گزارش می دهند. یک پراکندگی بزرگ نشان می دهد که بازده صندوق چقدر از بازده عادی مورد انتظار منحرف است. از آنجا که درک آن آسان است، این آمار به طور مرتب به مشتریان نهایی و سرمایه گذاران گزارش می شود.

6- انحراف معیار در مقابل واریانس

واریانس با گرفتن میانگین نقاط داده، تفریق میانگین از هر نقطه داده به صورت جداگانه، مربع کردن هر یک از این نتایج و سپس گرفتن میانگین دیگری از این مربع ها به دست می آید. انحراف معیار جذر واریانس است.

واریانس به تعیین اندازه گسترش داده ها در مقایسه با مقدار متوسط کمک می کند. با بزرگتر شدن واریانس، تغییرات بیشتری در مقادیر داده رخ می دهد و ممکن است شکاف بزرگتری بین یک مقدار داده و مقدار دیگر وجود داشته باشد. اگر مقادیر داده ها همه به هم نزدیک باشند، واریانس کوچکتر خواهد بود. با این حال، درک این موضوع از انحراف استاندارد دشوارتر است، زیرا واریانس‌ها یک نتیجه مربعی را نشان می‌دهند که ممکن است به طور معنی‌داری در نمودار مشابه مجموعه داده اصلی بیان نشود.

انحرافات استاندارد معمولاً برای تصویر و اعمال آسان تر است. انحراف معیار با همان واحد اندازه گیری داده ها بیان می شود که لزوماً در مورد واریانس صدق نمی کند. با استفاده از انحراف معیار، آماردانان ممکن است تعیین کنند که آیا داده ها دارای منحنی نرمال یا سایر رابطه های ریاضی هستند.

اگر داده ها در یک منحنی نرمال رفتار کنند، 68٪ از نقاط داده در یک انحراف استاندارد از میانگین یا میانگین نقطه داده قرار می گیرند. واریانس های بزرگتر باعث می شود که نقاط داده بیشتری خارج از انحراف استاندارد قرار گیرند. واریانس های کوچکتر منجر به داده های بیشتری می شود که نزدیک به میانگین است.

انحراف استاندارد به صورت گرافیکی به عنوان عرض منحنی زنگ در اطراف میانگین یک مجموعه داده نشان داده می شود. هرچه عرض منحنی بیشتر باشد، انحراف استاندارد مجموعه داده از میانگین بیشتر است.

جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تفاوت انحراف معیار و واریانس مطالعه نمایید.

• تفاوت انحراف معیار و واریانس

7- نقاط قوت انحراف معیار

انحراف استاندارد یک معیار رایج برای سنجش پراکندگی است. بسیاری از تحلیلگران احتمالاً با انحراف معیار بیشتر از سایر محاسبات آماری انحراف داده ها آشنا هستند. به همین دلیل، انحراف معیار اغلب در موقعیت‌های مختلفی از سرمایه‌گذاری گرفته تا اکچوئرها استفاده می‌شود.

انحراف معیار همه مشاهدات را شامل می شود. هر نقطه داده در تجزیه و تحلیل گنجانده شده است. اندازه‌گیری‌های دیگر انحراف مانند محدوده، تنها پراکنده‌ترین نقاط را بدون در نظر گرفتن نقاط بین آن اندازه‌گیری می‌کنند. بنابراین، انحراف معیار اغلب در مقایسه با مشاهدات دیگر، اندازه گیری قوی تر و دقیق تری در نظر گرفته می شود.

انحراف استاندارد دو مجموعه داده را می توان با استفاده از یک فرمول انحراف استاندارد ترکیبی خاص ترکیب کرد. هیچ فرمول مشابهی برای سایر اندازه گیری های مشاهده پراکندگی در آمار وجود ندارد. علاوه بر این، انحراف معیار را می توان در محاسبات جبری بیشتر بر خلاف سایر ابزارهای مشاهده استفاده کرد.

8- محدودیت های انحراف معیار

هنگام استفاده از انحراف معیار، نکات منفی وجود دارد. انحراف استاندارد در واقع میزان فاصله یک نقطه داده از میانگین را اندازه گیری نمی کند. در عوض، مربع تفاوت ها را مقایسه می کند، تفاوتی ظریف اما قابل توجه از پراکندگی واقعی از میانگین.

نقاط پرت تأثیر شدیدتری بر انحراف معیار دارند. این امر به ویژه با توجه به مجذور بودن اختلاف میانگین و در نتیجه کمیت حتی بزرگتر در مقایسه با سایر نقاط داده، صادق است. بنابراین، توجه داشته باشید که مشاهده استاندارد به طور طبیعی به مقادیر شدید وزن بیشتری می دهد.

در آخر، محاسبه دستی انحراف معیار ممکن است دشوار باشد. برخلاف سایر اندازه‌گیری‌های پراکندگی مانند محدوده (بالاترین مقدار کمتر از کمترین مقدار)، انحراف استاندارد به چندین مرحله دست و پا گیر نیاز دارد و در مقایسه با اندازه‌گیری‌های ساده‌تر، احتمال خطاهای محاسباتی بیشتری دارد. این مانع را می توان با استفاده از ترمینال بلومبرگ دور زد.

هنگام محاسبه انحراف معیار، استفاده از اکسل را در نظر بگیرید. پس از وارد کردن داده‌های خود، اگر مجموعه داده‌های شما عددی است از فرمول STDEV.S یا زمانی که می‌خواهید متن یا مقادیر منطقی را وارد کنید از STDEVA استفاده کنید. همچنین چندین فرمول خاص برای محاسبه انحراف معیار برای کل جمعیت وجود دارد.

9- مثالی از انحراف معیار

فرض کنید ما نقاط داده 5، 7، 3 و 7 را داریم که در مجموع 22 می شود. سپس 22 را بر تعداد نقاط داده تقسیم می کنیم، در این مورد مطالعاتی که به میانگین 5.5 می رسد. این منجر به تعیین‌های زیر می‌شود: x = 5.5 و N = 4.

واریانس با کم کردن مقدار میانگین از هر نقطه داده تعیین می شود و به 0.5-، 1.5، -2.5 و 1.5 می رسد. سپس هر یک از این مقادیر مجذور می شود و به 0.25، 2.25، 6.25 و 2.25 می رسد. سپس مقادیر مربع با هم جمع می شوند و مجموعاً 11 بدست می آید که سپس بر مقدار N منهای 1 که برابر با 3 است تقسیم می شود و واریانس تقریباً 3.67 حاصل می شود.

سپس جذر واریانس محاسبه می شود که به یک اندازه گیری انحراف استاندارد تقریباً 1.915 منجر می شود.

یا سهام اپل (AAPL) را برای یک دوره پنج ساله در نظر بگیرید. بازده تاریخی سهام اپل 12.49 درصد برای سال 2016، 48.45 درصد برای سال 2017، -5.39 درصد برای سال 2018، 88.98 درصد برای سال 2019 و تا سپتامبر، 60.91 درصد برای سال 2020 بوده است. بنابراین میانگین بازده طی پنج سال 4.0 درصد بوده است.

ارزش بازده هر سال کمتر از میانگین به ترتیب 28.6-، 7.36 درصد – 46.48، 47.89 درصد و 19.82 درصد بود. سپس تمام این مقادیر مربع می شوند تا 8.2٪، 0.54٪، 21.6٪، 22.93٪ و 3.93٪ به دست آید. مجموع این مقادیر 0.572 است. آن مقدار را بر 4 (N منهای 1) تقسیم کنید تا واریانس (0.572/4) = 0.143 به دست آید. جذر واریانس برای به دست آوردن انحراف استاندارد 0.3781 یا 37.81٪ گرفته می شود.

10- سوالات پرتکرار

1-10- انحراف استاندارد بالا به چه معناست؟

یک انحراف معیار بزرگ نشان می دهد که واریانس زیادی در داده های مشاهده شده حول میانگین وجود دارد. این نشان می دهد که داده های مشاهده شده کاملاً گسترده است. یک انحراف معیار کوچک یا کم نشان می‌دهد که بیشتر داده‌های مشاهده‌شده به‌شدت حول میانگین خوشه‌بندی شده‌اند.

2-10- انحراف معیار به شما چه می گوید؟

انحراف استاندارد چگونگی پراکندگی مجموعه ای از داده ها را توصیف می کند. هر نقطه داده را با میانگین تمام نقاط داده مقایسه می‌کند و انحراف استاندارد مقدار محاسبه‌شده‌ای را برمی‌گرداند که توضیح می‌دهد آیا نقاط داده در مجاورت نزدیک هستند یا اینکه پخش شده‌اند. در یک توزیع نرمال، انحراف استاندارد به شما می گوید که مقادیر چقدر از میانگین فاصله دارند.

3-10- چگونه انحراف استاندارد را به سرعت پیدا می کنید؟

اگر به توزیع برخی از داده های مشاهده شده به صورت بصری نگاه کنید، می توانید ببینید که توزیع های چاق انحراف معیار بزرگتری دارند. از طرف دیگر، اکسل بسته به مجموعه داده، توابع انحراف استاندارد را تعبیه کرده است.

4-10- چگونه انحراف معیار را محاسبه می کنید؟

انحراف معیار به عنوان جذر واریانس محاسبه می شود. روش دیگر، با یافتن میانگین یک مجموعه داده، یافتن تفاوت هر نقطه داده با میانگین، مربع کردن تفاوت ها، جمع کردن آنها با هم، تقسیم بر تعداد نقاط مجموعه داده کمتر از 1 و یافتن مربع محاسبه می شود. ریشه

5-10- چرا انحراف استاندارد مهم است؟

انحراف استاندارد مهم است زیرا می تواند به کاربران در ارزیابی ریسک کمک کند. یک گزینه سرمایه گذاری با متوسط بازده سالانه 10 درصد در سال را در نظر بگیرید. با این حال، این میانگین از بازده سه ساله گذشته 50٪، -15٪، و -5٪ به دست آمده است. با محاسبه انحراف معیار و درک احتمال کم شما برای رسیدن به میانگین 10٪ در هر سال، بهتر می توانید تصمیمات آگاهانه بگیرید و ریسک اساسی را تشخیص دهید.