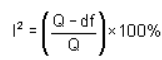ناهمسانی چیست؟ تعریف، انواع و تست های اندازه گیری

چکیده مقاله :
سیستم های اکولوژیکی ناهمگونی ذاتی دارند. تعداد فراوانی گونه ها اغلب ناهمگونی واریانس ها را در میان گروه ها یا جمعیت های مشاهده ای نشان می دهد. این اغلب با استفاده از تبدیل داده ها به دنبال تجزیه و تحلیل آماری سنتی که نیاز به همگنی دارد، مورد بررسی قرار می گیرد. چنین رویکردی زمانی بسیار مفید است که رابطه میانگین و واریانس در مجموعه داده‌ها سازگار باشد. با این حال، در برخی شرایط، رابطه میانگین و واریانس ثابت نمی ماند، به عنوان مثال، میزان تجمع فضایی موجودات می تواند در مکان و زمان تغییر کند. در این موارد، تبدیل داده‌ها به منظور «رفع» مشکل ناهمگونی می‌تواند منجر به خطای ظاهراً شدید نوع I شود. استفاده از تبدیل مدل مورد آزمون را تغییر می دهد و همچنین تأثیر مهمی بر مقیاس فضایی فرضیه دارد. استفاده از جایگزین های ناپارامتریک، مانند تست های جایگشت یا بوت استرپ، این مشکل را حل نمی کند. مدل‌های صریح این نوع تغییرات توزیعی، در جایی که رخ می‌دهند، ضروری هستند. در این مطلب سعی داریم به بررسی مفهوم و تعریف ناهمسانی پرداخته و انواع آن را به همراه تعریف ناهمسانی در واریانس و تست های اندازه گیری ناهمسانی توضیح دهیم.

ناهمسانی چیست؟

ناهمسانی چیزی نیست که از آن ترسید، فقط به این معنی است که در داده های شما تنوع وجود دارد. بنابراین، اگر مطالعه های مختلف را برای تجزیه و تحلیل آنها یا انجام یک متاآنالیز گرد هم بیاوریم، واضح است که تفاوت هایی وجود خواهد داشت. نقطه مقابل ناهمسانی یا ناهمگونی همان همسانی یا همگنی است به این معنی که همه مطالعات اثر یکسانی را نشان می‌دهند.

• تحلیل آماری

توجه به این نکته ضروری است که انواع مختلفی از ناهمسانی وجود دارد:

• بالینی: تفاوت در شرکت کنندگان، مداخلات یا نتایج
• روش شناسی: تفاوت در طراحی مطالعه، خطر سوگیری
• آماری: تنوع در اثرات یا نتایج مداخله

ما به این تفاوت‌ها علاقه‌مندیم، زیرا می‌توانند نشان دهند که مداخله ما ممکن است هر بار که از آن استفاده می‌شود به یک شکل عمل نکند. با بررسی این تفاوت‌ها، می‌توانید به درک بسیار بیشتری از اینکه چه عواملی بر مداخله تأثیر می‌گذارند، و دفعه بعد که مداخله اجرا می‌شود چه نتیجه‌ای را می‌توانید انتظار داشته باشید، برسید.

اگرچه ناهمسانی بالینی و روش شناختی مهم است، این وبلاگ بر روی ناهمسانی آماری تمرکز خواهد کرد.

در آمار، ناهمسانی مفهومی حیاتی است که در زمینه‌های مختلف ظاهر می‌شود و تعریف آن بر این اساس متفاوت است. ناهمگونی می‌تواند تفاوت‌ها را در بین نمونه‌های مستقل، بین نمونه‌ها و بین نتایج تجربی در یک متاآنالیز نشان دهد. همچنین در مورد نقض مفروضات مربوط به خطاها در مدل های خطی اعمال می شود. این پست بر روی این تعاریف آماری از ناهمگونی تمرکز دارد و به شما نشان می دهد که چگونه آن را از نظر آماری شناسایی و آزمایش کنید.

ناهمسانی واریانس چیست؟

ناهمگنی واریانس به نقض فرض همگنی واریانس، یکی از مفروضات اصلی زیربنای تجزیه و تحلیل داده های گروه بندی شده در زمینه های تک متغیره و چند متغیره اشاره دارد (به عنوان مثال، آزمون تی نمونه های مستقل، تحلیل واریانس [ANOVA]، و تحلیل واریانس چند متغیره [MANOVA]). به طور کلی، ناهمسانی واریانس به این معنی است که واریانس های جمعیتی گروه ها یا سلول های مورد مقایسه همگن یا برابر نیستند. از آنجایی که واریانس ها در محاسبه خطاهای استاندارد و عبارات خطا میانگین می شوند، با این فرض که تقریباً برابر هستند، ناهمگونی باعث ایجاد سوگیری و ناسازگاری در آزمون های اهمیت و فواصل اطمینان برای مدل مورد نظر می شود. ناهمسانی واریانس یک نمونه خاص از آن چیزی است که به عنوان ناهمگونی در زمینه رگرسیون شناخته می شود.

• رگرسیون چیست؟

• تحلیل کواریانس

به عبارت دیگر وضعیتی که در آن واریانس یک متغیر تصادفی در هر سطح یا مقدار متغیر دیگر متفاوت است. Var(y|x) برای همه مقادیر x یکسان نیست. یعنی واریانس در y تابعی از متغیر x است. ناهمگنی واریانس یکی از مفروضات اساسی تحلیل رگرسیون و سایر روش های آماری را نقض می کند. ناهمسانی نیز نامیده می شود.

• آنالیز رگرسیون

تست های شناسایی و اندازه گیری ناهمسانی

تست کره چشم Eyeball test

در طرح جنگلی forest plot خود، به جای اینکه تخمین اثر شما در کدام طرف باشد، به فواصل اطمینان همپوشانی بیندیشید. اینکه آیا نتایج در دو طرف خط بی‌تاثیری قرار دارند، ممکن است بر ارزیابی شما از وجود ناهمگونی تأثیر نگذارد، اما ممکن است بر ارزیابی شما از اهمیت ناهمگونی تأثیر بگذارد.

با در نظر گرفتن این موضوع، به نمودار زیر نگاهی بیندازید و تصمیم بگیرید که کدام نمودار همگن تر است.

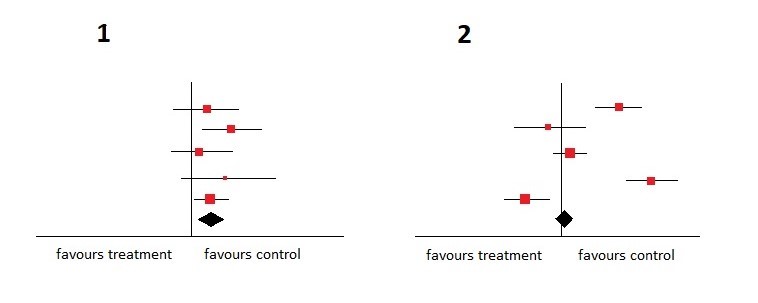
البته نمودار شماره 1 همگن تر است. فواصل اطمینان همه با هم تداخل دارند و علاوه بر آن، همه مطالعات به مداخله کنترل کمک می کنند.

برای افرادی که دوست دارند ناهمسانی را به جای نگاه کردن به آن بسنجند، نگران نباشند، هنوز روش‌های آماری وجود دارد که به شما در درک مفهوم ناهمسانی کمک می‌کند.

تست مجذور کای 2 (χ²)

این مهم است که در نظر بگیریم که نتایج مطالعات تا چه حد سازگار است. اگر فواصل اطمینان برای نتایج مطالعات فردی (که عموماً به صورت گرافیکی با استفاده از خطوط افقی نشان داده می شوند) همپوشانی ضعیفی داشته باشند، این به طور کلی وجود ناهمگنی آماری را نشان می دهد. به طور رسمی تر، یک آزمون آماری برای ناهمگنی در دسترس است. این آزمون مجذور کای (χ2 یا Chi2) در طرح‌های جنگلی در بررسی‌های کاکرین گنجانده شده است. این ارزیابی می کند که آیا تفاوت های مشاهده شده در نتایج به تنهایی با شانس سازگار است یا خیر. یک مقدار P پایین (یا یک آماره کای دو بزرگ نسبت به درجه آزادی آن) شواهدی از ناهمگونی اثرات مداخله (تغییر در تخمین اثر فراتر از شانس) ارائه می دهد.

• آزمون کای دو – توزیع کای 2 یا خی دو چیست؟

این آزمون فرضیه صفر را فرض می کند که همه مطالعات همگن هستند، یا هر مطالعه یک اثر یکسان را اندازه گیری می کند، و برای آزمایش این فرضیه به ما یک مقدار p می دهد. اگر مقدار p آزمون پایین باشد می‌توانیم فرضیه را رد کنیم و ناهمسانی وجود دارد.

از آنجایی که آزمون اغلب به اندازه کافی حساس نیست و حذف اشتباه ناهمسانی به سرعت اتفاق می‌افتد، بسیاری از دانشمندان از p-value کمتر از 0.1 به‌جای کمتر از 0.05 به عنوان برش استفاده می‌کنند.

به بیان دیگر در تفسیر آزمون مجذور کای باید دقت کرد، زیرا در موقعیت (متداول) یک متاآنالیز، زمانی که مطالعات حجم نمونه کوچکی دارند یا تعداد آنها کم است، قدرت پایینی دارد. این بدان معنی است که در حالی که یک نتیجه آماری معنی دار ممکن است نشان دهنده مشکل ناهمسانی باشد، یک نتیجه غیر معنی دار نباید به عنوان شواهدی مبنی بر عدم وجود ناهمگنی در نظر گرفته شود. همچنین به همین دلیل است که گاهی اوقات از مقدار P  کمتر از 0.10 به جای سطح معمولی 0.05 برای تعیین اهمیت آماری استفاده می شود. یکی دیگر از مشکلات این تست، که به ندرت در بررسی های کاکرین رخ می دهد، این است که وقتی مطالعات زیادی در یک متاآنالیز وجود دارد، این تست قدرت بالایی برای تشخیص مقدار کمی ناهمسانی دارد که ممکن است از نظر بالینی بی اهمیت باشد.

تست I²

این تست توسط پروفسور جولیان هیگینز توسعه داده شده است و نظریه ای برای اندازه گیری میزان ناهمگونی به جای بیان وجود یا عدم وجود آن دارد.

برخی استدلال می کنند که از آنجایی که تنوع بالینی و روش شناختی همیشه در یک متاآنالیز رخ می دهد، ناهمگونی آماری اجتناب ناپذیر است (هیگینز 2003). بنابراین آزمون ناهمسانی به انتخاب تحلیل بی ربط است. روش‌هایی برای کمی‌سازی ناسازگاری در مطالعات ایجاد شده‌اند که تمرکز را از آزمایش وجود ناهمسانی برای ارزیابی تأثیر آن بر فراتحلیل دور می‌کند. یک آمار مفید برای کمی سازی ناسازگاری برابر است با

که در آن Q آمار کای دو و df درجه آزادی آن است (هیگینز 2002، هیگینز 2003). این درصدی از تنوع در برآوردهای اثر را توصیف می کند که به جای خطای نمونه گیری (شانس) به دلیل ناهمگنی است.

آستانه برای تفسیر I2 می تواند گمراه کننده باشد، زیرا اهمیت ناسازگاری به عوامل مختلفی بستگی دارد. یک راهنمای تقریبی برای تفسیر به شرح زیر است:

• 0٪ تا 40٪: ممکن است مهم نباشد
• 30% تا 60%: ناهمگنی متوسط
• 50٪ تا 90٪: ناهمگنی قابل توجه
• 75% تا 100%: ناهمگونی قابل توجه

برای درک نظریه بالا به مثال زیر نگاه کنید.

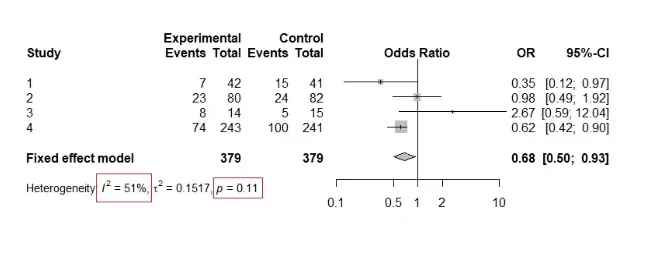
می بینیم که p-value آزمون کای اسکوئر 0.11 است که فرضیه صفر را تایید می کند و در نتیجه همگنی را نشان می دهد. با این حال، با نگاهی به مداخلات می‌توانیم برخی ناهمگونی‌ها را در نتایج مشاهده کنیم. علاوه بر این، مقدار I² 51٪ است که نشان دهنده ناهمسانی متوسط تا قابل توجه است.

این مثال خوبی از این است که چگونه آزمون χ² می‌تواند گمراه‌کننده باشد، زمانی که تنها چند مطالعه در متاآنالیز وجود دارد.

چگونه با ناهمسانی برخورد کنیم؟

هنگامی که تغییرات را در نتایج خود تشخیص دادید، باید با آن مقابله کنید. در اینجا چند مرحله برای حل این مشکل وجود دارد:

• داده های خود را برای اشتباهات بررسی کنید – به عقب برگردید و ببینید آیا ممکن است چیزی اشتباه تایپ کرده باشید
• اگر ناهمگنی خیلی زیاد است، متاآنالیز انجام ندهید – هر بررسی سیستماتیک نیاز به متاآنالیز ندارد
• کاوش ناهمسانی – این را می توان با تجزیه و تحلیل زیر گروه یا متارگرسیون انجام داد
• انجام یک متاآنالیز اثرات تصادفی – به خاطر داشته باشید که این رویکرد برای ناهمگونی است که نمی توان توضیح داد زیرا به دلیل شانس است
• تغییر معیارهای اثر – فرض کنید از تفاوت ریسک استفاده می‌کنید و ناهمگنی بالایی دارید، سپس نسبت ریسک یا نسبت شانس را امتحان کنید.

ناهمسانی در نمونه ها

وقتی از یک جامعه نمونه می گیرید، می توانید ناهمگنی آن را ارزیابی کنید. آیا داده های شما دارای تنوع هستند؟ اگر چنین است، چقدر؟ نمونه‌های ناهمگن زمانی اتفاق می‌افتند که اقلام دارای تفاوت باشند. برای ارزیابی ناهمسانی در نمونه ها می توانید از معیار پراکندگی استفاده کنید. به عنوان مثال، مقادیر انحراف استاندارد بالاتر نشان می دهد که نمونه تنوع بیشتری دارد. برعکس، مقادیر پایین تر نشان می دهد که اقلام تمایل به مشابه دارند. وقتی همگنی کامل وجود داشته باشد، تمام اشیاء در نمونه یکسان هستند و انحراف معیار برابر با صفر است. همچنین می توانید داده های خود را برای ارزیابی ناهمگنی رسم کنید.

ناهمسانی بین نمونه ها

همچنین می‌توانید در نظر بگیرید که آیا ویژگی‌های نمونه‌ها یا گروه‌های مختلف در داده‌های شما ناهمگن هستند یا خیر. هنگامی که چندین نمونه جمع آوری می کنید، آیا آنها تمایل به مشابه دارند یا متفاوت؟ در این زمینه، باید مراقب باشید که ویژگی هایی را که ارزیابی می کنید تعریف کنید. برخی از خواص نمونه های مختلف می توانند ناهمگن باشند، در حالی که برخی دیگر همگن هستند. در این بخش، به شما نشان می‌دهیم که چگونه ناهمگنی بین نمونه‌ها را برای داده‌های پیوسته و طبقه‌بندی ارزیابی کنید.

• انواع داده ها در آمار

داده های پیوسته

با داده های پیوسته، می توانید ناهمسانی بین میانگین نمونه و تنوع را ارزیابی کنید. با استفاده از باکس‌پلات‌ها، می‌توانید ویژگی‌های آن‌ها را نمایش دهید و تعیین کنید که آیا داده‌ها ناهمگن هستند یا خیر.

در حالی که این نمودارها به صورت بصری ناهمگونی در داده ها را نشان می دهند، شما می توانید این ویژگی ها را با استفاده از آزمون های فرضیه های آماری آزمایش کنید.

به عنوان مثال، ANOVA میانگین چند نمونه را مقایسه می کند. ناهمگونی میانگین های گروهی را آزمایش می کند. با این حال، آزمون F-test ANOVA فرض می‌کند که تنوع گروه‌ها برابر است. به عبارت دیگر، زمانی که میانگین های گروه ناهمگن هستند، می توانید از ANOVA استفاده کنید، اما تغییرپذیری باید همگن باشد.

برای تعیین اینکه آیا میانگین های گروه از نظر آماری ناهمگن هستند، از آزمون های فرضیه مانند آزمون t و ANOVA یک طرفه استفاده کنید. برای ارزیابی اینکه آیا تنوع در گروه متفاوت است، از آزمون واریانس استفاده کنید.

داده های طبقه بندی شده

برای داده های طبقه بندی شده، می توانید ناهمگونی دسته ها را ارزیابی کنید. ما آب نبات های M&M را برای این نمونه ها در نظر می گیریم که شش رنگ دارند: قهوه ای، زرد، سبز، قرمز، نارنجی و آبی.

مجدداً به تفاوت بین ناهمگونی در یک نمونه در مقابل بین نمونه توجه کنید.

یک نمونه M&M اگر فقط یک رنگ داشته باشد همگن خواهد بود. با افزایش تعداد رنگ ها، نمونه به طور فزاینده ای ناهمگن می شود.

با این حال، برای نمونه های متعدد، همگنی زمانی رخ می دهد که تعداد و نسبت رنگ ها بین آنها یکسان باشد. دسته های ناهمگن نسبت رنگ متفاوتی خواهند داشت.

شما می توانید این را از نظر آماری برای داده های طبقه بندی با استفاده از آزمون مجذور کای برای همسانی آزمایش کنید. وقتی مقدار p شما پایین است، فرضیه صفر (همگنی) را رد کنید و نتیجه بگیرید که نمونه ها ناهمگن هستند. تفاوت‌های بین نسبت‌های دسته‌بندی به اندازه‌ای متفاوت است که از نظر آماری معنی‌دار باشد.

محاسبات همگنی آزمون کای دو همانند آزمون استقلال است. تفاوت بین آنها در فرضیه ها، منطق آزمون و روش های نمونه گیری نهفته است.

ناهمسانی بین مطالعات علمی

هنگامی که یک سری مطالعات علمی را در نظر می گیرید که همگی تلاش می کنند به یک سوال تحقیقاتی پاسخ دهند، می توانید ناهمگونی نتایج آنها را ارزیابی کنید. متاآنالیز چیزی بیش از گزارش صرف میانگین اندازه اثر برای مجموعه ای از مطالعات انجام می دهد. این نوع تجزیه و تحلیل، تنوع اندازه‌های اثر را از مطالعات فردی حول اثر میانگین کلی نیز در نظر می‌گیرد – جایی که ناهمسانی به وجود می‌آید!

در حالت ایده آل، نتایج مطالعه همه مشابه (یعنی همگن) هستند. وقتی این درست باشد، همه آنها یک تصویر را ترسیم می کنند و به شما در مورد اثر واقعی اعتماد به نفس می دهند. با این حال، اگر نتایج ناهمگن هستند، باید با دقت پیش بروید و تفاوت‌های بین یافته‌ها را درک کنید. شما همچنین می خواهید درجه ناهمسانی را ارزیابی کنید. آیا مطالعات تفاوت زیادی دارند یا فقط اندکی؟

یک روش گرافیکی و عددی برای ارزیابی ناهمگونی در یک متاآنالیز به شما نشان خواهیم داد.

نمودارهای جنگلی

نمودار جنگلی که به عنوان بلوبوگرام نیز شناخته می شود، یک نمودار تخصصی است که برای نمایش نتایج مطالعات مختلف در یک متاآنالیز طراحی شده است. این نمودارها اندازه افکت‌ها را در محور افقی نشان می‌دهند و شامل یک خط مرجع برای بدون اثر هستند. برای هر آزمایش، یک تخمین نقطه ای برای اثر و یک فاصله اطمینان (CI) نمایش می دهد. برای ارزیابی ناهمسانی در یک متاآنالیز می توانید از نمودار جنگلی استفاده کنید.

آمار I²

آماره I² درجه ناهمسانی را در یک سری مطالعات در یک متاآنالیز کمیت می دهد. این آمار درصدی است که از 0 تا 100 درصد متغیر است. این نسبت تغییرات حول اندازه اثر واقعی به غیر از خطای نمونه گیری را نشان می دهد. در بخش های قبل این آزمون با جزئیات بیشتری توضیح داده شده است.