روش ژاکوبی در متلب همراه با کد، مزایا و کاربرد

چکیده مقاله:
روش ژاکوبی در متلب (The Jacobian Method in MATLAB) که با نام روش تکراری ژاکوبی نیز شناخته می شود، یک الگوریتم اساسی برای حل دستگاه های معادلات خطی می باشد. این روش که به نام ریاضیدان کارل گوستاو ژاکوب ژاکوبی نامگذاری شده است، به ویژه در مواجهه با سیستم های بزرگ که در آنها استفاده از روش های مستقیم از نظر محاسباتی، پرهزینه می باشد، کاربرد دارد. این روش با بهره گیری از ویژگی های ماتریس ها، راه حلی کارآمد ارائه می دهد و با تجزیه یک مجموعه پیچیده از معادلات به بخش های ساده تر عمل می کند و یافتن تقریب های حل را آسان تر می سازد.

برای درک ساده این روش، فرض کنید مجموعه ای از معادلات دارید و باید مقادیر متغیرهایی را بیابید که همزمان تمام این معادلات را برقرار کنند. به جای حل تمامی معادلات به طور همزمان، این روش با یک حدس اولیه برای مقادیر متغیرها شروع می کند. سپس در هر مرحله این حدس را اصلاح کرده و با هر تکرار به مقدار دقیق تر نزدیک تر می شود.
در ادامه به بررسی اصول، کاربردها، مزایا کد متلب روش ژاکوبی می پردازیم و اهمیت آن را در ریاضیات محاسباتی و رشته های مهندسی مشخص می کنیم.

روش ژاکوبی در متلب چیست؟

این راه حل، یک الگوریتم تکراری برای حل دستگاه های معادلات خطی است و به ویژه برای سیستم های بزرگ که در آن ها استفاده از روش های مستقیم (مانند حذف گوسی) از نظر محاسباتی پرهزینه می باشد، کاربرد دارد. این روش به نام کارل گوستاو ژاکوب ژاکوبی، ریاضیدان آلمانی، نامگذاری شده است.

روش ژاکوبی در متلب یکی از روش های تکراری برای حل دستگاه معادلات خطی است. این روش بر پایه تفکیک ماتریس ضرایب به صورت جمعی از یک ماتریس قطری و باقی ماتریس ها بنا شده است. در روش ژاکوبی، مقدار هر مجهول در یک تکرار جدید، تنها بر اساس مقادیر قبلی سایر مجهولات محاسبه می شود. این روش زمانی همگرا می شود که ماتریس ضرایب به صورت قطری غالب باشد، به این معنا که قدر مطلق عناصر قطری آن از مجموع قدر مطلق سایر عناصر در هر سطر بزرگتر باشد. روش ژاکوبی به دلیل قابلیت اجرای همزمان هر معادله به صورت مستقل، در پردازش موازی کاربرد دارد، اما گاهی ممکن است نسبت به روش های مستقیم مثل گاوس سریع تر همگرا نشود.

• نرم افزار متلب چیست؟

در متلب، روش ژاکوبی را می توان با یک کد ساده پیاده سازی کرد. ابتدا ماتریس ضرایب و بردار جواب ها را تعریف می کنیم و سپس یک مقدار اولیه برای متغیرهای مجهول در نظر می گیریم. در هر تکرار، مقدار جدید متغیرها با استفاده از فرمول ژاکوبی محاسبه می شود تا زمانی که تغییرات بین دو تکرار متوالی کمتر از مقدار مشخصی شود. در نهایت، الگوریتم مقادیر تقریبی مجهولات را برمی گرداند. این روش برای دستگاه های خطی بزرگ که حل مستقیم آنها پرهزینه است، گزینه مناسبی می باشد، اما سرعت همگرایی آن وابسته به ساختار ماتریس ضرایب است.

• شبیه سازی با متلب

مبانی روش ژاکوبی در متلب

این روش برای حل دستگاه معادلات خطی به صورت زیر استفاده می شود:

Ax = b

که در آن:

• A یک ماتریس مربعی است،
• x بردار مجهولات می باشد،
• b بردار سمت راست معادله است.

این روش ماتریس A را به دو بخش تجزیه می کند:

• D که مؤلفه قطر اصلی ماتریس است،
• R که سایر بخش های ماتریس را در بر می گیرد،

به طوری که:

A = D + R

با استفاده از این تجزیه، دستگاه معادلات به صورت زیر بازنویسی می شود:

Dx = b − Rx

فرمول تکراری این متد به صورت زیر است:

که در آن x^k تقریب مقدار مجهولات در مرحله kام است.

• شبیه سازی

نحوه اجرا روش تکراری ژاکوبی در متلب

روش تکراری ژاکوبی یک پیاده سازی خاص از روش ژاکوبی است. این روش فرض می کند که دستگاه معادلات خطی را می توان به صورت Ax = b نوشت، که در آن:

• A ماتریس ضرایب است،
• x بردار متغیرهای مجهول،
• b بردار ضرایب ثابت می باشد.

• شبیه سازی مونت کارلو چیست؟

مرحله اول: مقدار دهی اولیه

روش تکراری ژاکوبی برای حل دستگاه معادلات خطی $Ax=b$ نیاز به یک مقدار اولیه برای بردار مجهولات دارد. ابتدا ماتریس A و بردار b را تعریف کرده و یک مقدار اولیه برای بردار جواب x در نظر می گیریم. معمولاً مقدار اولیه به صورت صفر یا یک بردار حدسی انتخاب می شود. همچنین یک مقدار برای خطای مجاز یا تعداد تکرارهای مورد نظر مشخص می کنیم.

مرحله دوم: اعمال فرمول تکراری

در هر تکرار، مقدار جدید هر درایه از بردار x بر اساس مقدار قبلی سایر درایه ها محاسبه می شود. این مقدار از فرمول زیر به دست می آید:

مرحله سوم: بررسی شرط توقف

بعد از هر تکرار، معیار همگرایی بررسی می شود. معمولاً از نُرم اختلاف بین دو بردار متوالی یا نُرم باقی مانده استفاده می شود.

این کد روش تکراری ژاکوبی را پیاده سازی می کند و در نهایت مقدار تقریبی x را نمایش می دهد.

مفروضات روش ژاکوبی

روش تکراری ژاکوبی برای حل دستگاه معادلات خطی دارای چند مفروضه اساسی می باشد که باید رعایت شوند تا روش به درستی عمل کند و به جواب همگرا شود. این مفروضات عبارتند از:

1. وجود جواب یکتا: دستگاه معادلات خطی Ax = b باید دارای یک جواب یکتا باشد. این شرط معمولاً زمانی برقرار است که ماتریس ضرایب A معکوس پذیر باشد، یعنی دترمینان آن برابر صفر نباشد. در غیر این صورت، ممکن است دستگاه دارای بی نهایت جواب یا فاقد جواب باشد که در این حالت روش ژاکوبی کارایی نخواهد داشت.
   نمایش کپی در حافظه

   نمایش کدif det(A) == 0 error('ماتریس A منفرد است و دستگاه معادلات ممکن است جواب یکتا نداشته باشد.'); end
2. عدم وجود صفر در قطر اصلی ماتریس: عناصر واقع در قطر اصلی ماتریس ضرایب A نباید مقدار صفر داشته باشند، زیرا در فرآیند محاسبه مقدار جدید متغیرها، هر عنصر از بردار مجهولات بر مقدار قطر اصلی ماتریس تقسیم می شود. در صورتی که مقدار صفر در قطر اصلی وجود داشته باشد، عملیات تقسیم بر صفر رخ داده و محاسبات دچار خطا خواهد شد.
   نمایش کپی در حافظه

   نمایش کدif any(diag(A) == 0) error('ماتریس A دارای عنصر صفر در قطر اصلی می باشد که باعث تقسیم بر صفر خواهد شد.'); end
3. شرط قطری غالب: برای این که روش ژاکوبی همگرا باشد، ماتریس ضرایب A باید قطری غالب باشد، یعنی برای هر سطر مقدار قدرمطلق عنصر واقع در قطر اصلی بزرگ تر یا برابر مجموع قدرمطلق سایر عناصر آن سطر باشد:
   نمایش کپی در حافظه

   نمایش کدis_diagonally_dominant = all(2 * abs(diag(A)) >= sum(abs(A), 2)); if ~is_diagonally_dominant warning('ماتریس A به صورت قطری غالب نیست، روش ژاکوبی ممکن است همگرا نشود.'); end

اگر این شرط برای تمامی سطرها برقرار باشد، روش ژاکوبی به طور تضمینی همگرا خواهد شد. در غیر این صورت، ممکن است روش به جواب صحیح نرسد یا سرعت همگرایی آن بسیار کند باشد.

• شبیه سازی بازوی ربات با متلب

مثال کد متلب روش ژاکوبی

jacobian(f, v) ماتریس ژاکوبی تابع f را نسبت به v محاسبه می کند. هر درایه (i, j) از این ماتریس برابر است با:

مثال یک: ماتریس ژاکوبی یک تابع برداری

ماتریس ژاکوبی یک تابع برداری، ماتریسی متشکل از مشتقات جزئی آن تابع است .محاسبه ماتریس ژاکوبی برای تابع [x*y*z, y^2, x + z] نسبت به بردار [x, y, z]:

نتیجه:

همچنین، اگر متغیرها را به شکل ستونی [x; y; z] تعریف کنیم، ماتریس ژاکوبی تغییری نخواهد کرد.

ماتریس ژاکوبی نسبت به نحوه ارائه بردار دوم در ورودی تابع (jacobian) به ‌صورت سطری یا ستونی تغییر نمی کند. این خاصیت نشان می دهد که ساختار ماتریس ژاکوبی به نحوه تعریف بردار متغیرها حساس نیست.

مثال دو: ماتریس ژاکوبی یک تابع عددی (اسکالر)

ماتریس ژاکوبی یک تابع عددی برابر با گرادیان آن به‌صورت سطری است.

محاسبه ژاکوبی برای تابع 2x + 3y + 4*z نسبت به [x, y, z]:

محاسبه گرادیان همین تابع:

مثال سوم: ژاکوبی نسبت به یک متغیر اسکالر

ژاکوبی یک تابع نسبت به یک متغیر اسکالر، برابر با مشتق اول آن تابع است. برای یک تابع برداری، ژاکوبی نسبت به یک اسکالر برداری از مشتقات اول را می دهد

محاسبه ژاکوبی برای تابع [x^2y, xsin(y)] نسبت به x:

مقایسه با مشتقات مستقیم:

نتیجه همان مقدار قبلی است.

شرایط همگرایی روش ژاکوبی

روش ژاکوبی برای همه دستگاه‌های معادلات همگرا نیست. یکی از شرایط همگرایی این روش قطری غالب بودن ماتریس A است، یعنی برای هر سطر:

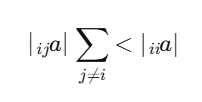
اگر این شرط برقرار نباشد، ممکن است روش ژاکوبی همگرا نشود یا به کندی همگرا گردد.

روش ژاکوبی در متلب یکی از روش های عددی برای حل دستگاه های معادلات خطی است که بر پایه تکرار بنا شده است. برای این که این روش همگرا باشد، ماتریس ضرایب باید دارای خاصیت قطری غالب باشد، به این معنی که قدر مطلق هر درایه قطری از مجموع قدر مطلق سایر درایه های همان سطر بزرگ تر باشد. این شرط تضمین می کند که مقادیر به دست آمده در هر مرحله از تکرار به مقدار دقیق همگرا شوند. اگر این شرط برقرار نباشد، ممکن است روش ژاکوبی به جواب درستی نرسد یا به کندی همگرا شود.

علاوه بر شرط قطری غالب، روش ژاکوبی تحت شرایط خاصی می تواند در ماتریس های متقارن و مثبت معین نیز همگرا باشد. در غیر این صورت، تغییر در ترتیب معادلات یا استفاده از روش های پیشرفته تر مانند روش گوس سایدل توصیه می شود. همچنین مقدار اولیه انتخاب شده نیز بر نرخ همگرایی تأثیر دارد، به طوری که مقدار اولیه مناسب می تواند باعث افزایش سرعت همگرایی شود. در مسائل عملی، برای بررسی همگرایی این روش معمولاً از معیارهایی مانند اختلاف بین تکرارهای متوالی یا خطای نسبی استفاده می شود.

• کاربرد متلب در ریاضیات

مزایای روش ژاکوبی در متلب

روش ژاکوبی یکی از روش های عددی ساده و کارآمد برای حل دستگاه معادلات خطی است که مزایای متعددی دارد. در ادامه به بررسی مهم ترین مزایای این روش می پردازیم.

• مزایا و معایب زبان برنامه نویسی متلب

سادگی پیاده سازی

پیاده سازی روش ژاکوبی در متلب بسیار آسان است، زیرا این روش تنها نیاز به اجرای چندین تکرار از یک فرمول بازگشتی دارد. در این روش، مقدار جدید هر متغیر بر اساس مقادیر قبلی سایر متغیرها محاسبه می شود که باعث می شود الگوریتم آن ساده و قابل فهم باشد. این سادگی باعث می شود که روش ژاکوبی به راحتی در محیط های برنامه نویسی مانند متلب اجرا شود و برای آموزش و پژوهش در حوزه حل دستگاه های معادلات خطی مورد استفاده قرار گیرد.

مناسب برای ماتریس های بزرگ و پراکنده

روش های مستقیم مانند حذف گاوسی و LU Decomposition به دلیل نیاز به ذخیره سازی مقادیر زیاد، برای ماتریس های بزرگ و پراکنده چندان مناسب نیستند. در مقابل، روش ژاکوبی از آنجایی که در هر تکرار تنها از مقادیر قبلی متغیرها استفاده می کند، فضای حافظه کمتری را اشغال می نماید. این ویژگی، روش ژاکوبی را به گزینه ای ایده آل برای حل دستگاه معادلات خطی که دارای ماتریس های بزرگ و پراکنده هستند، تبدیل می کند.

قابلیت محاسبه موازی (Parallel Computation)

یکی از ویژگی های بارز روش ژاکوبی این است که مقدار جدید هر متغیر فقط به مقادیر قبلی وابسته است و نیازی به محاسبه مقادیر جدید به صورت ترتیبی ندارد. این خاصیت باعث می شود که روش ژاکوبی به راحتی به صورت موازی (Parallel Processing) اجرا شود. در پردازنده های چند هسته ای و همچنین در محاسبات مبتنی بر GPU، امکان اجرای همزمان محاسبات برای متغیرهای مختلف وجود دارد که موجب افزایش سرعت اجرای الگوریتم می شود. این ویژگی روش ژاکوبی را به یک گزینه مناسب برای سیستم هایی که نیاز به پردازش سریع دارند، تبدیل می کند.

عدم نیاز به تغییر شکل ماتریس اصلی

برخلاف برخی از روش های عددی دیگر، روش ژاکوبی نیازی به انجام عملیات بازآرایی (Pivoting) یا فاکتورگیری ندارد. در روش های مستقیم مانند حذف گاوسی، ممکن است نیاز باشد که سطرها یا ستون های ماتریس برای جلوگیری از بروز خطاهای عددی تغییر داده شوند، اما در روش ژاکوبی چنین نیازی وجود ندارد. این موضوع باعث می شود که ساختار اصلی ماتریس در طول فرآیند حل حفظ شود و پیچیدگی محاسباتی کاهش یابد.

کاربرد در سیستم های غیرخطی و مدل های عددی

روش ژاکوبی علاوه بر حل دستگاه های معادلات خطی، در حل برخی از سیستم های غیرخطی و روش های عددی نیز کاربرد دارد. به عنوان مثال، این روش می تواند به عنوان بخشی از حل سیستم های غیرخطی در روش های تکراری مانند گوسی-ژاکوبی مورد استفاده قرار گیرد. همچنین، در مدل سازی های عددی که نیاز به حل تکراری معادلات دارند، روش ژاکوبی می تواند به عنوان یک رویکرد موثر و ساده مورد استفاده قرار گیرد.

معایب روش ژاکوبی در متلب

روش ژاکوبی علاوه بر مزایای خود، دارای محدودیت ها و معایبی نیز می باشد که ممکن است در برخی از مسائل عددی باعث کاهش کارایی آن شود. در ادامه به بررسی مهم ترین معایب این روش می پردازیم.

• مشاوره برنامه نویسی

عدم همگرایی در همه موارد

روش ژاکوبی برای تمامی ماتریس ها همگرا نمی شود. به طور خاص، اگر ماتریس ضرایب دارای خاصیت قطری غالب نباشد، ممکن است روش دچار واگرایی شود یا همگرایی آن بسیار کند باشد. ماتریس قطری غالب ماتریسی است که در آن مقدار مطلق هر عنصر قطری بزرگ تر از مجموع قدر مطلق سایر عناصر موجود در همان سطر باشد. در غیر این صورت، روش ژاکوبی ممکن است نتواند به یک جواب پایدار برسد و حتی پس از انجام تعداد زیادی تکرار، تغییرات مقادیر متغیرها متوقف نشود.

سرعت همگرایی پایین

در مقایسه با روش های دیگر مانند گوس-سایدل، روش ژاکوبی معمولاً سرعت همگرایی پایین تری دارد. این موضوع به ویژه زمانی که دستگاه معادلات دارای شرایط عددی بد باشد، مشهودتر است. در روش ژاکوبی، مقادیر جدید متغیرها تنها بر اساس مقادیر قبلی تعیین می شوند، در حالی که در روش هایی مانند گوس-سایدل، از مقادیر جدید محاسبه شده در همان مرحله نیز استفاده می شود که این امر باعث افزایش سرعت همگرایی می گردد. به همین دلیل، روش ژاکوبی ممکن است برای حل برخی دستگاه های معادلات گزینه مناسبی نباشد.

نیاز به تعداد زیادی تکرار در برخی موارد

در حالی که روش های مستقیم مانند حذف گاوسی و فاکتورگیری LU می توانند جواب دقیق را در تعداد محدودی از عملیات به دست آورند، روش ژاکوبی یک روش تکراری است که ممکن است نیاز به تعداد زیادی تکرار داشته باشد تا به مقدار مورد نظر همگرا شود. این مسئله به خصوص در شرایطی که دقت بالایی مورد نیاز باشد، می تواند منجر به افزایش زمان محاسباتی شود. در نتیجه، برای مسائل بزرگ و پیچیده، این روش ممکن است از نظر کارایی نسبت به سایر روش های عددی عملکرد ضعیف تری داشته باشد.

حساسیت به مقدار اولیه

یکی دیگر از معایب روش ژاکوبی، حساسیت آن به مقدار اولیه انتخاب شده برای متغیرها می باشد. مقدار اولیه مناسب می تواند فرآیند همگرایی را تسریع کند، در حالی که انتخاب مقادیر نامناسب ممکن است منجر به نوسان در مقدارهای محاسبه شده یا حتی کند شدن روند حل شود. در برخی موارد، مقدارهای اولیه نادرست ممکن است باعث شوند که روش ژاکوبی به جای نزدیک شدن به جواب، دچار رفتار نوسانی یا واگرایی شود. بنابراین، انتخاب مقدار اولیه مناسب یکی از نکات مهم در استفاده از این روش می باشد.

حساسیت به خطاهای عددی

روش ژاکوبی در شرایطی که دقت عددی بسیار مهم است، ممکن است دچار خطای گرد کردن شود. این مسئله زمانی بیشتر دیده می شود که دستگاه معادلات شامل مقدارهای بسیار بزرگ یا بسیار کوچک باشد. در چنین شرایطی، عملیات محاسباتی می تواند دقت خود را از دست بدهد و منجر به بروز خطاهای عددی شود که در نهایت باعث کاهش دقت نتایج به دست آمده خواهد شد. این حساسیت به خطاهای عددی یکی از دلایلی است که روش ژاکوبی برای حل مسائل با دقت بسیار بالا توصیه نمی شود.

با در نظر گرفتن این معایب، روش ژاکوبی تنها در شرایط خاص و برای مسائل خاصی می تواند گزینه مناسبی باشد. در بسیاری از موارد، روش های جایگزین مانند گوس-سایدل یا روش های مستقیم می توانند عملکرد بهتری داشته باشند.

کاربردهای ماتریس ژاکوبی در متلب

ماتریس ژاکوبی یکی از مفاهیم کلیدی در ریاضیات عددی و محاسبات مهندسی است که در بسیاری از حوزه ها کاربرد دارد. در متلب، این ماتریس برای حل مسائل مختلفی مانند سیستم های غیرخطی، بهینه سازی، رباتیک و تحلیل معادلات دیفرانسیل مورد استفاده قرار می گیرد. در ادامه به بررسی مهم ترین کاربردهای آن می پردازیم.

سیستم های غیرخطی

یکی از مهم ترین کاربردهای ماتریس ژاکوبی در حل سیستم های غیرخطی است. در روش نیوتن-رافسون که یک روش عددی پرکاربرد برای یافتن ریشه های معادلات غیرخطی می باشد، از ماتریس ژاکوبی برای تقریب زدن رفتار سیستم در نزدیکی یک نقطه استفاده می شود. این ماتریس که شامل مشتقات جزئی توابع نسبت به متغیرهای مختلف است، به عنوان یک ابزار اساسی در تعیین جهت و میزان اصلاح مقادیر اولیه به کار می رود. استفاده از ماتریس ژاکوبی در این روش باعث افزایش دقت و سرعت همگرایی می شود و امکان یافتن جواب های دقیق تری را فراهم می کند.

بهینه سازی

ماتریس ژاکوبی در بسیاری از الگوریتم های بهینه سازی مبتنی بر گرادیان نقش اساسی دارد. در روش هایی مانند نزول گرادیان (Gradient Descent) و الگوریتم های شبه نیوتنی، این ماتریس برای محاسبه نرخ تغییر تابع هدف نسبت به متغیرهای تصمیم گیری استفاده می شود. با استفاده از اطلاعات حاصل از ماتریس ژاکوبی، می توان مسیر حرکت در فضای پارامترها را مشخص کرد و به سمت نقطه بهینه حرکت نمود. این ویژگی به خصوص در مسائل بهینه سازی غیرخطی که دارای چندین متغیر هستند، اهمیت بیشتری پیدا می کند.

رباتیک و سینماتیک

در زمینه رباتیک، ماتریس ژاکوبی برای تحلیل سینماتیک مستقیم و معکوس ربات ها استفاده می شود. این ماتریس رابطه بین سرعت مفاصل ربات و سرعت خطی و زاویه ای قسمت انتهایی آن را توصیف می کند. به عبارت دیگر، با استفاده از ماتریس ژاکوبی می توان بررسی کرد که چگونه تغییرات در مفاصل ربات بر موقعیت و جهت گیری نهایی بازوی ربات تأثیر می گذارد. این کاربرد در کنترل ربات ها، برنامه ریزی مسیر و جلوگیری از برخورد با موانع اهمیت ویژه ای دارد.

معادلات دیفرانسیل

یکی دیگر از کاربردهای مهم ماتریس ژاکوبی در تحلیل پایداری سیستم های دینامیکی می باشد. در مطالعه معادلات دیفرانسیل معمولی و سیستم های دینامیکی، این ماتریس برای بررسی رفتار سیستم در نقاط تعادل مورد استفاده قرار می گیرد. مقادیر ویژه ماتریس ژاکوبی در این نقاط می توانند اطلاعات مفیدی درباره پایداری سیستم ارائه دهند. اگر تمامی مقادیر ویژه دارای قسمت حقیقی منفی باشند، سیستم پایدار است، اما اگر حداقل یکی از آن ها دارای قسمت حقیقی مثبت باشد، سیستم ناپایدار خواهد بود. این تحلیل در مهندسی کنترل، دینامیک سیالات، زیست شناسی ریاضی و بسیاری از شاخه های علمی دیگر کاربرد دارد.

ماتریس ژاکوبی به دلیل ویژگی های خاص خود، ابزاری قدرتمند در مدل سازی و حل مسائل پیچیده ریاضی و مهندسی محسوب می شود و در متلب به طور گسترده مورد استفاده قرار می گیرد.