آزمون Mann Whitney U: تعریف، مفروضات و مثال

چکیده مقاله:
آزمون Mann Whitney U یکی از روش های ناپارامتری برای مقایسه دو گروه مستقل است. این آزمون زمانی استفاده می شود که داده ها از توزیع نرمال پیروی نکنند یا حجم نمونه کوچک باشد. برخلاف آزمون t مستقل که فرض توزیع نرمال داده ها را دارد، آزمون Mann-Whitney U بر رتبه بندی داده ها تکیه می کند و میزان تفاوت بین دو گروه را بر اساس چیدمان مقادیر بررسی می نماید. این روش به ویژه در پژوهش های علوم اجتماعی، پزشکی و زیست شناسی که داده های عددی ولی غیر نرمال دارند، کاربرد گسترده ای دارد.
در آزمون Mann-Whitney U فرض صفر بیان می کند که توزیع مقادیر در دو گروه یکسان است و تفاوت معناداری بین آن ها وجود ندارد. در مقابل، فرض مقابل نشان می دهد که یکی از گروه ها به طور معناداری دارای مقادیر بالاتر یا پایین تر از گروه دیگر است. این آزمون از طریق محاسبه مجموع رتبه های داده ها در هر گروه و مقایسه آن ها، تصمیم گیری می کند. با توجه به عدم نیاز به فرض نرمال بودن داده ها، Mann-Whitney U به عنوان جایگزینی مناسب برای آزمون های پارامتری در شرایطی که فرض های آن ها برقرار نیست، شناخته می شود.
آزمون Mann Whitney U چیست؟
آزمون Mann Whitney U، که با نام آزمون رتبهای ویلکاکسون (Wilcoxon Rank) نیز شناخته می شود، یک آزمون آماری ناپارامتریک است که برای مقایسه دو نمونه یا گروه استفاده می شود.
این آزمون بررسی می کند که آیا دو گروه نمونه گیری شده احتمالاً از یک جمعیت، منشأ گرفته اند یا خیر و اساساً این سؤال را مطرح می کند که آیا این دو جمعیت از نظر توزیع داده ها شکل مشابهی دارند؟ به عبارت دیگر، هدف این آزمون یافتن شواهدی است که نشان دهد آیا گروه ها از جمعیت هایی با سطوح مختلف یک متغیر مورد نظر استخراج شده اند یا نه. بر این اساس، فرضیات آزمون Mann-Whitney U به شرح زیر می باشند:
- فرض صفر: (H0) دو جمعیت برابر هستند.
- فرض جایگزین: (H1) دو جمعیت برابر نیستند.
برخی از پژوهشگران این آزمون را به عنوان روشی برای مقایسه میانه های دو جمعیت تفسیر می کنند، در حالی که آزمون های پارامتریک، مانند آزمون t ، میانگین های دو گروه مستقل را مقایسه می کنند. در شرایط خاصی که داده ها دارای توزیع مشابهی باشند (با رعایت مفروضات)، این تفسیر معتبر است. با این حال، باید توجه داشت که میانه ها مستقیماً در محاسبات آماره آزمون Mann Whitney U دخالت ندارند. در واقع، ممکن است دو گروه دارای میانه های یکسان باشند اما طبق این آزمون از نظر آماری تفاوت معنی داری داشته باشند.

آزمون The Mann Whitney U
آزمون Mann Whitney U برای مقایسه تفاوت های بین دو گروه مستقل زمانی که متغیر وابسته ترتیبی یا پیوسته باشد اما توزیع نرمال نداشته باشد، مورد استفاده قرار می گیرد. به عنوان مثال، می توان از این آزمون برای بررسی اینکه آیا نگرش نسبت به تبعیض در پرداخت، که در مقیاس ترتیبی اندازه گیری می شود، بر اساس جنسیت تفاوت دارد یا خیر، استفاده کرد (در این حالت، متغیر وابسته “نگرش نسبت به تبعیض در پرداخت” و متغیر مستقل “جنسیت” با دو گروه “مرد” و “زن” خواهد بود). همچنین، این آزمون می تواند برای بررسی تفاوت حقوق، که در مقیاس پیوسته اندازه گیری می شود، بر اساس سطح تحصیلات به کار رود (در این حالت، متغیر وابسته “حقوق” و متغیر مستقل “سطح تحصیلات” با دو گروه “دیپلم” و “دانشگاه” خواهد بود).
آزمون Mann Whitney U اغلب به عنوان جایگزین ناپارامتریک آزمون t مستقل در نظر گرفته می شود، اگرچه این موضوع همیشه صادق نیست. برخلاف آزمون t مستقل، آزمون Mann-Whitney U به شما این امکان را می دهد که بسته به فرضیاتی که درباره توزیع داده های خود دارید، به نتایج متفاوتی دست پیدا کنید. این نتایج می توانند از یک مقایسه کلی بین دو جمعیت تا تعیین تفاوت در میانه های گروه ها متغیر باشند. این تفاوت ها به شکل توزیع داده ها بستگی دارند که در ادامه بیشتر توضیح داده خواهد شد.

توزیع نمرات برای مردان و زنان
در دو نمودار فوق، توزیع نمرات برای “مردان” و “زنان” دارای شکل یکسانی می باشد. در نمودار سمت چپ، توزیع نمرات برای “مردان” (که در نمودار سمت راست با رنگ آبی نشان داده شده است) قابل مشاهده نیست، زیرا هر دو توزیع کاملاً یکسان هستند (به این معنا که هر دو توزیع بر روی یکدیگر قرار گرفته اند و توزیع مردان که به رنگ آبی است، زیر توزیع زنان که به رنگ قرمز است، پنهان شده است). اما در نمودار سمت راست، با وجود اینکه هر دو توزیع شکل یکسانی دارند، مکان آن ها متفاوت است (یعنی توزیع یکی از گروه های متغیر مستقل دارای مقادیر بالاتر یا پایین تر نسبت به توزیع گروه دیگر می باشد – در این مثال، مقادیر مربوط به زنان به طور کلی از مقادیر مردان بالاتر است).
هنگامی که داده های خود را تجزیه و تحلیل می کنید، بسیار بعید است که دو توزیع شما کاملاً یکسان باشند، اما ممکن است دارای شکل یکسان (یا “مشابه”) باشند. اگر چنین باشد، می توانید از نرم افزار SPSS Statistics برای انجام آزمون Mann-Whitney U جهت مقایسه میانه های متغیر وابسته (مانند نمره مشارکت) برای دو گروه (مثلاً مردان و زنان) در متغیر مستقل مورد نظر (مانند جنسیت) استفاده کنید. اما اگر دو توزیع دارای شکل متفاوتی باشند، تنها می توانید از آزمون Mann-Whitney U برای مقایسه میانگین رتبه ها استفاده کنید.
بنابراین، هنگام انجام آزمون Mann-Whitney U، لازم است که از SPSS Statistics برای تعیین اینکه آیا دو توزیع دارای شکل یکسان یا متفاوتی هستند، استفاده کنید. این کار نیاز به چند مرحله اضافی در SPSS دارد، اما یک فرآیند گامبهگام ساده است که در راهنمای پیشرفته آزمون Mann-Whitney U توضیح داده شده است. در این راهنمای “شروع سریع”، نحوه اجرای آزمون Mann-Whitney U را در شرایطی که دو توزیع دارای شکل مشابه نیستند (به طوری که تنها می توان میانگین رتبه ها را مقایسه کرد و نه میانه ها) آموزش خواهیم داد.
از آزمون Mann-Whitney U چه زمانی استفاده می شود؟
آزمون Mann-Whitney U یک آزمون ناپارامتریک است که برای مقایسه دو گروه مستقل به کار می رود. این آزمون زمانی استفاده می شود که داده های دو گروه دارای توزیع نرمال نباشند یا اندازه نمونه ها کوچک باشد و نتوان فرض نرمال بودن را تأیید کرد. در واقع، آزمون Mann-Whitney U جایگزینی برای آزمون t مستقل محسوب می شود، اما بر خلاف آن، نیازی به فرض نرمال بودن داده ها ندارد. به جای مقایسه میانگین ها، این آزمون بر رتبه های داده ها تمرکز می کند و بررسی می کند که آیا یک گروه به طور سیستماتیک مقادیر بیشتری نسبت به گروه دیگر دارد یا خیر.
این آزمون در شرایط مختلفی کاربرد دارد، از جمله در پژوهش های علوم اجتماعی، پزشکی و اقتصاد که داده ها اغلب دارای توزیع نامشخص یا دارای داده های پرت هستند. به دلیل عدم نیاز به فرض های سختگیرانه، آزمون Mann-Whitney U به عنوان روشی انعطاف پذیر برای تحلیل داده های غیر نرمال و رتبه ای شناخته می شود. همچنین، این آزمون برای داده هایی که دارای مقیاس ترتیبی هستند نیز مناسب است، زیرا به جای استفاده از میانگین و انحراف معیار، بر اساس رتبه بندی مقادیر انجام می شود.
کاربردهای آزمون Mann-Whitney U:
- مقایسه دو گروه مستقل زمانی که داده ها توزیع نرمال ندارند.
- تحلیل داده های با مقیاس ترتیبی که میانگین آنها معنا ندارد.
- زمانی که تعداد نمونه ها کم است و استفاده از آزمون های پارامتریک مناسب نمی باشد.
- بررسی تأثیر یک مداخله در دو گروه آزمایش و کنترل بدون فرض نرمال بودن داده ها.
- تحلیل داده های پزشکی، علوم اجتماعی و روانشناسی که اغلب دارای توزیع نامشخص هستند.
- زمانی که داده ها دارای مقادیر پرت باشند و بر نتایج آزمون های پارامتریک تأثیر بگذارند.
- جایگزین آزمون t مستقل در شرایطی که فرض نرمال بودن برقرار نیست.
تفاوت توزیع نرمال و توزیع چوله
در این نوع توزیع، داده ها به صورت متقارن پیرامون میانگین توزیع شده اند و نمودار آن شکلی زنگولهای دارد. در یک توزیع نرمال، میانگین، میانه و مد (نما) برابر هستند. این نوع توزیع برای بسیاری از آزمون های آماری پارامتریک، مانند آزمون t، ضروری است.
زمانی که داده ها به طور نامتقارن توزیع شده باشند، توزیع چوله رخ می دهد. چولگی می تواند به سمت راست (چوله به راست) یا به سمت چپ (چوله به چپ) باشد. در این شرایط، میانگین، میانه و مد مقادیر متفاوتی خواهند داشت. از آنجایی که بسیاری از آزمون های پارامتریک به فرض نرمال بودن داده ها وابسته هستند، در صورت چولگی داده ها، باید از آزمون های ناپارامتریک مانند Mann-Whitney U استفاده کرد.
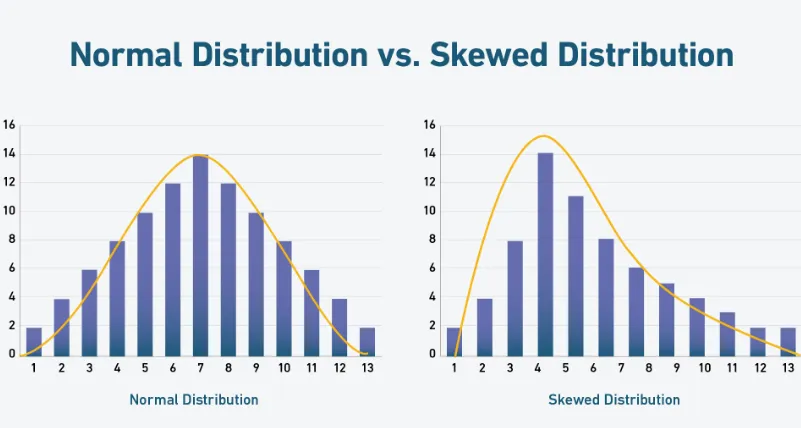
توزیع Normal در مقابل توزیع Skewed
مفروضات آزمون Mann Whitney U
هر روش آماری دارای مفروضاتی است. مفروضات به این معنا هستند که داده های شما باید دارای ویژگی های خاصی باشند تا نتایج روش آماری دقیق و معتبر باشند.
مفروضات این آزمون شامل موارد زیر می باشند:
- پیوستگی داده ها
- توزیع چوله (Skewed Distribution)
- نمونه گیری تصادفی
- کافی بودن حجم داده ها
- شکل مشابه بین گروه ها
در ادامه، هر یک از این مفروضات را به طور جداگانه بررسی می کنیم.
1. پیوستگی داده ها
متغیری که قصد دارید بین دو گروه مقایسه کنید، باید یک متغیر پیوسته باشد. متغیر پیوسته به این معناست که می تواند هر مقدار معقولی را بپذیرد.
نمونه هایی از متغیرهای پیوسته: سن، وزن، قد، نمرات آزمون، امتیازات نظرسنجی، حقوق سالانه و غیره.
اگر متغیری که بررسی می کنید به صورت یک نسبت بیان شود (مثلاً “۴۸٪ از مردان رأی دادند در مقابل ۵۶٪ از زنان”)، احتمالاً بهتر است از آزمون Z دو نسبت (Two Proportion Z-Test) استفاده کنید.
2. توزیع چوله (Skewed Distribution)
متغیری که بررسی می کنید نیازی به توزیع نرمال (به شکل زنگولهای) ندارد. در آمار، توزیع نرمال به معنای داشتن یک توزیع به شکل منحنی زنگولهای می باشد.
از آزمون Mann-Whitney U می توان در شرایطی که داده های متغیر مورد بررسی دارای توزیع چوله هستند و نه توزیع نرمال، استفاده کرد. این ویژگی باعث می شود که آزمون Mann-Whitney U برای بسیاری از داده های واقعی که اغلب دارای چولگی هستند، مناسب باشد.

توزیع نرمال که شکل زنگولهای دارد و بیشتر دادهها در میانه توزیع قرار گرفتهاند.

توزیع چوله، دادهها به طور نامتقارن توزیع شده باشند و بیشتر دادهها در یک سمت قرار بگیرند.
3. نمونه گیری تصادفی
نقاط داده برای هر گروه در تحلیل شما باید از یک نمونه تصادفی ساده انتخاب شده باشند. این بدین معناست که اگر بخواهید بررسی کنید که آیا نوشیدن نوشابه های شیرین باعث افزایش وزن میشود، باید ابتدا گروهی از افرادی که نوشابه مینوشند را به طور تصادفی انتخاب کنید و سپس گروهی از افرادی که نوشابه نمینوشند را به طور تصادفی برای گروه “غیر نوشابهخور ها” انتخاب کنید.
نکته مهم این است که نقاط داده برای هر گروه به طور تصادفی انتخاب شده اند. این امر حائز اهمیت است زیرا اگر گروه های شما به صورت تصادفی انتخاب نشده باشند، تحلیل شما نادرست خواهد بود. در اصطلاح آماری، به این حالت تعصب (bias) گفته میشود، که به تمایل به داشتن نتایج نادرست به دلیل داده های ضعیف یا انتخابی اشاره دارد.
4. حجم داده کافی
حجم نمونه (یا اندازه مجموعه داده) باید در هر گروه بیشتر از 5 باشد. برخی افراد استدلال میکنند که باید حجم نمونه بیشتر از این مقدار باشد، اما معمولاً داشتن بیشتر از 5 داده در هر گروه کافی است.
حجم نمونه همچنین به اندازه تفاوت مورد انتظار بین گروهها بستگی دارد. اگر انتظار دارید تفاوت زیادی بین گروه ها وجود داشته باشد، میتوانید با حجم نمونه کوچکتر هم به نتایج معناداری برسید. اما اگر انتظار دارید تفاوت کمی بین گروه ها وجود داشته باشد، احتمالاً نیاز به حجم نمونه بزرگتری دارید.
5. شکل مشابه بین گروه ها
برای اینکه بتوانید بگویید دو گروه شما از نظر میانگین (یا میانه در این مورد) متفاوت هستند، باید گروه های شما از نظر شکل در هنگام رسم نمودار هیستوگرام مشابه باشند. اگر این دو گروه شکل مشابهی داشته باشند، می توانید بگویید که میانه ها (یا میانگین ها) متفاوت هستند، اگر آزمون Mann Whitney U معنادار باشد.
اگر دو گروه شما شکل مشابهی نداشته باشند، می توانید در نتایج خود از تفاوت بین گروه ها صحبت کنید، اما نمیتوانید تفاوت در مقدار میانگین (یا میانه) را استدلال کنید.
مثال آزمون Mann Whitney U
- گروه 1: درمان پزشکی آزمایشی را دریافت کردهاند.
- گروه 2: پلاسیبو یا شرایط کنترل را دریافت کردهاند.
- متغیر مورد نظر: زمان بهبودی از بیماری بر حسب روز.
در این مثال، گروه 1 گروه درمان ما است زیرا درمان پزشکی آزمایشی را دریافت کرده اند. گروه 2 گروه کنترل است زیرا شرایط کنترل را دریافت کرده اند.
فرضیه صفر، که در اصطلاح آماری به معنای آنچه اتفاق میافتد اگر درمان هیچ تاثیری نداشته باشد، این است که گروه 1 و گروه 2 به طور میانگین در حدود زمان مشابهی از بیماری بهبود می یابند. هدف ما این است که تعیین کنیم آیا دریافت درمان پزشکی آزمایشی باعث کاهش تعداد روزهایی که بیماران برای بهبودی از بیماری نیاز دارند، می شود یا نه.
در حین انجام آزمایش، زمان بهبودی هر بیمار از بیماری را ردیابی می کنیم. معمولاً از آزمون Mann-Whitney U زمانی استفاده میکنیم که متغیر مورد نظر ما چوله باشد، به این معنا که توزیع نرمال ندارد (چوله بودن به معنای متمایل بودن به سمت چپ یا راست با بیشتر دادهها در لبه توزیع است). در این مورد، زمان بهبودی از بیماری برای هر دو گروه چوله است.
پس از پایان آزمایش، گروه های دوگانه را با استفاده از آزمون Mann-Whitney U بر اساس متغیر مورد نظر خود (زمان بهبودی کامل) مقایسه می کنیم. وقتی تحلیل را انجام میدهیم، یک آماره W و یک مقدار p به دست میآوریم.
آماره W اندازه گیری است برای اینکه چقدر گروه ها در متغیر بهبودی از یکدیگر متفاوت هستند. مقدار p احتمال مشاهده نتایج ما را فرض می کند که درمان هیچ تاثیری ندارد. مقدار p کمتر از یا برابر با ۰.۰۵ به این معناست که نتیجه ما معنادار است و می توانیم اعتماد کنیم که تفاوت به طور تصادفی به وجود نیامده است.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











