توزیع نرمال چیست؟ خواص، کاربردها و فرمول
چکیده مقاله :
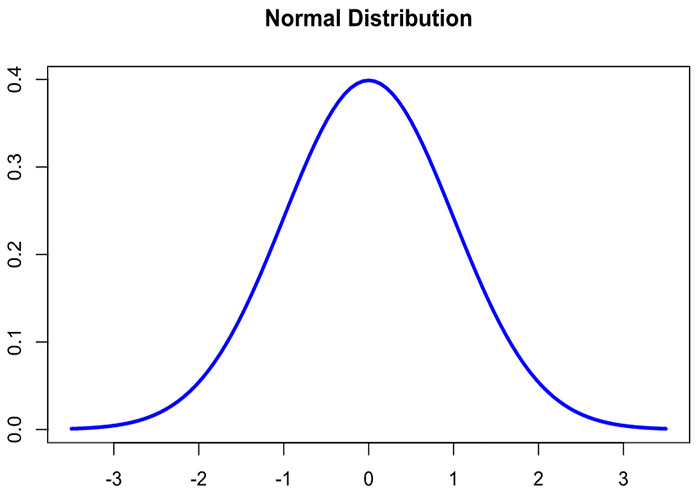
توزیع نرمال که با نام توزیع گاوسی نیز شناخته می شود، مهمترین توزیع احتمال در آمار برای متغیرهای تصادفی مستقل است. اکثر مردم منحنی زنگشکل آشنا آن را در گزارشهای آماری تشخیص میدهند. توزیع نرمال یک توزیع احتمال پیوسته است که حول میانگین آن متقارن است، بیشتر مشاهدات در اطراف قله مرکزی جمع می شوند و احتمالات برای مقادیر دورتر از میانگین به طور مساوی در هر دو جهت کاهش می یابد. مقادیر شدید در هر دو دنباله توزیع به طور مشابه بعید است. در حالی که Normal Distribution متقارن است، همه توزیع های متقارن نرمال نیستند. به عنوان مثال، توزیع t، کوشی و لجستیک Student متقارن هستند. در این مقاله به یکی از پرتکرار ترین نمودارها در تحلیل آماری یعنی همین نمودار توزیع نرمال و خود Normal Distribution می پردازیم. تمام سوالات خود را در رابطه با Normal Distribution چیست دریافت خواهید کرد و مفهوم آن را توضیح می دهیم. ویژگی ها و مشخصه های آن را بیان می کنیم و با ذکر چند مثال و فرمول محاسبه آن به جزئیات آن می پردازیم. همچنین تفسیر آن را با استفاده از سایر شاخص های آماری دیگر بیان می کنیم.
1- توزیع نرمال چیست ؟
توزیع نرمال نوعی توزیع احتمال پیوسته است که در آن اکثر نقاط داده به سمت وسط محدوده خوشه می شوند، در حالی که بقیه به طور متقارن به سمت هر یک از دو انتهایی کاهش می یابند. وسط محدوده به عنوان میانگین توزیع نیز شناخته می شود.
Normal Distribution، که به نام توزیع گاوسی نیز شناخته می شود، یک توزیع احتمال متقارن نسبت به میانگین است، که نشان می دهد داده های نزدیک به میانگین از نظر وقوع بیشتر از داده های دور از میانگین هستند. در شکل گرافیکی، Normal Distribution به صورت “منحنی زنگ” ظاهر می شود. به بیان دیگر توزیع نرمال به عنوان منحنی زنگ احتمال نیز شناخته می شود. نسبت به میانگین متقارن است و نشان می دهد که مقادیر نزدیک به میانگین بیشتر از مقادیر دورتر از میانگین رخ می دهد.
نکات کلیدی
- توزیع نرمال عبارت مناسب برای منحنی زنگ احتمال است.
- در توزیع نرمال میانگین صفر و انحراف معیار 1 است. دارای چولگی صفر و کشیدگی 3 است.
- توزیع های نرمال متقارن هستند، اما همه توزیع های متقارن نرمال نیستند.
- بسیاری از پدیده های طبیعی به Normal Distribution نزدیک می شوند.
- در امور مالی، اکثر توزیعهای قیمتگذاری کاملاً نرمال نیستند.
جهت آشنایی بیشتر می توانید مقاله زیر را با عنوان تحلیل آماری چیست مطالعه نمایید.
از نظر گرافیکی، یک Normal Distribution به دلیل شکل آن یک منحنی زنگی است. شکل دقیق می تواند با توجه به توزیع مقادیر در جمعیت متفاوت باشد. جمعیت کل مجموعه ای از نقاط داده است که بخشی از توزیع هستند.
صرف نظر از شکل دقیق آن، منحنی زنگ توزیع نرمال همیشه نسبت به میانگین متقارن است. توزیع متقارن به این معنی است که یک خط تقسیم عمودی که از طریق مقدار حداکثر/میانگین کشیده شده است، دو تصویر آینه ای در دو طرف خط ایجاد می کند که در آن نیمی از جمعیت کمتر از میانگین و نیمی بیشتر است. با این حال، عکس آن همیشه صادق نیست. یعنی همه توزیع های متقارن نرمال نیستند. در منحنی زنگ، اوج همیشه در وسط است و میانگین، مد و میانه همه یکسان هستند.
2- مفهوم توزیع نرمال
در تئوری احتمالات و آمار، Normal Distribution که توزیع گاوسی نیز نامیده می شود، مهم ترین توزیع احتمال پیوسته است. همانطورکه گفته شد، گاهی اوقات به آن منحنی زنگ نیز می گویند. تعداد زیادی از متغیرهای تصادفی تقریباً یا دقیقاً با توزیع نرمال در هر علم فیزیکی و اقتصاد نشان داده می شوند. علاوه بر این، می توان از آن برای تقریب سایر توزیع های احتمال استفاده کرد. درواقع Normal Distribution رایج ترین نوع توزیعی است که در تحلیل تکنیکال بازار سهام و سایر انواع تحلیل های آماری فرض می شود. توزیع نرمال استاندارد دو پارامتر دارد: میانگین و انحراف معیار.
مدل توزیع نرمال در آمار مهم است و برای قضیه حد مرکزی (CLT) کلیدی است. این نظریه بیان میکند که میانگینهای محاسبهشده از متغیرهای تصادفی مستقل و با توزیع یکسان، بدون توجه به نوع توزیعی که متغیرها از آن نمونهبرداری میشوند، توزیعهای تقریباً نرمال دارند (به شرطی که واریانس محدود داشته باشد).
توزیع نرمال یکی از انواع توزیع متقارن است. توزیع متقارن زمانی اتفاق می افتد که یک خط تقسیم دو تصویر آینه ای ایجاد کند. همه توزیعهای متقارن نرمال نیستند، زیرا برخی از دادهها میتوانند علاوه بر منحنی زنگی که Normal Distribution را نشان میدهد، به صورت دو قوز یا یک سری تپه ظاهر شوند.
3- نمونه های اساسی توزیع نرمال: قد و وزن
ارتفاع یک مثال ساده از مقادیری است که از الگوی توزیع نرمال پیروی می کنند. اکثر مردم قد متوسطی دارند – هر چه که برای یک جمعیت خاص باشد. اگر قد این افراد به صورت گرافیکی همراه با قد افراد بلندتر و کوتاهتر از میانگین نشان داده شود، توزیع همیشه یک Normal Distribution خواهد بود. این به این دلیل است که افراد با قد متوسط نزدیک به وسط قرار می گیرند، در حالی که آنهایی که قد بلندتر و کوتاهتر هستند دورتر خواهند بود.
علاوه بر این، این گروه های اخیر از تعداد بسیار کمی از افراد تشکیل خواهند شد. تعداد افرادی که بسیار قد بلند یا بسیار کوتاه قد هستند حتی کمتر خواهد بود، بنابراین آنها بیشترین فاصله را از میانگین دارند.
به طور مشابه، اگر میانگین وزن جمعیت مورد نظر مشخص باشد، وزن نیز می تواند از توزیع نرمال پیروی کند. مانند قد، وزنهای پرت نیز کسانی هستند که بیشتر یا کمتر از میانگین وزن دارند. هر چه انحراف از میانگین بیشتر باشد، آن نقاط داده در نمودار توزیع دورتر خواهند بود.
4- ویژگی های توزیع نرمال
توزیع نرمال دارای چندین مشخصه و ویژگی کلیدی است که آن را تعریف می کند.
اولاً، میانگین (متوسط)، میانه (نقطه میانی) و مد (متداول ترین مشاهده) همه با یکدیگر برابر هستند. علاوه بر این، این مقادیر همگی اوج یا بالاترین نقطه توزیع را نشان می دهند. سپس توزیع به طور متقارن حول میانگین میافتد که عرض آن با انحراف استاندارد تعریف میشود. تمام توزیع های نرمال را می توان تنها با دو پارامتر توصیف کرد: میانگین و انحراف استاندارد.
برخی از ویژگی های مهم توزیع نرمال در زیر ذکر شده است:
- در یک Normal Distribution، میانگین، میانه و حالت برابر هستند (یعنی میانگین = میانه = حالت).
- مساحت کل زیر منحنی باید برابر با 1 باشد.
- منحنی توزیع شده معمولی باید در مرکز متقارن باشد.
- دقیقاً نیمی از مقادیر در سمت راست مرکز و دقیقاً نیمی از مقادیر در سمت چپ مرکز قرار دارند.
- توزیع نرمال باید با میانگین و انحراف معیار تعریف شود.
- منحنی Normal Distribution باید فقط یک قله داشته باشد. (یعنی Unimodal)
- منحنی به محور x نزدیک می شود، اما هرگز لمس نمی شود، و از میانگین دورتر می شود.
1-4- قانون تجربی
برای همه توزیعهای نرمال، 2/68 درصد از مشاهدات در انحراف معیار به علاوه یا منهای یک میانگین ظاهر میشوند. 95.4٪ از مشاهدات در +/- دو انحراف استاندارد قرار می گیرند. و 99.7٪ در +/- سه انحراف استاندارد. این واقعیت گاهی اوقات به عنوان “قاعده تجربی” نامیده می شود، یک اکتشافی که توصیف می کند که بیشتر داده ها در یک توزیع نرمال کجا ظاهر می شوند.
این بدان معنی است که داده های خارج از سه انحراف استاندارد (“3-sigma”) نشان دهنده رخدادهای نادر است.
2-4- چولگی در توزیع نرمال
چولگی میزان تقارن یک توزیع را اندازه گیری می کند. توزیع نرمال متقارن و دارای چولگی صفر است.
اگر توزیع یک مجموعه داده به جای آن دارای چولگی کمتر از صفر یا چولگی منفی (چولگی چپ) باشد، دم سمت چپ توزیع طولانیتر از دنباله راست است. چولگی مثبت (کول به راست) به این معنی است که دم سمت راست توزیع طولانی تر از سمت چپ است.
3-4- کشیدگی در توزیع نرمال
Kurtosis یا کشیدگی ضخامت انتهای دم یک توزیع را در رابطه با دم یک توزیع اندازه گیری می کند. توزیع نرمال دارای کشیدگی برابر با 3.0 است.
توزیعهایی که کشش بزرگتر از 3.0 دارند، دادههای دنباله را بیشتر از انتهای Normal Distribution نشان میدهند (به عنوان مثال، پنج یا بیشتر انحراف استاندارد از میانگین). این کشیدگی بیش از حد در آمار به عنوان لپتوکورتیک شناخته می شود، اما در محاوره بیشتر به عنوان “دم چاق” شناخته می شود. وقوع این نمودار در بازارهای مالی چیزی را توصیف می کند که به عنوان ریسک دنباله شناخته می شود.
توزیعهایی با کشیدگی کم کمتر از 3.0 (platykurtic) دمهایی را نشان میدهند که عموماً نسبت به دنبالههای توزیع عادی کمتر شدید (“لاغرتر”) هستند.
قطعا این مقاله را در رابطه کشیدگی مطالعه نمایید.
5- اهمیت توزیع نرمال
توزیع نرمال به سه دلیل اصلی یکی از مهم ترین توزیع های احتمال برای متغیرهای تصادفی مستقل است.
اول، Normal Distribution، توزیع ارزشها را برای بسیاری از پدیدههای طبیعی در طیف وسیعی از حوزهها، از جمله زیستشناسی، علوم فیزیکی، ریاضیات، مالی و اقتصاد توصیف میکند. همچنین می تواند این متغیرهای تصادفی را به دقت نمایش دهد.
علاوه بر قد و وزن، توزیع های نرمال نیز برای نشان دادن بسیاری از مقادیر دیگر از جمله موارد زیر استفاده می شود:
- خطای اندازه گیری
- فشار خون
- نمرات IQ
- قیمت دارایی
- اقدام قیمت
دوم، توزیع نرمال مهم است زیرا می توان از آن برای تقریب انواع دیگر توزیع احتمال، مانند توزیع دوجمله ای، ابر هندسی، ابر هندسی معکوس (یا منفی)، دو جمله ای منفی و توزیع پواسون استفاده کرد.
سوم، توزیع نرمال ایده کلیدی پشت قضیه حد مرکزی یا CLT است که بیان میکند که میانگینهای محاسبهشده از متغیرهای تصادفی مستقل و توزیعشده یکسان دارای توزیعهای تقریباً نرمال هستند. این بدون توجه به نوع توزیعی که متغیرها از آن نمونه برداری می شوند، تا زمانی که دارای واریانس محدود باشد صادق است.
6- منحنی توزیع نرمال
متغیرهای تصادفی پس از توزیع نرمال آنهایی هستند که مقادیر آنها می تواند هر مقدار ناشناخته را در یک محدوده مشخص پیدا کند. به عنوان مثال، پیدا کردن قد دانش آموزان در مدرسه. در اینجا، توزیع می تواند هر مقداری را در نظر بگیرد، اما در محدوده مثلاً 0 تا 6 فوت محدود می شود. این محدودیت به صورت فیزیکی در جستار ما اعمال می شود.
دامنه همچنین می تواند به -∞ تا + ∞ گسترش یابد و همچنان می توانیم یک منحنی صاف پیدا کنیم. این متغیرهای تصادفی، متغیرهای پیوسته نامیده میشوند، و سپس توزیع عادی در اینجا احتمال مقداری را که در یک محدوده خاص برای یک آزمایش معین قرار دارد، ارائه میکند. همچنین از ماشین حساب توزیع نرمال برای یافتن تابع چگالی احتمال فقط با ارائه مقدار میانگین و انحراف استاندارد استفاده کنید.
7- فرمول توزیع نرمال
توزیع نرمال از فرمول زیر پیروی می کند. توجه داشته باشید که فقط مقادیر میانگین (μ) و انحراف معیار (σ) ضروری هستند.
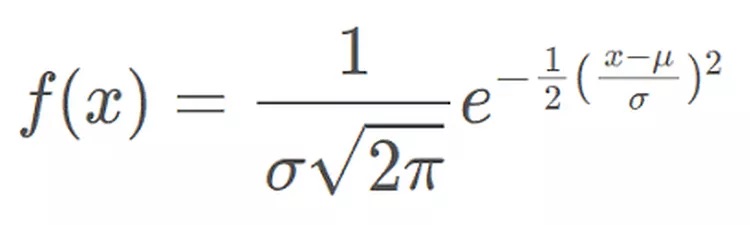
که در آن:
- x = مقدار متغیر یا داده مورد بررسی و f(x) تابع احتمال
- μ = میانگین
- σ = انحراف معیار
قاعده تجربی برای توزیعهای نرمال توضیح میدهد که بیشتر دادهها در یک توزیع نرمال کجا ظاهر میشوند و موارد زیر را بیان میکند:
- %68.2 از مشاهدات در انحراف استاندارد +/-1 از میانگین ظاهر می شوند.
- %95.4 از مشاهدات در انحراف استاندارد +/-2 قرار می گیرند. و
- %99.7 از مشاهدات در انحراف استاندارد +/-3 قرار می گیرند.
تمام نقاط داده خارج از سه انحراف استاندارد (3σ) نشان دهنده رخدادهای نادر است.
8- جدول توزیع نرمال
جدول اینجا مساحت 0 تا Z-value را نشان می دهد.
| Z-Value | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.0000 | 0.0040 | 0.0080 | 0.0120 | 0.0160 | 0.0199 | 0.0239 | 0.0279 | 0.0319 | 0.0359 |
| 0.1 | 0.0398 | 0.0438 | 0.0478 | 0.0517 | 0.0557 | 0.0596 | 0.0636 | 0.0675 | 0.0714 | 0.0753 |
| 0.2 | 0.0793 | 0.0832 | 0.0871 | 0.0910 | 0.0948 | 0.0987 | 0.1026 | 0.1064 | 0.1103 | 0.1141 |
| 0.3 | 0.1179 | 0.1217 | 0.1255 | 0.1293 | 0.1331 | 0.1368 | 0.1406 | 0.1443 | 0.1480 | 0.1517 |
| 0.4 | 0.1554 | 0.1591 | 0.1628 | 0.1664 | 0.1700 | 0.1736 | 0.1772 | 0.1808 | 0.1844 | 0.1879 |
| 0.5 | 0.1915 | 0.1950 | 0.1985 | 0.2019 | 0.2054 | 0.2088 | 0.2123 | 0.2157 | 0.2190 | 0.2224 |
| 0.6 | 0.2257 | 0.2291 | 0.2324 | 0.2357 | 0.2389 | 0.2422 | 0.2454 | 0.2486 | 0.2517 | 0.2549 |
| 0.7 | 0.2580 | 0.2611 | 0.2642 | 0.2673 | 0.2704 | 0.2734 | 0.2764 | 0.2794 | 0.2823 | 0.2852 |
| 0.8 | 0.2881 | 0.2910 | 0.2939 | 0.2967 | 0.2995 | 0.3023 | 0.3051 | 0.3078 | 0.3106 | 0.3133 |
| 0.9 | 0.3159 | 0.3186 | 0.3212 | 0.3238 | 0.3264 | 0.3289 | 0.3315 | 0.3340 | 0.3365 | 0.3389 |
| 1.0 | 0.3413 | 0.3438 | 0.3461 | 0.3485 | 0.3508 | 0.3531 | 0.3554 | 0.3577 | 0.3599 | 0.3621 |
| 1.1 | 0.3643 | 0.3665 | 0.3686 | 0.3708 | 0.3729 | 0.3749 | 0.3770 | 0.3790 | 0.3810 | 0.3830 |
| 1.2 | 0.3849 | 0.3869 | 0.3888 | 0.3907 | 0.3925 | 0.3944 | 0.3962 | 0.3980 | 0.3997 | 0.4015 |
| 1.3 | 0.4032 | 0.4049 | 0.4066 | 0.4082 | 0.4099 | 0.4115 | 0.4131 | 0.4147 | 0.4162 | 0.4177 |
| 1.4 | 0.4192 | 0.4207 | 0.4222 | 0.4236 | 0.4251 | 0.4265 | 0.4279 | 0.4292 | 0.4306 | 0.4319 |
| 1.5 | 0.4332 | 0.4345 | 0.4357 | 0.4370 | 0.4382 | 0.4394 | 0.4406 | 0.4418 | 0.4429 | 0.4441 |
| 1.6 | 0.4452 | 0.4463 | 0.4474 | 0.4484 | 0.4495 | 0.4505 | 0.4515 | 0.4525 | 0.4535 | 0.4545 |
| 1.7 | 0.4554 | 0.4564 | 0.4573 | 0.4582 | 0.4591 | 0.4599 | 0.4608 | 0.4616 | 0.4625 | 0.4633 |
| 1.8 | 0.4641 | 0.4649 | 0.4656 | 0.4664 | 0.4671 | 0.4678 | 0.4686 | 0.4693 | 0.4699 | 0.4706 |
| 1.9 | 0.4713 | 0.4719 | 0.4726 | 0.4732 | 0.4738 | 0.4744 | 0.4750 | 0.4756 | 0.4761 | 0.4767 |
| 2.0 | 0.4772 | 0.4778 | 0.4783 | 0.4788 | 0.4793 | 0.4798 | 0.4803 | 0.4808 | 0.4812 | 0.4817 |
| 2.1 | 0.4821 | 0.4826 | 0.4830 | 0.4834 | 0.4838 | 0.4842 | 0.4846 | 0.4850 | 0.4854 | 0.4857 |
| 2.2 | 0.4861 | 0.4864 | 0.4868 | 0.4871 | 0.4875 | 0.4878 | 0.4881 | 0.4884 | 0.4887 | 0.4890 |
| 2.3 | 0.4893 | 0.4896 | 0.4898 | 0.4901 | 0.4904 | 0.4906 | 0.4909 | 0.4911 | 0.4913 | 0.4916 |
| 2.4 | 0.4918 | 0.4920 | 0.4922 | 0.4925 | 0.4927 | 0.4929 | 0.4931 | 0.4932 | 0.4934 | 0.4936 |
| 2.5 | 0.4938 | 0.4940 | 0.4941 | 0.4943 | 0.4945 | 0.4946 | 0.4948 | 0.4949 | 0.4951 | 0.4952 |
| 2.6 | 0.4953 | 0.4955 | 0.4956 | 0.4957 | 0.4959 | 0.4960 | 0.4961 | 0.4962 | 0.4963 | 0.4964 |
| 2.7 | 0.4965 | 0.4966 | 0.4967 | 0.4968 | 0.4969 | 0.4970 | 0.4971 | 0.4972 | 0.4973 | 0.4974 |
| 2.8 | 0.4974 | 0.4975 | 0.4976 | 0.4977 | 0.4977 | 0.4978 | 0.4979 | 0.4979 | 0.4980 | 0.4981 |
| 2.9 | 0.4981 | 0.4982 | 0.4982 | 0.4983 | 0.4984 | 0.4984 | 0.4985 | 0.4985 | 0.4986 | 0.4986 |
| 3.0 | 0.4987 | 0.4987 | 0.4987 | 0.4988 | 0.4988 | 0.4989 | 0.4989 | 0.4989 | 0.4989 | 0.4990 |
9- پارامترهای توزیع نرمال
از آنجایی که میانگین، حالت و میانه در یک توزیع نرمال یکسان هستند، نیازی به محاسبه جداگانه آنها نیست. این مقادیر نشان دهنده بالاترین نقطه توزیع یا اوج است. سپس تمام مقادیر دیگر در توزیع به طور متقارن در اطراف میانگین قرار می گیرند. عرض میانگین با انحراف استاندارد تعریف می شود.
در واقع، تنها دو پارامتر برای توصیف یک توزیع نرمال مورد نیاز است: میانگین و انحراف استاندارد.
1. میانگین
میانگین بالاترین مقدار مرکزی منحنی زنگ است. همه مقادیر دیگر در توزیع یا در اطراف آن خوشه می شوند یا در فاصله ای از آن قرار دارند. تغییر میانگین در یک نمودار، کل منحنی را در امتداد محور x به سمت چپ یا به سمت راست تغییر می دهد. با این حال، تقارن آن همچنان حفظ خواهد شد.
2. انحراف معیار
به طور کلی، انحراف معیار معیاری برای تغییرپذیری در یک توزیع است. در یک منحنی زنگی، عرض توزیع را مشخص می کند و نشان می دهد که مقادیر دیگر چقدر از میانگین فاصله می گیرند. علاوه بر این، نشان دهنده فاصله معمولی بین میانگین و مشاهدات است.
تغییر انحراف معیار، توزیع مقادیر حول میانگین را تغییر خواهد داد. انحراف کوچکتر گسترش را کاهش می دهد – سفت کردن توزیع – در حالی که انحراف بزرگتر باعث افزایش گسترش و ایجاد توزیع گسترده تر می شود. همانطور که توزیع گسترده تر می شود، احتمال اینکه مقادیر از میانگین دورتر باشند بیشتر می شود.
10- نحوه استفاده از توزیع نرمال در امور مالی
فرض توزیع نرمال برای قیمت دارایی ها و همچنین عملکرد قیمت اعمال می شود. معامله گران ممکن است نقاط قیمت را در طول زمان ترسیم کنند تا اقدامات اخیر قیمت را در یک توزیع عادی قرار دهند. در این مورد، هر چه قیمت بیشتر از میانگین حرکت کند، احتمال اینکه دارایی بیش از حد یا کمتر ارزش گذاری شده باشد، بیشتر می شود. معامله گران می توانند از انحرافات استاندارد برای پیشنهاد معاملات احتمالی استفاده کنند. این نوع معاملات معمولاً در بازههای زمانی بسیار کوتاه انجام میشود، زیرا بازههای زمانی بزرگتر انتخاب نقاط ورودی و خروجی را بسیار سختتر میکند.
به طور مشابه، بسیاری از تئوری های آماری سعی می کنند قیمت دارایی ها را با این فرض که از توزیع نرمال پیروی می کنند، مدل کنند. در واقع، توزیعهای قیمتی تمایل به داشتن دنباله های پهن دارند و بنابراین، کشش بیش از سه دارند. حتی اگر یک دارایی دوره طولانیای را پشت سر گذاشته باشد که با Normal Distribution مطابقت داشته باشد، هیچ تضمینی وجود ندارد که عملکرد گذشته واقعاً چشماندازهای آینده را نشان دهد.
11- مثالی از توزیع نرمال
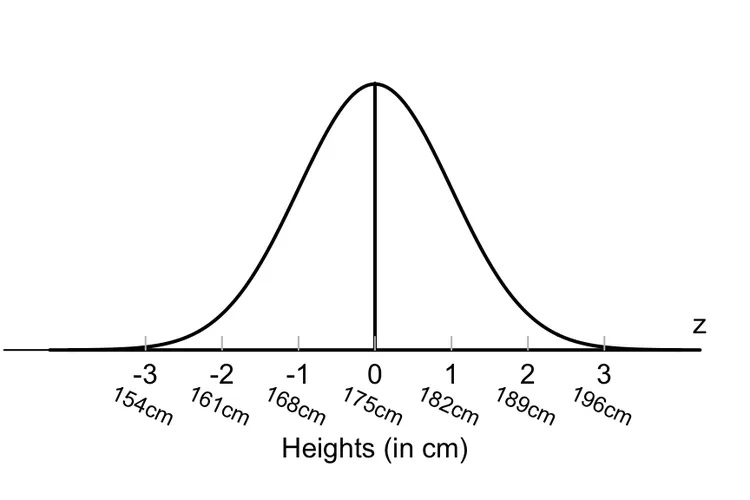
به نظر می رسد بسیاری از پدیده های طبیعی به طور نرمال توزیع شده اند. به عنوان مثال، توزیع قد انسان ها را در نظر بگیرید. میانگین قد تقریباً 175 سانتیمتر (5′ 9 اینچ) است که هم نر و هم ماده را در نظر میگیریم.
همانطور که نمودار زیر نشان می دهد، اکثر مردم با این میانگین مطابقت دارند. در این میان، افراد قد بلندتر و کوتاهتر وجود دارند، اما با کاهش فراوانی در جمعیت. طبق قانون تجربی، 99.7٪ از همه افراد با +/- سه انحراف معیار میانگین یا بین 154 سانتیمتر (5′ 0 اینچ) و 196 سانتیمتر (6′ 5 اینچ) سقوط میکنند. قد بلندتر و کوتاهتر از این بسیار نادر است (هر کدام فقط 0.15 درصد از جمعیت).
12- سوالات پرتکرار
1- منظور از توزیع نرمال چیست؟
توزیع نرمال یک نمودار متقارن از داده ها را حول مقدار میانگین آن توصیف می کند، جایی که عرض منحنی با انحراف استاندارد تعریف می شود. از نظر بصری به عنوان “منحنی زنگ” به تصویر کشیده شده است. به بیان دیگر تابع احتمالی که نحوه توزیع مقادیر یک متغیر را مشخص می کند، Normal Distribution نامیده می شود و متقارن است زیرا بیشتر مشاهدات در اطراف قله مرکزی منحنی جمع می شوند. احتمالات برای مقادیر توزیع از میانگین باریک به طور مساوی در هر دو جهت دور است.
در آمار (و در نظریه احتمال)، توزیع نرمال که توزیع گاوسی نیز نامیده می شود، مهمترین توزیع احتمال پیوسته است. گاهی اوقات به آن منحنی زنگ نیز می گویند.
2- چرا توزیع نرمال “نرمال” نامیده می شود؟
توزیع نرمال از نظر فنی به عنوان توزیع گاوسی شناخته می شود، با این حال پس از انتشارات علمی در قرن 19 که نشان می داد بسیاری از پدیده های طبیعی به نظر می رسد که به طور نرمال از میانگین انحراف دارند. اصطلاح “نرمال” را به خود گرفت. این ایده از «تغییرپذیری نرمال» به عنوان «منحنی نرمال» توسط طبیعتگرای سر فرانسیس گالتون در سال 1889 در اثرش، میراث طبیعی، رایج شد.
3- محدودیت های توزیع نرمال در امور مالی چیست؟
اگرچه توزیع نرمال یک مفهوم آماری بسیار مهم است، اما کاربردهای آن در امور مالی می تواند محدود باشد زیرا پدیده های مالی – مانند بازده مورد انتظار بازار سهام – به طور منظم در یک Normal Distribution قرار نمی گیرند. در واقع، قیمتها بیشتر از توزیع نرمال لگاریتم پیروی میکنند که دارای انحراف راست و با دم چاقتر است. بنابراین، اتکای بیش از حد به منحنی زنگ هنگام پیشبینی در مورد این رویدادها میتواند منجر به نتایج غیرقابل اعتماد شود. اگرچه اکثر تحلیلگران به خوبی از این محدودیت آگاه هستند، غلبه بر این نقص نسبتاً دشوار است زیرا اغلب مشخص نیست که از کدام توزیع آماری به عنوان جایگزین استفاده شود.
4- توزیع نرمال برای چه مواردی استفاده می شود؟
توزیع نرمال در آمار قابل توجه است و اغلب در علوم طبیعی و هنرهای اجتماعی برای توصیف متغیرهای تصادفی با ارزش واقعی که توزیع آنها ناشناخته است استفاده می شود.
5- ویژگی های یک توزیع نرمال چیست؟
ویژگی های اساسی یک توزیع نرمال عبارتند از:
- متقارن، تک وجهی (یعنی یک حالت) و مجانبی است.
- مقادیر میانگین، میانه و مد همگی برابر هستند.
- یک توزیع نرمال نسبت به مرکز آن کاملاً متقارن است. این بدان معناست که سمت چپ مرکز قله تصویر آینه ای از سمت راست است. همچنین تنها یک پیک (یعنی یک حالت) در Normal Distribution وجود دارد.
6- چگونه می دانید که داده ها به طور نرمال توزیع شده اند؟
یک هیستوگرام یک نمایش گرافیکی مفید از داده های داده شده را ارائه می دهد. هنگامی که یک هیستوگرام توزیع با منحنی نرمال آن قرار می گیرد، آنگاه توزیع به عنوان توزیع نرمال شناخته می شود.
7- چگونه از جدول توزیع نرمال استفاده می کنید؟
همانطور که می دانیم، برچسب ردیف ها شامل قسمت صحیح و اولین رقم اعشار z است. در مقابل، عنوان ستون ها دومین رقم اعشار z را تشکیل می دهد. مقادیر درون جدول، احتمالات مربوط به نوع جدول هستند. بنابراین، برای به دست آوردن مقدار 0.56 از جدول z، مقدار احتمال مربوط به سطر 0.5 و ستون 0.06 (2123/0 =) را شناسایی کنید.
مدیر2025-07-06T23:23:20+03:30جولای 6, 2025|0 Comments
چکیده مقاله: برای بهترین هوش مصنوعی برای ساخت عکس، انتخاب یک ابزار قدرتمند و خلاقانه می تواند تفاوت بزرگی در کیفیت و جذابیت تصاویر تولیدی ایجاد کند. امروزه ابزارهای متنوعی در زمینه تولید تصویر [...]
مدیر2025-07-06T14:43:33+03:30جولای 6, 2025|0 Comments
چکیده مقاله: کاربرد برنامه نویسی در مهندسی عمران نقش بسیار مهمی در افزایش دقت، سرعت و بهره وری در انجام پروژه های عمرانی ایفا می کند. با توجه به پیچیدگی تحلیل های سازه ای، [...]
مدیر2025-07-05T13:53:05+03:30جولای 5, 2025|0 Comments
چکیده مقاله: تفاوت برنامه نویسی شی گرا و ساخت یافته یکی از موضوعات مهم در درک مفاهیم پایه ای علوم کامپیوتر و طراحی نرم افزار می باشد. برنامه نویسی ساخت یافته رویکردی است که [...]
مدیر2025-07-03T23:23:36+03:30جولای 3, 2025|0 Comments
چکیده مقاله: بهترین زبان برنامه نویسی برای بازی سازی یکی از موضوعات پرطرفدار در میان علاقه مندان به دنیای گیم و توسعه نرم افزار است. انتخاب زبان مناسب نقش مهمی در موفقیت پروژه های [...]
مدیر2025-07-03T22:06:27+03:30جولای 3, 2025|0 Comments
چکیده مقاله: تفاوت برنامه نویسی سمت سرور و کلاینت یکی از مباحث اساسی در توسعه نرم افزارهای تحت وب و اپلیکیشن ها می باشد. در برنامه نویسی سمت کلاینت، کدها در مرورگر کاربر اجرا [...]
مدیر2025-07-02T13:22:19+03:30جولای 2, 2025|0 Comments
چکیده مقاله: بهترین زبان برنامه نویسی برای هوش مصنوعی موضوعی است که ذهن بسیاری از علاقه مندان به فناوری، برنامه نویسان و پژوهشگران حوزه هوش مصنوعی را به خود مشغول کرده است. با توجه [...]










با عرض سلام و احترام
بسیار کامل و عالی بود.
سپاس
سلام وقت شما بخیر
خوش حالیم که مفید واقع شده