چگونه در متلب ماتریس بنویسیم؟

چکیده مقاله:
در نرم افزار متلب (MATLAB)، یکی از پرکاربردترین ابزارها برای تحلیل داده ها و انجام محاسبات عددی، ماتریس ها هستند. این نرم افزار به صورت خاص برای کار با ماتریس ها طراحی شده و بسیاری از عملیات به صورت پیش فرض بر اساس محاسبات ماتریسی انجام می شود. یادگیری اینکه چگونه در متلب ماتریس بنویسیم، گام اول برای شروع برنامه نویسی علمی و مهندسی در این محیط است. حتی ساده ترین داده ها نیز معمولا به صورت بردار یا ماتریس وارد شده و همین ویژگی باعث می شود که متلب به ابزاری قدرتمند برای تحلیل داده های پیچیده تبدیل شود.

اگر بخواهید بدانید چگونه در متلب ماتریس بنویسیم، باید با نحوه استفاده از کروشه ها [ ] برای تعریف ماتریس ها آشنا باشید. عناصر هر سطر ماتریس با استفاده از فاصله یا کاما از هم جدا می شوند و برای تعریف سطر جدید از علامت سمی کالن (;) استفاده می شود. به عنوان مثال، برای ساخت ماتریسی با دو سطر و سه ستون می توان نوشت: [1 2 3; 4 5 6]. این ساختار ساده، پایه بسیاری از تحلیل ها و محاسبات پیچیده تر در متلب می باشد.

مقدمه: چگونه در متلب ماتریس بنویسیم؟ امروزه نحوه نوشتن ماتریس در متلب از این جهت بسیار مورد توجه قرار گرفته اسن که ماتریس یک ابزار ریاضی بسیار متنوع می باشد و از آن در حوزه های مختلفی مانند رباتیک، یادگیری ماشین، مکانیک، الکترونیک و موارد دیگر استفاده می شود.

• نرم افزار متلب چیست؟

MATLAB خود مخفف “آزمایشگاه ماتریس” (MATrix LABoratory) می باشد. تمام متغیرهای MATLAB به صورت آرایه هستند و هر متغیر می تواند شامل چندین عدد باشد. بیشتر توابع MATLAB به طور همزمان روی مقادیر متعدد عمل می کنند. در ادامه قصد داریم، به این موضوع که “چگونه در متلب ماتریس بنویسیم؟” بپردازیم و همچنین، عملیات مختلفی که می توان بر روی بردارها و ماتریس ها در MATLAB انجام داد، بررسی کنیم.

انواع بردارها و ماتریس ها

بیایید نگاهی به انواع مختلف آرایه هایی که در MATLAB استفاده می شوند، بیندازیم.

• چگونه در متلب نمودار رسم کنیم؟

1. ماتریس: یک آرایه با چندین سطر و چندین ستون می باشد.

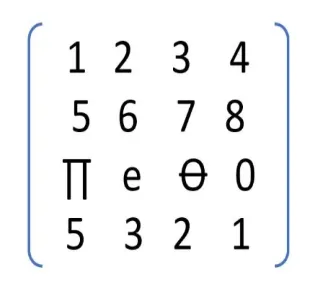
2. اسکالر: ماتریسی است که تنها یک عنصر دارد. در واقع، اسکالر یک عدد منفرد است که اساساً یک آرایه یک در یک محسوب می شود.

3. بردار ستونی: ماتریسی است که دارای یک ستون و چندین سطر می باشد.

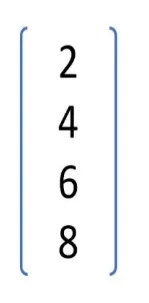
4. بردار سطری: ماتریسی است که دارای یک سطر و چندین ستون می باشد.

• حل معادله دیفرانسیل در متلب با مثال و کد

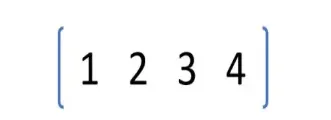
چگونه در متلب ماتریس بنویسیم؟

• ایجاد ماتریس ها به صورت دستی

می توانیم یک ماتریس یا آرایه را با استفاده از کروشه ایجاد کنیم. اگر اعداد داخل کروشه با فاصله یا ویرگول از هم جدا شوند، MATLAB  یک بردار سطری ایجاد می کند. اگر اعداد با نقطه ویرگول از هم جدا شوند، MATLAB یک بردار ستونی می سازد.

Row1 = [1 2 3 4 5] <<
Row2 = [10,20,30,40,50] <<
Col1 = [1;2;3;4;5] <<

می توان با ترکیب فضاهای خالی و نقطه ویرگول، یک ماتریس ایجاد کرد. در این روش، عناصر ماتریس به صورت سطر به سطر وارد می شوند و هر سطر با یک نقطه ویرگول از سطر بعدی جدا می گردد.

m = [1 2 3; 4 5 6; 7 8 9] <<

• پردازش تصویر با متلب

• ایجاد بردارهای با فاصله منظم

بردارهای با فاصله منظم بسیار رایج هستند و وارد کردن بردارهای طولانی به صورت دستی کار عملی نیست. MATLAB یک روش خلاصه برای ایجاد چنین بردارهایی ارائه می دهد. برای این کار، از عملگر دونقطه (:) استفاده کرده و مقدار شروع و مقدار پایان را مشخص می کنیم.

• روش نابجایی در متلب

even_row = 5 : 8 <<

این دستور یک بردار سطری شامل عناصر  5, 6, 7, 8 ایجاد می کند .به طور پیش فرض، عملگر دونقطه فاصله 1 را بین عناصر در نظر می گیرد. اما می توانیم یک فاصله دلخواه نیز مشخص کنیم.

• مقایسه متلب با پایتون

even_row = 20 : 2 : 30 <<

این دستور یک بردار سطری شامل عناصر  20, 22, 24, 26, 28, 30 ایجاد می کند.

even_row = 1 : 0.5 : 5 <<

این دستور یک بردار سطری شامل عناصر  1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0 ایجاد می کند.

• شبیه سازی بازوی ربات با متلب

• استفاده از تابع linspace()

روش دیگر برای ایجاد بردارهای با فاصله منظم، استفاده از تابع linspace()  می باشد. در این روش، تعداد عناصر مورد نظر در بردار را مشخص می کنیم.

even_row = linspace(0, 1, 5) <<

این دستور یک بردار سطری با ۵ عنصر ایجاد می کند که به طور یکنواخت از 0 تا 1  توزیع شده اند.

• شبیه سازی

• ایجاد بردارهای ستونی

تا اینجا بردارهای سطری ایجاد کردیم. اما چگونه می توان در متلب بردارهای ستونی ایجاد کرد؟ می توانیم این کار را به صورت دستی و با جدا کردن عناصر با نقطه ویرگول انجام دهیم.

col1 = [2; 4; 6; 8; 10] <<

روش دیگر این است که ابتدا یک بردار سطری را با استفاده از یکی از روش های بالا ایجاد کنیم و سپس از عملگر ترانهاده (‘) برای تبدیل آن به بردار ستونی استفاده نماییم.

even_col = even_row’ <<

• مزایا و معایب زبان برنامه نویسی متلب

ترکیب ماتریس ها در متلب

در MATLAB می توان با استفاده از کروشه  [ ] ماتریس ها را در صورتی که اندازه آن ها مطابقت داشته باشد، به یکدیگر متصل کرد.

ابتدا دو بردار سطری ایجاد می کنیم:

•  row1 با عناصر 1, 2, 3
•  row2 با عناصر 4, 5, 6

r1 = [1:3] <<
r2 = [4:6] <<
A = [r1; r2] <<

• نحوه اتصال متلب به آردوینو: مراحل، مزایا و کاربردها

ایجاد سه بردار ستونی:

col1 با عناصر 1, 4

col2 با عناصر 2, 5

col3 با عناصر 3, 6

c1 = [1; 4] <<

c2 = [2; 5] <<

c3 = [3 6]’ <<

A = [c1 c2 c3] <<

ترکیب دو ماتریس A = [1 2 3; 4 5 6]  و ماتریس B = [10 11 12; 13 14 15] به صورت افقی باعث ایجاد ماتریس c می شود.

;A= [1 2 3; 4 5 6] <<

;[10 11 12; 13 14 15]=B <<

;C = [A B] <<

• شبیه سازی با متلب

در نتیجه:

C=

1      2      3      10      11      12

4      5      6      13      14      15

این روش ماتریس  C را که یک ماتریس  2 × 6 است، ایجاد می کند.

• روش تنصیف در متلب

توابع zeros، ones و  rand() در MATLAB

• تابع zeros

این تابع ماتریسی با تمامی صفرها و با اندازه سطرها و ستون های داده شده ایجاد می کند.

• روش ژاکوبی در متلب همراه با کد، مزایا و کاربرد

مثال:

می توانید از تابع zeros  در MATLAB به شکل زیر استفاده کنید:

m0 = zeros(3,3) <<

• فرق متلب ورژن a و b چیست؟

خروجی:

m0 =

0   0   0

0   0   0

0   0   0

• تابع ones

ماتریسی که توسط این تابع ایجاد می شود، تمامی مقادیر آن یک خواهد بود.

مثال:

می توانید از تابع  ones در MATLAB به شکل زیر استفاده کنید:

m1 = ones(3,3) <<

• فرق متلب با فرترن: مزایا، کاربرد، ویژگی و نصب

خروجی:

m1 =

1   1   1

1   1   1

1   1   1

• تابع rand()

تابع  rand() به شما این امکان را می دهد که یک ماتریس با عناصر تصادفی برای اندازه داده شده ایجاد کنید.

• کد متلب گوس سایدل

مثال:

m1 = rand(3,3) <<

خروجی:

m1 =

0.8147   0.9134   0.2785

0.9058   0.6324   0.5469

0.1270   0.0975   0.9575

این تابع یک ماتریس ۳ × ۳ با مقادیر تصادفی بین ۰ و ۱ ایجاد می کند.

• لگوریتم ژنتیک در متلب

کاربرد های نوشتن ماتریس در متلب

از ماتریس ها برای رسم نمودارها، آمار و همچنین انجام مطالعات علمی و تحقیقاتی در حوزه های مختلف استفاده می شود. ماتریس ها همچنین می توانند برای نمایش داده های دنیای واقعی مانند جمعیت افراد، نرخ مرگ و میر نوزادان و غیره به کار روند. آن ها بهترین روش های نمایش برای رسم نظرسنجی ها می باشند.

• چگونه در متلب تابع تعریف کنیم؟

همچنین، ماتریس های تبدیل معمولاً در گرافیک کامپیوتری و پردازش تصویر استفاده می شوند. از ماتریس ها در تصاویر تولید شده توسط کامپیوتر که اثرات بازتاب و انحراف دارند، مانند عبور نور از آب در حال لرزش، استفاده می شود. این همان روشی است که ماتریس ها در مهندسی به کار می روند.

ماتریس ها می توانند برای حل مسائلی مانند دینامیک، معادلات حرکت و غیره استفاده شوند. همچنین برای محاسبه سرعت، شتاب، جابجایی و انحرافات توابع بسیار مؤثر هستند.