شبیه سازی مونت کارلو: کاربرد، فرمول، پیاده سازی و کد

- شبیه سازی مونت کارلو چیست؟
- چرا شبیه سازی مونت کارلو مهم است؟
- شبیه سازی مونت کارلو چگونه کار می کند؟
- شبیه سازی مونت کارلو در مقایسه با یادگیری ماشین
- اجزای شبیه سازی مونت کارلو
- شبیه سازی مونت کارلو چگونه ریسک را ارزیابی می کند؟
- ریاضیات شبیه سازی مونت کارلو
- مراحل انجام شبیه سازی مونت کارلو
- چهار مرحله در شبیه سازی مونت کارلو
- شبیه سازی مونت کارلو برای تخمین مقدار π با پایتون
- مثال: برآورد ارزش در معرض خطر (VaR) در امور مالی
- توزیع های احتمالی در شبیه سازی مونت کارلو
- کاربردهای شبیه سازی مونت کارلو
- کاربردهای شبیه سازی مونت کارلو در هوش مصنوعی
- مزایا و معایب شبیه سازی مونت کارلو
- چالش های شبیه سازی مونت کارلو
- شبیه سازی مونت کارلو چگونه در امور مالی استفاده می شود؟
- چه حرفه هایی از شبیه سازی مونت کارلو استفاده می کنند؟
چکیده مقاله :
شبیه سازی مونت کارلو که به روش مونت کارلو یا شبیهسازی احتمال چندگانه نیز معروف است، یک تکنیک ریاضی است که برای تخمین نتایج احتمالی یک رویداد نامشخص استفاده میشود. روش مونت کارلو توسط جان فون نویمان و استانیسلاو اولام در طول جنگ جهانی دوم برای بهبود تصمیم گیری در شرایط نامشخص ابداع شد. این نام از یک شهر کازینویی معروف به نام موناکو گرفته شد، زیرا عنصر شانس هسته اصلی رویکرد مدلسازی است، شبیه به بازی رولت.
از زمان معرفی، شبیهسازی مونت کارلو تأثیر ریسک را در بسیاری از سناریوهای زندگی واقعی، مانند هوش مصنوعی، قیمت سهام، پیشبینی فروش، مدیریت پروژه و قیمتگذاری ارزیابی کرده است. آنها همچنین تعدادی مزیت را نسبت به مدل های پیش بینی با ورودی های ثابت ارائه می دهند، مانند توانایی انجام تجزیه و تحلیل حساسیت یا محاسبه همبستگی ورودی ها. تجزیه و تحلیل حساسیت به تصمیم گیرندگان اجازه می دهد تا تأثیر ورودی های فردی را بر یک نتیجه مشخص ببینند و همبستگی به آنها اجازه می دهد تا روابط بین هر متغیر ورودی را درک کنند. در این مطلب به بررسی این روش ریاضی به همراه مزایا و معایب و نخوه عملکرد و همچنین محاسبه آن در 4 مرحله می پردازیم.
شبیه سازی مونت کارلو چیست؟
شبیه سازی مونت کارلو یک تکنیک محاسباتی قدرتمند است که برای تخمین رفتار سیستم های پیچیده از طریق نمونه گیری تصادفی استفاده می شود. این روش که به دلیل وابستگی به تصادف، نام خود را از کازینو مونت کارلو گرفته است، در زمینه های مختلفی مانند مالی، مهندسی و علوم برای مدل سازی عدم قطعیت و پیش بینی نتایج به کار می رود.
به بیان دیگر شبیه سازی مونت کارلو یک تکنیک ریاضی است که برای پیش بینی نتایج احتمالی رویدادهای نامطمئن استفاده می شود. برنامه های کامپیوتری از این روش برای تحلیل داده های گذشته و پیش بینی طیفی از نتایج آینده بر اساس یک اقدام مشخص بهره می برند. به عنوان مثال، اگر بخواهید فروش ماه اول یک محصول جدید را تخمین بزنید، می توانید داده های فروش تاریخی خود را به برنامه شبیه سازی مونت کارلو ارائه دهید. برنامه با در نظر گرفتن عواملی مانند شرایط عمومی بازار، قیمت محصول و بودجه تبلیغات، مقادیر مختلفی از فروش را تخمین می زند.
شبیه سازی مونت کارلو شامل تولید نمونه های تصادفی از یک توزیع احتمالی برای تقریب رفتار یک سیستم یا فرآیند است. این روش به ما امکان می دهد که نتایج رویدادهای نامطمئن را با شبیه سازی سناریوهای متعدد ممکن تخمین بزنیم.
مراحل اصلی:
- تعریف مدل: شناسایی سیستم یا فرآیندی که باید شبیه سازی شود.
- تولید نمونه های تصادفی: استفاده از نمونه گیری تصادفی برای ایجاد سناریوهای ممکن.
- ارزیابی نتایج: محاسبه نتایج بر اساس نمونه های تولید شده.
- تحلیل نتایج: تحلیل داده های شبیه سازی شده برای نتیجه گیری در مورد سیستم.
چرا شبیه سازی مونت کارلو مهم است؟
شبیه سازی مونت کارلو یک مدل احتمالی است که می تواند عنصری از عدم قطعیت یا تصادف را در پیش بینی های خود وارد کند. هنگامی که از یک مدل احتمالی برای شبیه سازی یک نتیجه استفاده می کنید، هر بار نتایج متفاوتی به دست خواهید آورد.
برای مثال، فاصله بین خانه و محل کار شما ثابت است. اما یک شبیه سازی احتمالی ممکن است زمان های مختلفی برای سفر پیش بینی کند، با در نظر گرفتن عواملی مانند ترافیک، آب و هوای بد و خرابی وسیله نقلیه.
در مقابل، روش های پیش بینی سنتی بیشتر ماهیت قطعی دارند. این روش ها پاسخ دقیقی به پیش بینی ارائه می دهند و نمی توانند عدم قطعیت را در نظر بگیرند. به عنوان مثال، ممکن است حداقل و حداکثر زمان سفر را به شما بگویند، اما این پیش بینی ها از دقت کمتری برخوردار هستند.
مزایای شبیه سازی مونت کارلو
شبیه سازی مونت کارلو چندین نتیجه احتمالی و احتمال وقوع هر یک را از یک مجموعه بزرگ از نمونه های داده تصادفی ارائه می دهد. این روش تصویری واضح تر از پیش بینی های قطعی ارائه می کند.
برای مثال، پیش بینی ریسک های مالی نیاز به تحلیل ده ها یا صدها عامل ریسک دارد. تحلیلگران مالی از شبیه سازی مونت کارلو برای ارائه احتمال وقوع هر نتیجه ممکن استفاده می کنند.
تاریخچه شبیه سازی مونت کارلو
جان فون نیومن و استانیسلاو اولام شبیه سازی مونت کارلو (یا روش مونت کارلو) را در دهه 1940 ابداع کردند. آن ها این روش را به افتخار شهر معروف قمار در موناکو، به دلیل ماهیت تصادفی مشابه بازی رولت، مونت کارلو نامگذاری کردند. زیرا شانس و نتایج تصادفی در این تکنیک مدل سازی، مانند بازی هایی نظیر رولت، تاس و ماشین های اسلات، نقشی اساسی دارند.
این تکنیک ابتدا توسط استانیسلاو اولام، ریاضیدانی که روی پروژه منهتن (تلاش مخفیانه برای ساخت اولین سلاح اتمی) کار می کرد، توسعه یافت. او ایده خود را با جان فون نویمان، یکی از همکارانش در پروژه منهتن، در میان گذاشت و این دو با همکاری یکدیگر شبیه سازی مونت کارلو را بهبود دادند.
شبیه سازی مونت کارلو چگونه کار می کند؟
اصل اساسی شبیه سازی مونت کارلو بر ارگودیسیتی استوار است. ارگودیسیتی رفتار آماری یک نقطه متحرک در یک سیستم بسته را توصیف می کند. در یک سیستم ارگودیک، نقطه متحرک در نهایت از تمامی مکان های ممکن عبور خواهد کرد. این اصل، پایه شبیه سازی مونت کارلو می باشد، جایی که کامپیوتر تعداد کافی شبیه سازی را اجرا می کند تا نتیجه نهایی ورودی های مختلف را تولید کند.
به عنوان مثال، یک تاس شش وجهی احتمال یکششم برای آمدن هر عدد خاص دارد. زمانی که تاس را شش بار پرتاب کنید، ممکن است تاس روی شش عدد مختلف نیفتد. اما اگر پرتاب را به صورت نامحدود ادامه دهید، به احتمال تئوری یکششم برای هر عدد خواهید رسید. دقت نتایج با تعداد شبیه سازی ها متناسب است. به عبارت دیگر، اجرای 10,000 شبیه سازی نتایج دقیق تری نسبت به 100 شبیه سازی تولید می کند.
شبیه سازی مونت کارلو به همین شیوه عمل می کند. این شبیه سازی از یک سیستم کامپیوتری استفاده می کند تا تعداد کافی شبیه سازی را برای تولید نتایجی که شبیه به واقعیت هستند انجام دهد. این سیستم از تولیدکننده های اعداد تصادفی برای بازسازی عدم قطعیت ذاتی پارامترهای ورودی استفاده می کند. تولیدکننده های اعداد تصادفی برنامه های کامپیوتری هستند که دنباله ای غیرقابل پیش بینی از اعداد تصادفی تولید می کنند.
شبیه سازی مونت کارلو در مقایسه با یادگیری ماشین
یادگیری ماشین (ML) یک فناوری کامپیوتری است که از نمونه های بزرگ داده های ورودی و خروجی برای آموزش نرم افزار استفاده می کند تا رابطه بین این دو را درک کند. از سوی دیگر، شبیه سازی مونت کارلو از نمونه هایی از داده های ورودی و یک مدل ریاضی شناخته شده استفاده می کند تا نتایج احتمالی را پیش بینی کند. شما می توانید از مدل های یادگیری ماشین برای آزمایش و تایید نتایج در شبیه سازی های مونت کارلو استفاده کنید.
اجزای شبیه سازی مونت کارلو
یک تحلیل مونت کارلو شامل متغیرهای ورودی، متغیرهای خروجی، و یک مدل ریاضی می باشد. سیستم کامپیوتری متغیرهای مستقل را به یک مدل ریاضی وارد می کند، آن ها را شبیه سازی می کند، و متغیرهای وابسته را تولید می کند.
متغیرهای ورودی
متغیرهای ورودی مقادیر تصادفی هستند که بر نتیجه شبیه سازی مونت کارلو تاثیر می گذارند. به عنوان مثال، کیفیت تولید و دما متغیرهای ورودی هستند که بر دوام یک گوشی هوشمند تاثیر می گذارند. شما می توانید متغیرهای ورودی را به صورت یک دامنه از نمونه های مقدار تصادفی بیان کنید تا روش های مونت کارلو بتوانند نتایج را با مقادیر ورودی تصادفی شبیه سازی کنند.
متغیر خروجی
متغیر خروجی نتیجه تحلیل مونت کارلو می باشد. برای مثال، طول عمر مورد انتظار یک دستگاه الکترونیکی یک متغیر خروجی است که مقدار آن می تواند یک زمان مانند 6 ماه یا 2 سال باشد. نرم افزار شبیه سازی مونت کارلو متغیر خروجی را در یک هیستوگرام یا نمودار نشان می دهد که نتیجه را در یک دامنه پیوسته روی محور افقی توزیع می کند.
مدل ریاضی
یک مدل ریاضی معادله ای است که رابطه بین متغیرهای خروجی و ورودی را به صورت ریاضی توصیف می کند. به عنوان مثال، مدل ریاضی برای سودآوری به صورت زیر است:
سود = درآمد − هزینه ها
نرم افزار مونت کارلو مقادیر احتمالی را بر اساس نوع توزیع احتمالی جایگزین درآمد و هزینه ها می کند. سپس شبیه سازی را تکرار می کند تا نتیجه ای با دقت بالا به دست آید. شبیه سازی مونت کارلو ممکن است ساعت ها طول بکشد، به خصوص اگر مدل ریاضی شامل تعداد زیادی متغیر تصادفی باشد.
شبیه سازی مونت کارلو چگونه ریسک را ارزیابی می کند؟
هنگامی که با عدم قطعیت قابل توجهی در پیش بینی یا برآورد مواجه می شویم، برخی روش ها متغیر نامطمئن را با یک مقدار متوسط جایگزین می کنند. اما شبیه سازی مونت کارلو به جای استفاده از یک مقدار متوسط، از مقادیر متعددی استفاده کرده و سپس نتایج را میانگین می گیرد.
شبیه سازی های مونت کارلو کاربردهای گسترده ای در زمینه هایی دارند که با متغیرهای تصادفی مواجه هستند، به ویژه در تجارت و سرمایه گذاری. این روش برای برآورد احتمال افزایش هزینه ها در پروژه های بزرگ و همچنین احتمال حرکت قیمت یک دارایی در یک جهت خاص استفاده می شود.
در صنعت مخابرات، این شبیه سازی ها برای ارزیابی عملکرد شبکه در سناریوهای مختلف به کار می روند که به آن ها کمک می کند تا شبکه های خود را بهینه سازی کنند. شرکت های بیمه از آن ها برای اندازه گیری ریسک هایی که ممکن است متحمل شوند و برای تعیین قیمت سیاست های خود استفاده می کنند. تحلیل گران سرمایه گذاری از شبیه سازی های مونت کارلو برای ارزیابی خطر نکول یک نهاد و تحلیل مشتقاتی مانند اختیار معامله بهره می برند. برنامه ریزان مالی نیز می توانند از این شبیه سازی ها برای پیش بینی احتمال کمبود بودجه یک مشتری در دوران بازنشستگی استفاده کنند.
شبیه سازی مونت کارلو علاوه بر حوزه تجارت و مالی، کاربردهای زیادی در زمینه های دیگر مانند هواشناسی، نجوم، و فیزیک نیز دارد.
امروزه شبیه سازی های مونت کارلو به طور فزاینده ای همراه با مدل های جدید هوش مصنوعی (AI) استفاده می شوند. برای مثال، همانطور که شرکت IBM در سال 2024 اشاره کرد، بسیاری از شرکت های مالی اکنون از سیستم های رایانش با عملکرد بالا برای اجرای شبیه سازی های مونت کارلو استفاده می کنند. با افزایش تعداد این شبیه سازی ها در پرتفوی های گسترده دارایی ها و ابزارهای مالی، تفسیر نتایج به طور کامل به یک چالش رو به رشد تبدیل می شود.
ریاضیات شبیه سازی مونت کارلو
ایده اصلی در شبیه سازی مونت کارلو، استفاده از نمونه گیری تصادفی برای تخمین مقدار مورد انتظار یک تابع f در یک دامنه D است.
فرمول محاسبه مقدار مورد انتظار
فرض کنید تابع f(x) و دامنه D داده شده است. مقدار مورد انتظار E[f(x)] را می توان با استفاده از فرمول زیر تخمین زد:
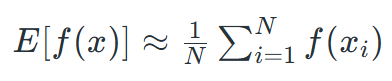
که در آن:
- N: تعداد نمونه های تصادفی.
- xi: نمونه های تصادفی که از دامنه D انتخاب شده اند.
فرمول انتگرال گیری مونت کارلو
برای تخمین انتگرال، از فرمول زیر استفاده می شود:
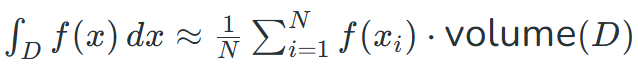
که در آن:
- volume(D): حجم دامنه D.
مراحل انجام شبیه سازی مونت کارلو
روش مونت کارلو شامل مراحل زیر می باشد:
ایجاد مدل ریاضی
یک معادله تعریف کنید که متغیرهای خروجی و ورودی را به هم متصل کند. مدل های ریاضی می توانند از فرمول های ساده کسب و کار تا معادلات پیچیده علمی متغیر باشند.
تعیین مقادیر ورودی
یکی از انواع مختلف توزیع های احتمالی را برای نمایش مقادیر ورودی انتخاب کنید. برای مثال، دمای کاری یک گوشی موبایل احتمالاً یک منحنی زنگ خواهد بود زیرا دستگاه بیشتر اوقات در دمای اتاق کار می کند.
ایجاد یک مجموعه داده نمونه
یک مجموعه داده بزرگ از نمونه های تصادفی بر اساس توزیع احتمالی انتخاب شده ایجاد کنید. اندازه نمونه باید در محدوده 100,000 باشد تا نتایج دقیقی تولید کند.
تنظیم نرم افزار شبیه سازی مونت کارلو
از نمونه های ورودی و مدل ریاضی برای پیکربندی و اجرای نرم افزار شبیه سازی مونت کارلو استفاده کنید. زمان نتایج می تواند بسته به تعداد متغیرهای ورودی متفاوت باشد و ممکن است نیاز به انتظار برای نتایج داشته باشید.
تحلیل نتایج
نتایج شبیه سازی شده را بررسی کنید تا نحوه توزیع خروجی را روی هیستوگرام مشاهده کنید. از ابزارهای آماری برای محاسبه پارامترهایی مانند مقدار میانگین، انحراف استاندارد و واریانس استفاده کنید تا مشخص کنید آیا نتیجه در محدوده انتظار شما قرار دارد یا خیر.
چهار مرحله در شبیه سازی مونت کارلو
برای انجام شبیه سازی مونت کارلو، چهار مرحله اصلی وجود دارد. به عنوان مثال، می توان از مایکروسافت اکسل یا برنامه مشابهی برای ایجاد یک شبیه سازی مونت کارلو استفاده کرد که حرکت احتمالی قیمت سهام یا دارایی های دیگر را تخمین بزند.
حرکت قیمت یک دارایی دو مؤلفه دارد:
- رانش (Drift): حرکت جهت دار مداوم قیمت.
- ورودی تصادفی: نمایانگر نوسانات بازار.
با تحلیل داده های تاریخی قیمت، می توان رانش، انحراف معیار، واریانس، و میانگین حرکت قیمت یک دارایی را تعیین کرد. این موارد اساس شبیه سازی مونت کارلو را تشکیل می دهند.
مرحله 1:
برای پیش بینی یک مسیر احتمالی قیمت، از داده های تاریخی قیمت دارایی استفاده کرده و مجموعه ای از بازده های روزانه دوره ای را با استفاده از لگاریتم طبیعی ایجاد کنید. فرمول بازده روزانه دوره ای به صورت زیر است:
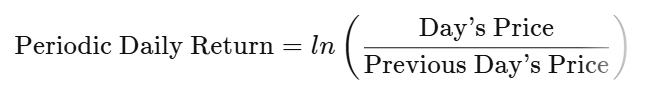
مرحله 2:
سپس از توابع AVERAGE، STDEV.P، و VAR.P در اکسل برای کل سری داده های بازده به دست آمده استفاده کنید تا ورودی های میانگین بازده روزانه، انحراف معیار، و واریانس را به ترتیب محاسبه کنید. رانش برابر است با:
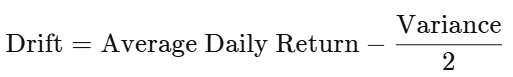
میانگین بازده روزانه: با استفاده از تابع AVERAGE از سری بازده های روزانه محاسبه می شود.
واریانس: با استفاده از تابع VAR.P از سری بازده های روزانه محاسبه می شود.
در برخی موارد، رانش می تواند برابر صفر فرض شود که این انتخاب به دیدگاه نظری خاصی بستگی دارد، اما تفاوت زیادی ایجاد نمی کند، به خصوص برای بازه های زمانی کوتاه.
مرحله 3:
سپس یک ورودی تصادفی محاسبه کنید:
مقدار تصادفی = انحراف معیار × NORMSINV(RAND())
انحراف معیار: از تابع STDEV.P در اکسل برای سری بازده های روزانه محاسبه می شود.
NORMSINV و RAND: توابع اکسل برای تولید مقادیر تصادفی هستند.
فرمول قیمت روز بعد به صورت زیر است:
قیمت روز بعد = قیمت امروز × e^(رانش + مقدار تصادفی)
مرحله 4:
برای محاسبه e به توان x در اکسل، از تابع EXP(x) استفاده کنید. این محاسبه را به تعداد دلخواه تکرار کنید (هر تکرار نمایانگر یک روز است). نتیجه، شبیه سازی حرکت آتی قیمت دارایی است.
با تولید تعداد زیادی شبیه سازی، می توانید احتمال اینکه قیمت یک دارایی مسیر مشخصی را دنبال کند، ارزیابی کنید.
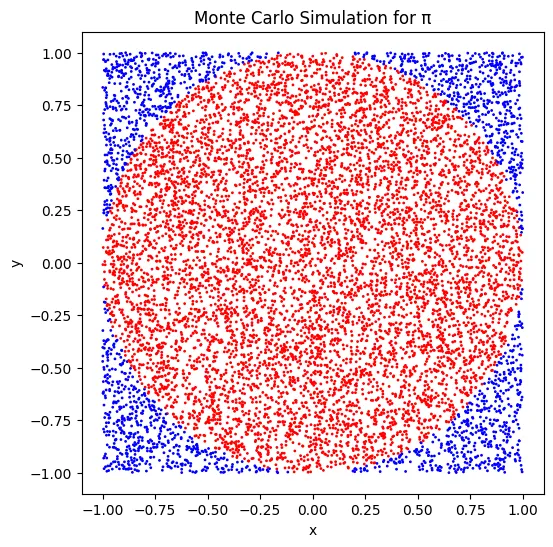
شبیه سازی مونت کارلو برای تخمین مقدار π با پایتون
برای تخمین مقدار π با استفاده از شبیه سازی مونت کارلو، از روش کلاسیک تولید نقاط تصادفی در یک مربع واحد و بررسی تعداد نقاط داخل یک ربع دایره استفاده می کنیم. مراحل این فرآیند به شرح زیر است:
- تولید نقاط تصادفی: مختصات x و y به صورت تصادفی در محدوده مربع واحد تولید می شوند.
- محاسبه فاصله: فاصله هر نقطه از مبدأ (نقطه صفر) محاسبه می شود.
- شمارش نقاط داخل دایره: تعداد نقاطی که داخل ربع دایره قرار می گیرند مشخص می شود.
- تخمین π: نسبت نقاط داخل دایره به کل نقاط تولید شده برای تخمین مقدار π استفاده می شود.
خروجی
مثال: برآورد ارزش در معرض خطر (VaR) در امور مالی
ارزش در معرض خطر (VaR) یک ابزار مدیریت ریسک است که برای تخمین زیان احتمالی ارزش دارایی یا پرتفوی در یک دوره زمانی مشخص با سطح اطمینان معین استفاده می شود. شبیه سازی مونت کارلو می تواند برای تخمین VaR با شبیه سازی ارزش آتی یک دارایی یا پورتفولیو استفاده شود.
خروجی
در سطح اطمینان 95%، مقدار ریسک در معرض (VaR) برابر با -0.0400 یا -4.00% است. این بدان معناست که احتمال 5% وجود دارد که پرتفوی بیش از 4.00% از ارزش خود را در یک دوره مشخص از دست بدهد. به عبارت دیگر، در 95 مورد از 100 سناریوی مشابه، انتظار می رود که پرتفوی کمتر از 4.00% ضرر کند.
سطح اطمینان نشان دهنده احتمال این است که ضرر واقعی از مقدار تخمین زده شده VaR بیشتر نخواهد شد. در سطح اطمینان 95%، احتمال 95% وجود دارد که ضرر برابر یا کمتر از مقدار VaR باشد و احتمال 5% وجود دارد که ضرر بیشتر از آن باشد.
مقدار تخمینی VaR برابر با -4.00% نشان می دهد که بر اساس بازده شبیه سازی شده و سطح اطمینان مشخص شده، بیشترین ضرر پیش بینی شده (یا ریسک) معادل 4.00% از ارزش پرتفوی است. این معیار به درک ریسک احتمالی ضررهای بزرگ کمک می کند و تصمیم گیری آگاهانه برای مدیریت و کاهش ریسک های مالی را ممکن می سازد.
توزیع های احتمالی در شبیه سازی مونت کارلو
توزیع های احتمالی توابع آماری هستند که یک دامنه از مقادیر توزیع شده بین حدهای مشخصی را نمایش می دهند. متخصصان آمار از توزیع های احتمالی برای پیش بینی احتمال وقوع یک متغیر نامطمئن استفاده می کنند، که ممکن است شامل مقادیر گسسته یا پیوسته باشد.
توزیع احتمالی گسسته با اعداد صحیح یا یک دنباله از اعداد محدود نمایش داده می شود. هر یک از مقادیر گسسته دارای احتمالی بزرگتر از صفر هستند. آماردان ها توزیع احتمالی گسسته را روی یک جدول رسم می کنند، اما توزیع احتمالی پیوسته به صورت یک منحنی بین دو نقطه مشخص روی محور افقی نمودار نمایش داده می شود. در زیر، برخی از انواع رایج توزیع های احتمالی که شبیه سازی مونت کارلو می تواند مدل سازی کند آورده شده است:
توزیع نرمال
توزیع نرمال که با عنوان منحنی زنگوله ای نیز شناخته می شود، به شکل متقارن شبیه زنگ است و بیشتر رویدادهای دنیای واقعی را نشان می دهد. احتمال وقوع یک مقدار تصادفی در میانه بالا است و این احتمال به طور قابل توجهی به سمت دو انتهای منحنی زنگ کاهش می یابد. به عنوان مثال، نمونه برداری تصادفی مکرر از وزن دانش آموزان در یک کلاس خاص یک نمودار توزیع نرمال به شما می دهد.
توزیع یکنواخت
توزیع یکنواخت به یک نمایش آماری از متغیرهای تصادفی با احتمال برابر اشاره دارد. زمانی که این توزیع روی نمودار رسم می شود، متغیرهای یکنواخت به صورت یک خط افقی صاف در سراسر دامنه معتبر ظاهر می شوند. به عنوان مثال، توزیع یکنواخت احتمال آمدن هر وجه یک تاس را نشان می دهد.
توزیع مثلثی
توزیع مثلثی از مقادیر حداقل، حداکثر و محتمل ترین مقدار برای نمایش متغیرهای تصادفی استفاده می کند. احتمال در محتمل ترین مقدار به اوج می رسد. به عنوان مثال، شرکت ها از توزیع مثلثی برای پیش بینی حجم فروش آینده با تعیین حداقل، حداکثر، و مقدار اوج مثلث استفاده می کنند.
کاربردهای شبیه سازی مونت کارلو
کسب و کار
رهبران کسب و کار از روش های مونت کارلو برای پیش بینی سناریوهای واقع گرایانه در تصمیم گیری استفاده می کنند.
برای مثال، یک بازاریاب باید تصمیم بگیرد که آیا افزایش بودجه تبلیغاتی برای یک دوره آموزش آنلاین یوگا امکان پذیر است یا خیر.
آن ها می توانند از مدل ریاضی مونت کارلو برای تحلیل عوامل یا متغیرهای نامطمئن زیر استفاده کنند:
- هزینه اشتراک
- هزینه تبلیغات
- نرخ ثبت نام
- نرخ ماندگاری
شبیه سازی، تاثیر تغییرات این عوامل را پیش بینی می کند و نشان می دهد که آیا تصمیم مورد نظر سودآور است یا خیر.
امور مالی
تحلیلگران مالی معمولاً پیش بینی های بلندمدتی از قیمت سهام انجام می دهند و سپس به مشتریان خود استراتژی های مناسب را توصیه می کنند. در این فرآیند، آن ها باید عوامل بازار را که ممکن است باعث تغییرات شدید در ارزش سرمایه گذاری شوند، در نظر بگیرند. به همین دلیل، آن ها از شبیه سازی مونت کارلو برای پیش بینی نتایج احتمالی به منظور حمایت از استراتژی های خود استفاده می کنند.
بازی های آنلاین
صنعت بازی و شرط بندی آنلاین تحت مقررات سختگیرانه ای قرار دارد. مشتریان انتظار دارند که نرم افزار بازی منصفانه باشد و ویژگی های مشابه با نسخه فیزیکی خود را شبیه سازی کند. بنابراین، برنامه نویسان بازی از روش مونت کارلو برای شبیه سازی نتایج و اطمینان از تجربه بازی منصفانه استفاده می کنند.
مهندسی
مهندسان باید قبل از عرضه عمومی هر محصول یا سیستمی، از قابلیت اطمینان و استحکام آن اطمینان حاصل کنند. آن ها از روش های مونت کارلو برای شبیه سازی نرخ احتمالی خرابی یک محصول بر اساس متغیرهای موجود استفاده می کنند.
به عنوان مثال، مهندسان مکانیک از شبیه سازی مونت کارلو برای تخمین دوام یک موتور در شرایط مختلف استفاده می کنند.
کاربردهای شبیه سازی مونت کارلو در هوش مصنوعی
- مسائل بهینه سازی: شبیه سازی مونت کارلو می تواند پیکربندی های مختلف ابرپارامترها را بررسی کند تا تنظیمات بهینه برای مدل هایی مانند شبکه های عصبی شناسایی شود.
- یادگیری تقویتی: روش های مونت کارلو برای تخمین ارزش اقدامات مختلف در الگوریتم های یادگیری تقویتی استفاده می شوند و به یادگیری سیاست های بهینه کمک می کنند.
- تخمین عدم قطعیت: شبیه سازی مونت کارلو تاثیر عدم قطعیت در ورودی های مدل را بر پیش بینی ها کمّی سازی می کند و قابلیت اطمینان و استحکام مدل را بهبود می بخشد.
- ارزیابی ریسک: مدل های هوش مصنوعی که نتایج مالی را پیش بینی می کنند، می توانند از شبیه سازی مونت کارلو برای ارزیابی احتمال سناریوهای مختلف مالی و ریسک های مرتبط با آن ها استفاده کنند.
- ارزیابی الگوریتم ها: شبیه سازی مونت کارلو می تواند برای مقایسه اثربخشی الگوریتم های مختلف هوش مصنوعی تحت شرایط متفاوت استفاده شود.
- افزایش داده: شبیه سازی مونت کارلو می تواند مجموعه داده های مصنوعی را با مدل سازی توزیع داده ها و تولید نمونه ها ایجاد کند و به آموزش مدل ها در صورت کمبود داده های واقعی کمک کند.
- شبیه سازی سیستم های پیچیده: این روش امکان شبیه سازی تعاملات و رفتارهای پیچیده در سیستم های هوش مصنوعی را فراهم می کند و به درک عملکرد و مسائل احتمالی کمک می کند.
- استنباط بیزی: روش های مونت کارلو مانند زنجیره مارکوف مونت کارلو (MCMC) در استنباط بیزی برای تقریب توزیع های پسین و به روز رسانی باورها بر اساس داده های جدید استفاده می شوند.
- جستجوی درختی مونت کارلو (MCTS): MCTS یک الگوریتم مبتنی بر مونت کارلو است که در هوش مصنوعی برای تصمیم گیری در بازی ها و سایر مسائل تصمیم گیری متوالی استفاده می شود.
- تحلیل پیش بینی: شبیه سازی مونت کارلو در پیش بینی روندها و رفتارهای آینده از طریق شبیه سازی سناریوهای مختلف و تحلیل نتایج آن ها کاربرد دارد.
مزایا و معایب شبیه سازی مونت کارلو
شبیه سازی مونت کارلو برای غلبه بر یک نقطه ضعف در روش های دیگر برآورد نتایج احتمالی ایجاد شد.
تفاوت اصلی این است که روش مونت کارلو به جای شروع با یک مقدار متوسط، تعداد زیادی از متغیرهای تصادفی را آزمایش کرده و سپس آن ها را میانگین می گیرد.
مانند هر شبیه سازی مالی دیگری، روش مونت کارلو بر داده های تاریخی قیمت به عنوان پایه ای برای پیش بینی داده های آینده متکی است. این روش با افزودن متغیرهای تصادفی (که توسط اعداد نمایان می شوند) الگو را مختل می کند و در نهایت این اعداد را میانگین می گیرد تا میزان ریسکی که الگو در دنیای واقعی مختل می شود، تخمین بزند.
البته هیچ شبیه سازی نمی تواند یک نتیجه قطعی را دقیقاً مشخص کند. هدف روش مونت کارلو ارائه برآورد دقیق تری از احتمال انحراف نتیجه از پیش بینی است.
چالش های شبیه سازی مونت کارلو
در هنگام استفاده از شبیه سازی مونت کارلو، دو چالش رایج وجود دارد:
- شبیه سازی مونت کارلو به شدت به مقادیر ورودی و توزیع آن ها وابسته است. اگر در انتخاب ورودی ها و توزیع احتمالی اشتباهی صورت گیرد، ممکن است نتایج نادرستی به دست آید.
- انجام آزمایش های مونت کارلو ممکن است به قدرت محاسباتی زیادی نیاز داشته باشد. محاسبات با روش مونت کارلو ممکن است ساعت ها یا حتی روزها روی یک کامپیوتر واحد طول بکشد.
شبیه سازی مونت کارلو چگونه در امور مالی استفاده می شود؟
شبیه سازی مونت کارلو برای تخمین احتمال وقوع یک نتیجه خاص استفاده می شود. به همین دلیل، این روش به طور گسترده توسط سرمایه گذاران و تحلیل گران مالی برای ارزیابی موفقیت احتمالی سرمایه گذاری های مورد نظر آن ها به کار می رود. برخی از کاربردهای رایج عبارتند از:
1. قیمت گذاری اختیار معامله:
حرکات احتمالی قیمت دارایی پایه با در نظر گرفتن هر متغیر ممکن ردیابی می شود. سپس نتایج میانگین گرفته شده و به قیمت فعلی دارایی تنزیل داده می شوند. این فرآیند به منظور نمایش بازده احتمالی اختیار معامله انجام می شود.
2. ارزش گذاری پرتفوی:
با استفاده از شبیه سازی مونت کارلو، می توان تعداد زیادی پرتفوی جایگزین را آزمایش کرد تا معیاری از ریسک نسبی آن ها به دست آید.
3. سرمایه گذاری های درآمد ثابت:
در این مورد، نرخ کوتاه مدت متغیر تصادفی است. شبیه سازی برای محاسبه تأثیر احتمالی تغییرات نرخ کوتاه مدت بر سرمایه گذاری های درآمد ثابت مانند اوراق قرضه به کار می رود.
چه حرفه هایی از شبیه سازی مونت کارلو استفاده می کنند؟
شاید بیشتر به خاطر کاربردهای مالی اش شناخته شده باشد، اما شبیه سازی مونت کارلو تقریباً در هر حرفه ای استفاده می شود که باید ریسک ها را اندازه گیری کرده و برای مقابله با آنها آماده شود.
به عنوان مثال، یک مخابرات ممکن است شبکه خود را بسازد تا تمام کاربران خود را همیشه حفظ کند. برای انجام این کار، باید تمام تغییرات احتمالی در تقاضا برای خدمات را در نظر بگیرد. باید تعیین کند که آیا سیستم در برابر فشار ساعات اوج بار و فصول اوج تحمل خواهد کرد یا خیر.
شبیهسازی مونت کارلو ممکن است به شرکت مخابراتی کمک کند تا تصمیم بگیرد که آیا خدماتش احتمالاً در برابر فشار یکشنبه Super Bowl و همچنین یکشنبههای متوسط در ماه آگوست مقاومت میکند یا خیر.
جمع بندی
شبیه سازی مونت کارلو طیفی از نتایج احتمالی را برای یک سناریوی نامشخص نشان می دهد. این تکنیک مقادیر متعددی را به متغیرهای نامشخص اختصاص می دهد، چندین نتیجه را به دست می آورد و سپس میانگین این نتایج را برای رسیدن به یک تخمین می گیرد.
از سرمایه گذاری تا مهندسی، روش مونت کارلو در بسیاری از کاربردها برای اندازه گیری ریسک از جمله تخمین احتمال سود یا زیان در یک سرمایه گذاری، یا احتمال اینکه یک پروژه بیش از بودجه اجرا شود، استفاده می شود.
مدیر2025-11-23T23:33:51+03:30نوامبر 23, 2025|0 Comments
هوش مصنوعی Grok یکی از جدیدترین و پیشرفته ترین ابزارهای هوش مصنوعی است که تجربه گفتگویی طبیعی و هوشمند را برای کاربران فراهم می کند. این سیستم نه تنها پاسخگوی سوالات روزمره است، بلکه [...]
مدیر2025-11-18T00:15:22+03:30نوامبر 18, 2025|0 Comments
هوش مصنوعی Gemini چیست؟ این سوال این روزها به یکی از پرجستجوترین موضوعات در فضای تکنولوژی تبدیل شده است، چون Gemini به عنوان پیشرفته ترین مدل هوش مصنوعی گوگل توانسته مرزهای پردازش زبان، تصویر، [...]
مدیر2025-11-07T00:34:24+03:30نوامبر 7, 2025|0 Comments
چکیده مقاله: E-E-A-T مخفف چهار واژهی Experience (تجربه)، Expertise (تخصص)، Authoritativeness (اعتبار) و Trustworthiness (قابلاعتماد بودن) است. این مفهوم توسط گوگل معرفی شده تا معیارهایی برای ارزیابی کیفیت محتوای وب سایت ها ارائه دهد. [...]
مدیر2025-11-06T00:58:39+03:30نوامبر 6, 2025|0 Comments
چکیده مقاله: GEO کلاه سیاه معبری است به دنیایی که وسوسه موفقیت سریع را با تکنیک های پرخطر همزمان می کند؛ روش هایی که تحت عناوین Black Hat GEO شناخته می شوند و شامل [...]
مدیر2025-11-24T00:05:59+03:30اکتبر 29, 2025|0 Comments
چکیده مقاله: دنیای دیجیتال هر روز در حال تغییر است و کاربران دیگر مثل گذشته به دنبال کلیک روی ده ها لینک نیستند. آن ها پاسخ را می خواهند، آن هم سریع، دقیق و [...]
مدیر2025-11-24T00:03:50+03:30اکتبر 28, 2025|0 Comments
چکیده مقاله: بهینه سازی موتور مولد (GEO) یکی از رویکردهای نوین در حوزه بهبود عملکرد سیستم های تولید محتوا و مدل های زبانی است که با هدف افزایش کیفیت، دقت و کارایی خروجی های [...]











