توزیع پواسون چیست؟ تعریف، مفهوم در آمار، فرمول و مثال

چکیده مقاله :
توزیع پواسون یک توزیع احتمال گسسته است. این احتمال را می دهد که یک رویداد تعداد معینی بار (k) در یک بازه زمانی یا مکانی مشخص رخ دهد. این توزیع تنها یک پارامتر دارد، λ ، میانگین تعداد رویدادها است. در این محتوا قصد داریم آن را به طور کامل توضیح داده و تعریف و مفهوم آن را در مسائل آماری بررسی کرده و فرمول محاسبه آن را نیز با حل چند مثال مورد ارزیابی قرار دهیم
1- توزیع پواسون چیست؟
در آمار، توزیع پواسون یک توزیع احتمال است که برای نشان دادن چند بار احتمال وقوع یک رویداد در یک دوره مشخص استفاده می شود. به عبارت دیگر، توزیع شمارشی است. Poisson Distribution اغلب برای درک رویدادهای مستقلی که در یک بازه زمانی معین با نرخ ثابتی رخ می دهند، استفاده می شود. این نام به افتخار ریاضیدان فرانسوی سیمئون دنیس پواسون گرفته شد.
توزیع پواسون یک تابع گسسته است، به این معنی که متغیر فقط می تواند مقادیر خاصی را در یک لیست (بالقوه نامحدود) بگیرد. به عبارت دیگر، متغیر نمی تواند همه مقادیر را در هر محدوده پیوسته بگیرد. برای این توزیع، متغیر فقط می تواند مقادیر اعداد کامل (0، 1، 2، 3، و غیره) را بدون کسر یا اعشار بگیرد.
به بیان دیگر، توزیع پواسون یک توزیع احتمال گسسته است، به این معنی که احتمال یک نتیجه گسسته (یعنی قابل شمارش) را می دهد. برای Poisson Distribution، نتیجه گسسته تعداد دفعاتی است که یک رویداد رخ می دهد که با k نشان داده می شود.
شما می توانید از Poisson Distribution برای پیش بینی یا توضیح تعداد رویدادهایی که در یک بازه زمانی یا مکانی معین رخ می دهند استفاده کنید. “رویدادها” می تواند هر چیزی باشد، از موارد بیماری گرفته تا خرید مشتری تا برخورد شهاب سنگ. فاصله زمانی می تواند هر مقدار مشخصی از زمان یا مکان باشد، مانند 10 روز یا 5 اینچ مربع.
شما می توانید از توزیع پواسون در موارد زیر استفاده کنید:
- رویدادهای فردی به صورت تصادفی و مستقل اتفاق میافتند. یعنی احتمال یک رویداد بر احتمال رویداد دیگر تأثیر نمی گذارد.
- شما میانگین تعداد رویدادهایی را که در یک بازه زمانی یا مکانی معین رخ می دهند، می دانید. این عدد λ نامیده می شود و ثابت فرض می شود.
هنگامی که رویدادها از توزیع پواسون پیروی می کنند، λ تنها چیزی است که برای محاسبه احتمال وقوع یک رویداد در تعداد معینی بار باید بدانید.
مفاهیم کلیدی
- توزیع پواسون که به نام ریاضیدان فرانسوی سیمئون دنیس پواسون نامگذاری شده است، می تواند برای تخمین چند بار احتمال وقوع یک رویداد در بازه های زمانی “X” استفاده شود.
- توزیع پواسون زمانی استفاده می شود که متغیر مورد نظر یک متغیر شمارش گسسته باشد.
- بسیاری از دادههای اقتصادی و مالی بهعنوان متغیرهای شمارش ظاهر میشوند، مثلاً چند بار یک فرد در یک سال معین بیکار میشود، بنابراین خود را به تجزیه و تحلیل با Poisson Distribution وا میدارند.
2- مفهوم توزیع پواسون
از توزیع پواسون می توان برای تخمین اینکه چقدر احتمال دارد چیزی “X” بار اتفاق بیفتد استفاده شود. به عنوان مثال، اگر میانگین تعداد افرادی که در یک شب جمعه در یک رستوران چیزبرگر از یک رستوران زنجیرهای چیزبرگر میخرند، 200 نفر باشد، این توزیع میتواند به سؤالاتی مانند «احتمال اینکه بیش از 300 نفر این کار را انجام دهند چقدر است.» پاسخ دهد. استفاده از Poisson Distribution بدین ترتیب مدیران را قادر می سازد تا سیستم های زمان بندی بهینه ای را معرفی کنند که مثلاً با یک توزیع نرمال کار نمی کنند.
یکی از معروفترین کاربردهای تاریخی و عملی توزیع پواسون، تخمین تعداد سالانه سربازان سواره نظام پروس بود که در اثر ضربههای اسب کشته میشدند. نمونه های مدرن شامل تخمین تعداد تصادفات اتومبیل در یک شهر با اندازه معین است. در فیزیولوژی، این توزیع اغلب برای محاسبه فرکانس های احتمالی انواع مختلف ترشحات انتقال دهنده های عصبی استفاده می شود. یا اگر یک فروشگاه ویدیویی هر جمعه شب به طور متوسط 400 مشتری داشت، احتمال اینکه 600 مشتری در هر شب جمعه وارد شوند چقدر بود؟
3- فرمول توزیع پواسون
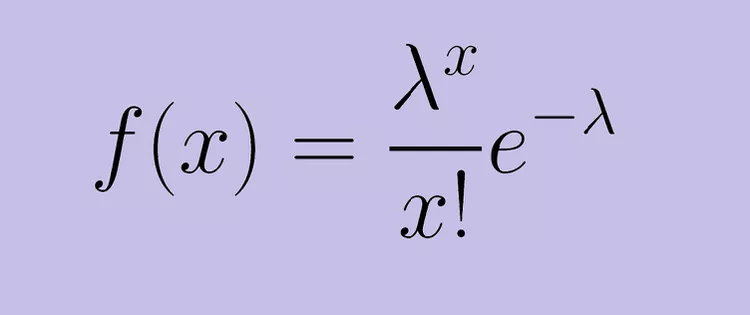
فرمول توزیع پواسون
که در آن:
- e عدد اویلر است (e = 2.71828…)
- x تعداد وقوع است
- !x فاکتوریل x است
- λ برابر است با مقدار مورد انتظار (EV) x زمانی که آن نیز برابر با واریانس آن باشد
با توجه به داده هایی که از Poisson Distribution پیروی می کنند، به صورت گرافیکی به صورت زیر ظاهر می شوند:
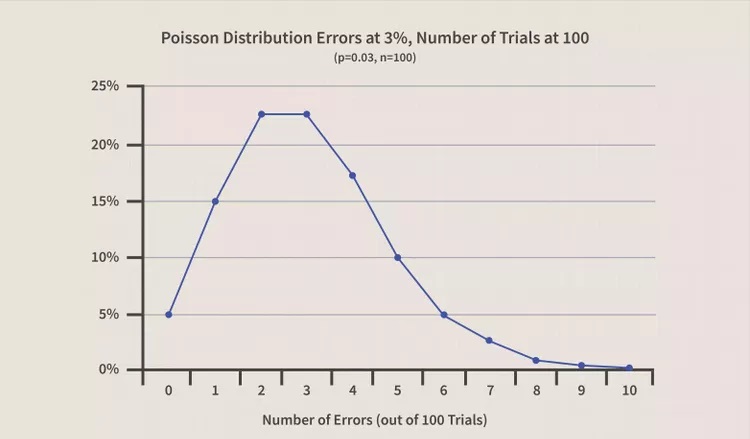
مثال Poisson Distribution
در مثال نشان داده شده در نمودار بالا، فرض کنید که برخی از فرآیندهای عملیاتی دارای نرخ خطای 3٪ هستند. اگر 100 آزمایش تصادفی را بیشتر فرض کنیم، توزیع پواسون احتمال دریافت تعداد معینی از خطاها را در یک دوره زمانی خاص، مانند یک روز منفرد، توصیف میکند.
اگر میانگین بسیار بزرگ باشد، Poisson Distribution تقریباً یک توزیع نرمال است.
4- توزیع پواسون در امور مالی
توزیع پواسون معمولاً برای مدلسازی دادههای شمارش مالی در مواردی که آمار کوچک و اغلب صفر است استفاده میشود. به عنوان یک مثال در امور مالی، می توان از آن برای مدل سازی تعداد معاملاتی که یک سرمایه گذار معمولی در یک روز معین انجام می دهد استفاده کرد که می تواند 0 (اغلب) یا 1 یا 2 و غیره باشد.
به عنوان مثالی دیگر، می توان از این مدل برای پیش بینی تعداد شوک هایی که در یک بازه زمانی معین، مثلاً در یک دهه، به بازار رخ می دهد، استفاده کرد.
5- مثال از توزیع پواسون
به طور کلی، این توزیع اغلب برای داده های شمارش مناسب است. داده های شمارش از مشاهداتی تشکیل شده است که اعداد صحیح غیر منفی هستند (یعنی اعدادی که برای شمارش استفاده می شوند، مانند 0، 1، 2، 3، 4 و غیره).
مرگ بر اثر لگد اسب
یکی از اولین کاربردهای توزیع پواسون توسط آماردان Ladislaus Bortkiewicz بود. در اواخر دهه 1800، او مرگ تصادفی توسط لگد اسب سربازان در ارتش پروس را بررسی کرد. او داده های 20 ساله 10 سپاه ارتش را تجزیه و تحلیل کرد که معادل 200 سال مشاهدات یک سپاه است.
هیستوگرام زیر داده های شبیه سازی شده را نشان می دهد که مشابه آنچه بورتکیویچ مشاهده کرده است:
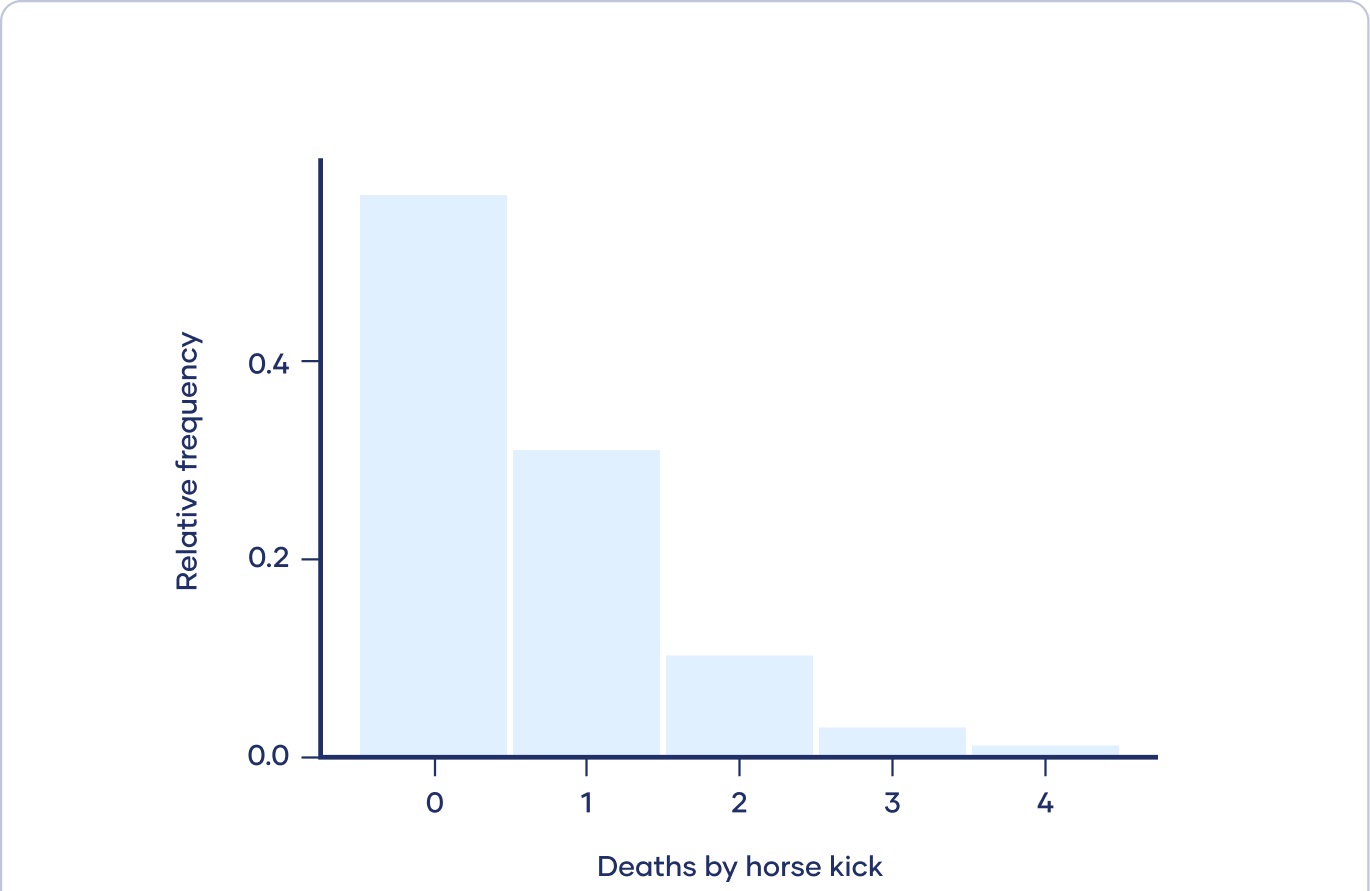
توزیع پواسون توسط آماردان Ladislaus Bortkiewicz بر مرگ تصادفی توسط لگد اسب سربازان در ارتش پروس
او دریافت که هر سال به طور میانگین 0.61 سرباز در هر سپاه در اثر لگد زدن اسب جان خود را از دست می دهند. با این حال، بیشتر سال ها، هیچ سربازی بر اثر لگد اسب نمی مرد. در سوی دیگر طیف، یک سال غم انگیز، چهار سرباز در همان سپاه بودند که بر اثر لگد اسب جان باختند.
استفاده از اصطلاحات مدرن:
- مرگ با لگد اسب یک “رویداد” است.
- فاصله زمانی یک سال است.
- میانگین تعداد رویدادها در بازه زمانی، λ، 0.61 است.
- تعداد تلفات با لگد اسب در یک سال خاص k است.
سپاه ارتشی که بورتکیویچ مشاهده کرد، نمونه ای از جمعیت تمام سپاه ارتش پروس بود. به دلیل ماهیت تصادفی نمونهگیری، نمونهها به ندرت از توزیع احتمال کامل پیروی میکنند. مرگ و میر ناشی از ضربه اسب در نمونه تقریباً از توزیع پواسون تبعیت می کند، بنابراین می توانیم به طور منطقی استنباط کنیم که جمعیت از Poisson Distribution پیروی می کند.
استفاده از فرمول توزیع پواسون
به طور متوسط 0.61 سرباز در سال در هر سپاه ارتش پروس با لگد اسب جان خود را از دست دادند. شما میخواهید این احتمال را محاسبه کنید که دقیقاً دو سرباز در سپاه هفتم ارتش در سال 1898 جان خود را از دست دادهاند، با این فرض که تعداد تلفات با لگد اسب در سال از توزیع پواسون پیروی میکند.
شروع محاسبه
سپاه خاص ارتش (سپاه ارتش هفتم) و سال (1898) مهم نیست زیرا احتمال ثابت است.
k = 2 مرگ با لگد اسب
λ = 0.61 مرگ با لگد اسب در سال
e = 2.718
!P(X = k) = e^-λ * λ^k / k
P(X = 2) = 0.101
احتمال مرگ دقیقاً دو سرباز در سپاه هفتم ارتش در سال 1898 0.101 است.
نمونه های دیگر از توزیع پواسون
از زمان Bortkiewicz، توزیع پواسون برای توصیف بسیاری از چیزهای دیگر استفاده شده است. به عنوان مثال، می تواند برای توضیح یا پیش بینی استفاده شود:
- پیامک در ساعت
- خرس گریزلی نر در هر هکتار
- خرابی ماشین در سال
- بازدیدکنندگان وب سایت در ماه
- موارد آنفولانزا در سال
6- نمودارهای تابع جرم احتمال
توزیع پواسون را می توان به صورت بصری به عنوان نمودار تابع جرم احتمال نشان داد. تابع جرم احتمال تابعی است که توزیع احتمال گسسته را توصیف می کند.
محتمل ترین تعداد رویدادها با قله توزیع – حالت نمایش داده می شود.
- وقتی λ یک عدد غیر صحیح است، حالت نزدیکترین عدد صحیح کوچکتر از λ است.
- وقتی λ یک عدد صحیح است، دو حالت وجود دارد: λ و λ-1.
وقتی λ پایین است، توزیع در سمت راست قله آن بسیار طولانی تر از سمت چپ آن است (یعنی به شدت به راست انحراف دارد right skewed).
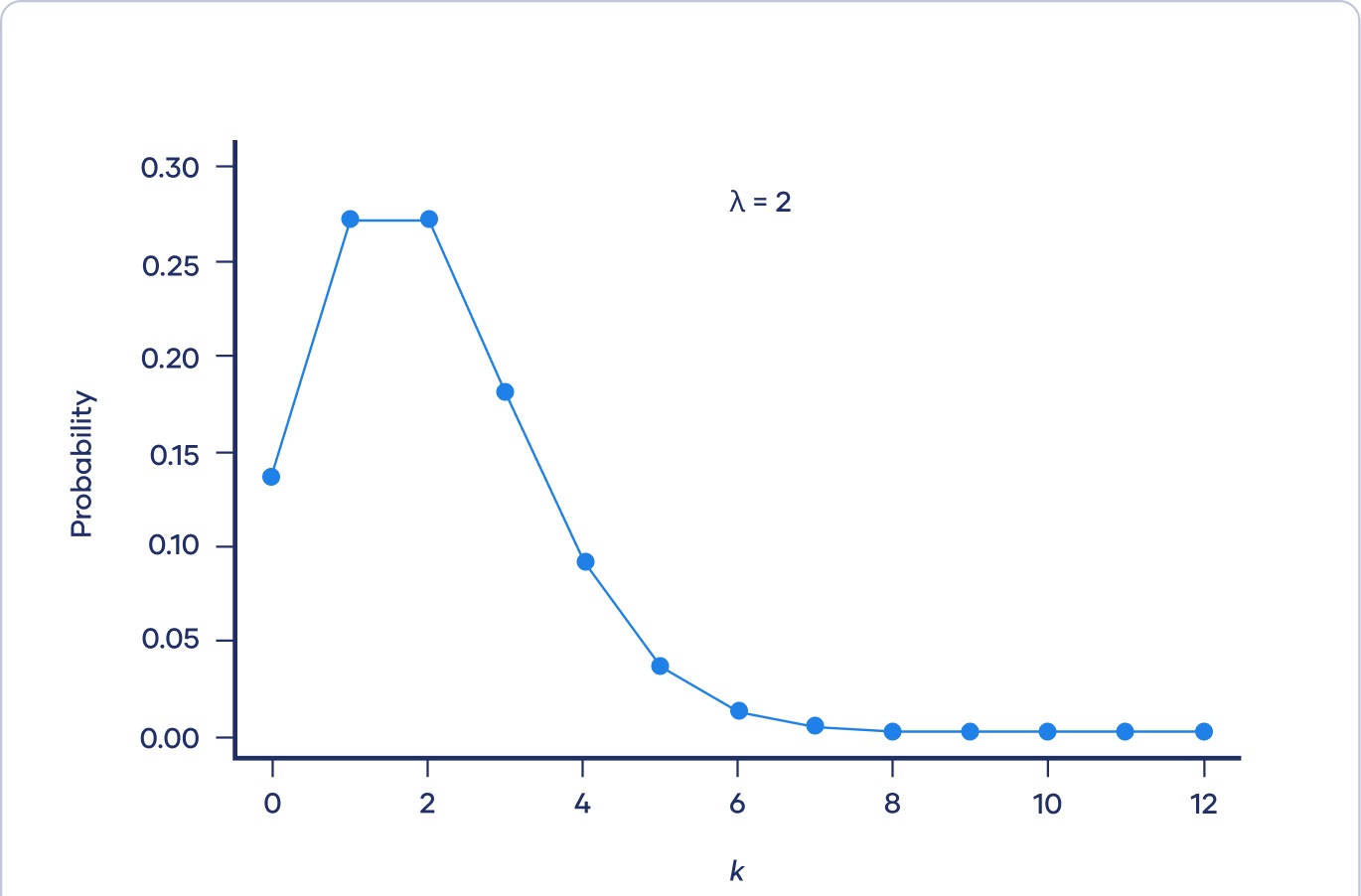
توزیع پواسون چولگی راست
با افزایش λ، توزیع بیشتر و بیشتر شبیه توزیع نرمال به نظر می رسد. در واقع، وقتی λ 10 یا بیشتر است، توزیع نرمال تقریب خوبی از توزیع پواسون است.
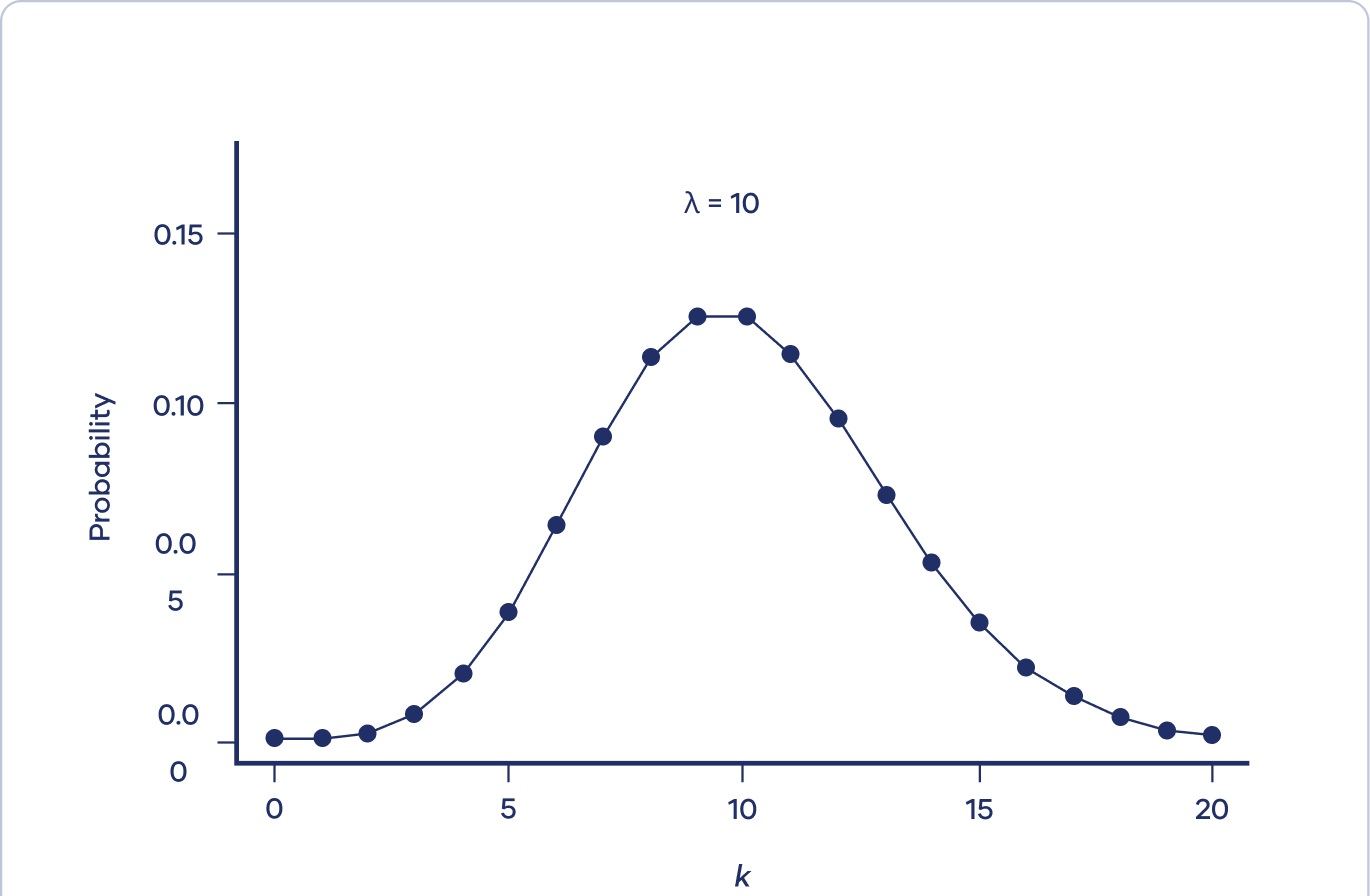
توزیع پواسون توزیع نرمال
7- میانگین و واریانس توزیع پواسون
Poisson Distribution تنها یک پارامتر دارد که λ نام دارد.
- میانگین توزیع پواسون λ است.
- واریانس توزیع پواسون نیز λ است.
در اکثر توزیعها، میانگین با μ (mu) و واریانس با σ² (سیگما مجذور) نشان داده میشود. از آنجایی که این دو پارامتر در این توزیع یکسان هستند، از نماد λ برای نمایش هر دو استفاده می کنیم.
8- سوالات پرتکرار
چه زمانی باید از توزیع پواسون استفاده کرد؟
هنگامی که متغیر مورد نظر یک متغیر شمارشی باشد، توزیع پواسون برای تحلیل آماری به بهترین وجه اعمال می شود. به عنوان مثال، چند بار X بر اساس یک یا چند متغیر توضیحی رخ می دهد. به عنوان مثال، برای تخمین تعداد محصولات معیوب از خط مونتاژ با توجه به ورودی های مختلف.
توزیع پواسون چه فرضیاتی دارد؟
برای اینکه Poisson Distribution دقیق باشد، همه رویدادها مستقل از یکدیگر هستند، نرخ رویدادها در طول زمان ثابت است و رویدادها نمی توانند به طور همزمان رخ دهند. علاوه بر این، میانگین و واریانس با یکدیگر برابر خواهند بود.
آیا توزیع پواسون گسسته است یا پیوسته؟
از آنجا که تعداد گسسته را اندازه گیری می کند، توزیع پواسون نیز یک توزیع گسسته است. این را می توان با توزیع نرمال که پیوسته است مقایسه کرد.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











