حل معادله دیفرانسیل در متلب با مثال و کد

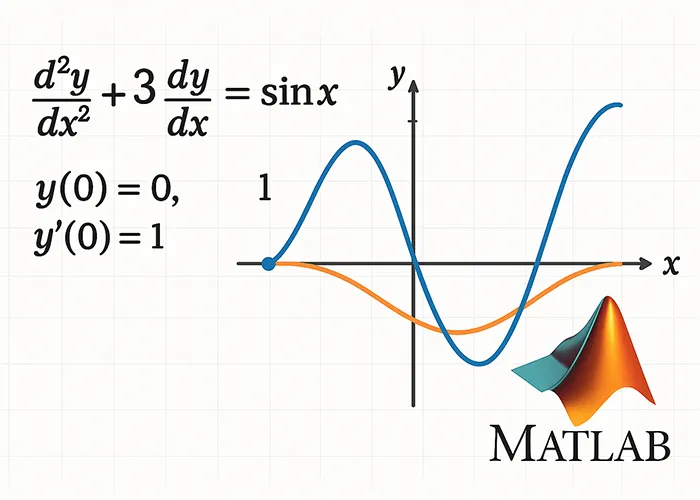
چکیده مقاله:
در علوم مهندسی و ریاضیات کاربردی، معادلات دیفرانسیل ابزاری کلیدی برای مدل سازی پدیده های فیزیکی، زیستی و اقتصادی هستند. این معادلات توصیف کننده تغییرات یک سیستم نسبت به متغیرهای مستقل مانند زمان یا مکان هستند. از آنجایی که بسیاری از این معادلات به صورت تحلیلی قابل حل نیستند، استفاده از روش های عددی برای یافتن پاسخ تقریبی آن ها ضروری است. حل معادله دیفرانسیل در متلب به عنوان یکی از قدرتمندترین روش های عددی، امکان حل معادلات دیفرانسیل معمولی (ODE)، معادلات دیفرانسیل با مشتقات جزئی (PDE) و سیستم های معادلات دیفرانسیل را فراهم می کند. این نرم افزار با استفاده از توابع داخلی متنوع، فرایند حل را ساده تر کرده و دقت بالایی در محاسبات ارائه می دهد.

متلب دارای توابع متنوعی مانند ode45، ode23، ode15s و دیگر حل کننده های عددی است که بسته به نوع معادله و ویژگی های آن، قابل استفاده هستند. این توابع بر پایه روش های عددی مانند روش رانگ کوتای مرتبه چهارم و روش های ضمنی طراحی شده اند تا دقت و پایداری بالایی در حل معادلات داشته باشند. کاربران می توانند با مشخص کردن معادله دیفرانسیل، شرایط اولیه و دامنه حل، به راحتی جواب معادله را به صورت عددی محاسبه و تحلیل کنند. علاوه بر این، متلب قابلیت نمایش نمودارهای گرافیکی از نتایج را دارد که به درک بهتر رفتار سیستم های دینامیکی کمک می کند.

مقدمه: حل معادله دیفرانسیل در متلب یکی از ابزارهای اساسی در مدل سازی می باشد و نقش مهمی در حوزه های مختلف از جمله فیزیک، اقتصاد، مهندسی و زیست شناسی ایفا می کند. این معادلات رفتار یک تابع و مشتقات آن را توصیف کرده و پویایی سیستم هایی را که در طول زمان تغییر می کنند، ثبت می نمایند. از سوی دیگر، MATLAB ابزارهای قدرتمندی برای حل عددی معادلات دیفرانسیل ارائه می دهد، چه معادلات ساده مرتبه اول باشند و چه معادلات پیچیده تر با مرتبه بالاتر .در ادامه شما را در فرآیند حل معادلات دیفرانسیل با مرتبه های مختلف راهنمایی خواهیم کرد.

• نرم افزار متلب چیست؟

حل معادله دیفرانسیل مرتبه اول در متلب

فرض کنید می خواهیم معادله زیر را حل کنیم:

y’+y=exp(-t)

به طوری که:

y(0)=1

برای حل این معادله از مراحل زیر پیروی می کنیم:

• کاربرد متلب در مهندسی شیمی

1- تعریف معادله دیفرانسیل

در اینجا،  dydt تابعی است که معادله دیفرانسیل را نمایش می دهد. باید dy/dt را به عنوان متغیر اصلی فرمول در نظر بگیریم. عبارت @(t,y) یک تابع ناشناس ایجاد می کند که متغیرهای  t و  y را نمایش می دهد.

2- مشخص کردن شرایط اولیه و بازه زمانی

3- تعریف حل کننده ODE

در MATLAB چندین حل‌کننده داخلی برای معادلات دیفرانسیل معمولی (ODE) وجود دارد، از جمله ode15s، ode23 و ode45. برای به دست آوردن حل عددی، می توان از هر یک از این توابع استفاده کرد.

متغیر t نشان دهنده نقاط زمانی است و y مقدار حل شده مربوط به هر زمان را نمایش می دهد.

• چگونه در متلب نمودار رسم کنیم؟

4- ترسیم نمودار حل معادله

این مرحله مقدار y(t) را رسم خواهد کرد .نمودار خروجی نمایش داده می شود و می توان بازه زمانی را تنظیم کرده یا نمودار را با دقت بیشتری ترسیم نمود.

• کاربردهای متلب در مهندسی پزشکی

حل معادله دیفرانسیل مرتبه دوم در متلب

فرض کنید می خواهیم معادله زیر را حل کنیم:

d²y/dt² + 5 dy/dt + 6y = 0

y(0) = 1 and y’(1) = 2

1- تبدیل معادله دیفرانسیل مرتبه دوم به دستگاهی از معادلات مرتبه اول

برای تبدیل معادله مرتبه دوم به یک سیستم از معادلات مرتبه اول، متغیرهای زیر را تعریف می کنیم:

2- تعریف دستگاه معادلات دیفرانسیل مرتبه اول

می توانیم این دستگاه را در MATLAB با استفاده از یک تابع بی‌نام (Anonymous Function) یا یک فایل جداگانه تعریف کنیم:

که در آن:

• Y(1) متناظر با y1=y می باشد.
• Y(2) متناظر با y2=dy/dt می باشد.

• کاربرد متلب در مهندسی برق

3- مشخص کردن شرایط اولیه

4- حل دستگاه با استفاده از حل کننده ODE

• t برداری از مقادیر زمان است.
• Y ماتریسی است که هر ستون آن مربوط به حل یکی از متغیرهای y1 و y2 می باشد.

• کاربردهای متلب در مهندسی عمران

5- استخراج و رسم نمودار حل معادله

این نمودار، دو تابع y1یعنی y(t) و y2یعنی dy\dt را بر حسب زمان t نمایش می دهد.

• پردازش تصویر با متلب

حل معادله دیفرانسیل مرتبه سوم در متلب

فرض کنید می خواهیم معادله زیر را حل کنیم:

y”’ – 3y” + 2y’ – y’ = cos(t)

با شرایط اولیه:

y(0) = 1, y’(0) = 0 and y”(0) = 1

1- تبدیل معادله دیفرانسیل مرتبه سوم به دستگاهی از معادلات مرتبه اول

برای تبدیل این معادله مرتبه سوم به یک سیستم از معادلات مرتبه اول، متغیرهای زیر را تعریف می کنیم:

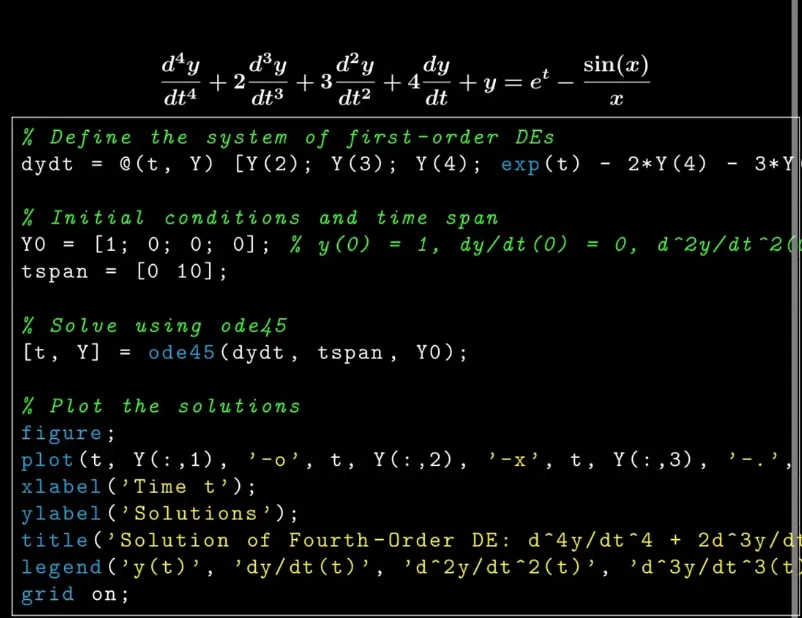
2- تعریف دستگاه معادلات دیفرانسیل در MATLAB

که در آن:

• Y(1) متناظر با y1=y می باشد.
• Y(2) متناظر با y2=dy\dt می باشد.
• Y(3) متناظر با y3=d2y/dt2y می باشد.

• روش نابجایی در متلب

3- تعیین شرایط اولیه و بازه زمانی

4- حل دستگاه با استفاده از حل‌کننده ODE

• t برداری از مقادیر زمان است.
• Y ماتریسی است که هر ستون آن مربوط به حل یکی از متغیرهای y1، y2 و y3 می باشد.

• مقایسه متلب با پایتون

5- رسم نمودار حل معادله

در اینجا، راه حل ها را به صورت جداگانه در سه زیرنمودار رسم می کنیم:

این کد، سه تابع مربوط به y1، y2 و y3 را برحسب زمان t نمایش می دهد.

• شبیه سازی بازوی ربات با متلب

حل معادله دیفرانسیل در متلب با دستور dsolve

متلب در حل معادلات دیفرانسیل بسیار قدرتمند می باشد. دستور استاندارد برای این کار dsolve (مخفف Differential Solve) است و قالب کلی آن به صورت dsolve (“معادله” ، “متغیر”) می باشد. در اینجا، معادله یک معادله دیفرانسیل است که به صورت یک رشته متنی تعریف می شود و متغیر نیز متغیر مستقل است.

به عنوان مثال، فرض کنید می خواهیم معادله y’ = 2y + x را حل کنیم. می توانیم آن را در متلب به شکل زیر وارد کنیم:

در اینجا،  Dy نمایانگر مشتق متغیر  y است. همچنین باید توجه داشت که متلب ممکن است ثابت های انتگرال گیری را با شماره های مختلفی مانند C1،  C2 و غیره نمایش دهد که این موضوع به تعداد ثابت هایی که در محاسبات قبلی در متلب ظاهر شده اند بستگی دارد. فعلاً نیازی به نگرانی درباره شماره گذاری این ثابت ها نیست.

• شبیه سازی

• نبود متغیر مستقل

معادله دیفرانسیل y’ = 3y را در نظر بگیرید. اگر این معادله را در متلب وارد کنیم:

خروجی متلب به صورت زیر خواهد بود:

می بینیم که متلب پاسخ را بر حسب  t ارائه داده است. اما چرا t؟ دلیل این امر آن است که:

1. معادله دیفرانسیل متغیر مستقلی ندارد، بنابراین متلب نمی داند که y تابع چه متغیری است.
2. t یک متغیر رایج است، زیرا در بسیاری از موارد معادلات دیفرانسیل برای توابع وابسته به زمان به کار می روند.

• مزایا و معایب زبان برنامه نویسی متلب

اگر بخواهیم متغیر دیگری مانند  x را به عنوان متغیر مستقل انتخاب کنیم، می توانیم به متلب اعلام کنیم:

خروجی:

• استفاده از مشتقات مرتبه بالاتر

می توانیم از مشتقات مرتبه بالاتر مانند  D2y و  D3y نیز استفاده کنیم. برای مثال، معادله دیفرانسیل y” = 2y را در نظر بگیرید که در آن  y تابعی از  z است. این معادله را می توان در متلب به صورت زیر حل کرد:

خروجی:

در اینجا، متلب مشتقات مرتبه دوم را نیز شناسایی کرده و ثابت های دلخواه را در پاسخ لحاظ نموده است.

• نحوه اتصال متلب به آردوینو: مراحل، مزایا و کاربردها

مسائل مقدار اولیه

ما می توانیم شرایط اولیه را نیز در متلب تعیین کنیم. در اینجا، شرط اولیه نیز به صورت یک رشته متنی تعریف می گردد.

برای مثال، حل معادله دیفرانسیل y’ = 2y با شرط اولیه y(0) = 5 در متغیر x  به صورت زیر خواهد بود:

خروجی:

• مرتبه بالاتر با چندین شرط اولیه

می توانیم معادلات دیفرانسیل مرتبه بالاتر را نیز با چندین شرط اولیه حل کنیم. به عنوان مثال، معادله y” + y’ = x با شرایط اولیه y(0) = 1 و y'(1) = 2 را به شکل زیر در متلب حل می کنیم:

خروجی:

متلب می تواند بسیاری از مسائل معادلات دیفرانسیل را بدون مشکل حل کند، همان طور که در مثال های بالا مشاهده شد. در ادامه، امکانات پیشرفته تری را بررسی خواهیم کرد.

• شبیه سازی با متلب

حل معادله دیفرانسیل در متلب با استفاده از توابع نمادین

ما می توانیم معادلات دیفرانسیل را با استفاده از توابع نمادین نیز حل کنیم. در این حالت، نحوه نگارش کاملاً متفاوت است، بنابراین باید دقت کافی داشت!

به عنوان مثال، معادله y’ = y + t را می توان با استفاده از توابع نمادین به صورت زیر حل کرد:

خروجی:

در اینجا، از تابع  syms برای تعریف  y(t) به عنوان یک تابع نمادین استفاده شده است. همچنین، در هنگام تعریف معادله از علامت  == به جای  = استفاده شده است.

• روش تنصیف در متلب

• اضافه کردن مقدار اولیه

برای حل همین معادله با مقدار اولیه y(1) = -2، کد متلب به صورت زیر خواهد بود:

خروجی:

نکته مهم این است که  y را بدون پرانتز نوشته ایم و  y(t) را در تعریف تابع استفاده نکرده ایم، زیرا در غیر این صورت متلب دچار خطا خواهد شد.

• روش ژاکوبی در متلب همراه با کد، مزایا و کاربرد

حل معادله دیفرانسیل در متلب با رسم نمودار

برای رسم نمودار در متلب، کافی است که خروجی  dsolve را در  ezplot قرار دهیم.

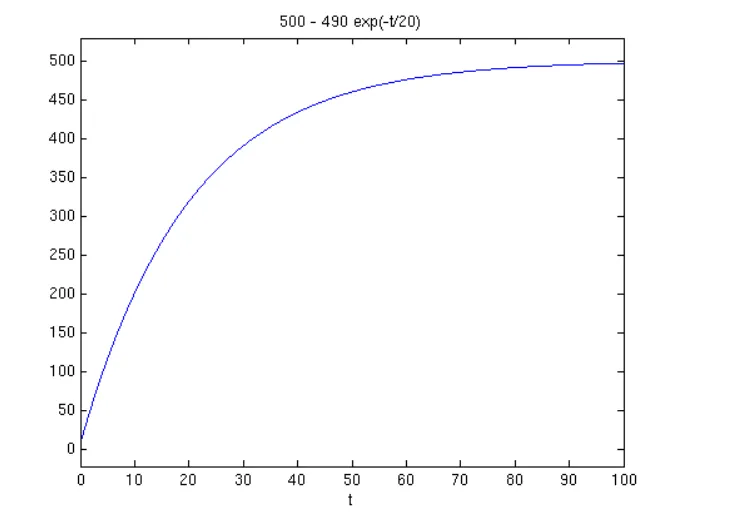
به عنوان مثال، اگر بخواهیم معادله y’ = 0.05(500 – y) را با مقدار اولیه y(0) = 10 حل کرده و نمودار آن را در بازه [0,100] رسم کنیم، از دستور زیر استفاده می کنیم:

این دستور ابتدا معادله دیفرانسیل را حل کرده و سپس آن را بر حسب  t در بازه 0 تا 100 رسم می کند.

• فرق متلب ورژن a و b چیست؟

مزایای حل معادله دیفرانسیل در متلب

متلب به دلیل توابع داخلی و روش های عددی پیشرفته، ابزاری قدرتمند برای حل معادلات دیفرانسیل محسوب می شود. این نرم افزار امکان پیاده سازی آسان الگوریتم ها، نمایش تصویری پاسخ ها و مدیریت سیستم های پیچیده را فراهم می کند. در ادامه، برخی از مزایای متلب در حل معادلات دیفرانسیل بررسی شده است:

• فرق متلب با فرترن: مزایا، کاربرد، ویژگی و نصب

1. توابع داخلی

متلب دارای توابع داخلی مانند ode45 و  ode23 می باشد که به طور ویژه برای حل معادلات دیفرانسیل معمولی (ODEs) طراحی شده اند و از نظر محاسباتی کارایی بالایی دارند.

• کد متلب گوس سایدل

2. روش های عددی

متلب روش های عددی مختلفی مانند رانگ-کوتا (Runge-Kutta) را پیاده سازی کرده است که نه تنها برای معادلات دیفرانسیل معمولی (ODEs) بلکه برای معادلات دیفرانسیل با مشتقات جزئی (PDEs) نیز قابل استفاده هستند. این قابلیت به ویژه برای حل معادلاتی که راه‌حل تحلیلی ندارند بسیار مفید است.

3. نمایش گرافیکی

متلب ابزارهای پیشرفته ای برای رسم نمودار و نمایش تصویری دارد که به کاربران کمک می کند تا رفتار سیستم را در طول زمان بهتر درک کنند.

• لگوریتم ژنتیک در متلب

4. سهولت استفاده

رابط کاربری متلب و مستندات جامع آن باعث می شود که کاربران بتوانند بدون نیاز به دانش عمیق برنامه نویسی، مدل های ریاضی پیچیده را پیاده سازی کنند.

به طور خلاصه، متلب با ارائه راه‌حل های عددی کارآمد، ابزارهای نمایش گرافیکی و سهولت استفاده، یک گزینه مناسب برای حل معادلات دیفرانسیل محسوب می شود.

• چگونه در متلب تابع تعریف کنیم؟