آزمون شاپیرو-ویلک: نحوه محاسبه و مثال عددی

چکیده مقاله:
آزمون شاپیرو-ویلک (Shapiro-Wilk Test) یکی از پرکاربردترین آزمون های آماری برای بررسی نرمال بودن داده ها می باشد. این آزمون نخستین بار توسط شاپیرو و ویلک در سال 1965 معرفی شد و به دلیل توان آماری بالای آن نسبت به بسیاری از آزمون های مشابه، در تحقیقات علمی و تحلیل های آماری گسترده ای مورد استفاده قرار گرفته است. در این آزمون فرض صفر بر نرمال بودن توزیع داده ها استوار است و در صورتی که مقدار معنی داری آزمون کمتر از سطح خطای تعیین شده (معمولا 0.05) باشد، فرض صفر رد شده و نتیجه گرفته می شود که داده ها از توزیع نرمال پیروی نمی کنند.
مزیت اصلی آزمون شاپیرو-ویلک در مقایسه با دیگر آزمون های نرمالیتی، دقت بالا و کارایی آن در نمونه های کوچک می باشد. این آزمون با محاسبه آماره ای بر اساس ترکیب خطی از داده های مرتب شده، میزان انحراف داده ها از حالت نرمال را اندازه گیری می کند. به همین دلیل بسیاری از پژوهشگران در حوزه های مختلف علوم انسانی، اجتماعی و مهندسی از این آزمون به عنوان ابزاری مطمئن برای بررسی پیش فرض نرمال بودن داده ها استفاده می کنند.
آزمون شاپیرو-ویلک یک ابزار کلیدی برای بررسی نرمال بودن داده ها است. در این مقاله، ما بررسی می کنیم که این آزمون چیست، چگونه کار می کند، مزایا و محدودیت های آن چیست، و چگونه می توان با مثال های عملی در پایتون نرمال بودن داده ها را ارزیابی کرد. همچنین تفاوت آن با سایر آزمون ها مانند t-test و روش های تصویری بررسی نرمال بودن داده ها را توضیح می دهیم تا شما بتوانید به صورت کاربردی و علمی از این آزمون در تحلیل داده های خود استفاده کنید.
آزمون شاپیرو-ویلک
آزمون شاپیرو-ویلک (Shapiro-Wilk Test) و بررسی نرمال بودن داده ها
آزمون شاپیرو-ویلک ابزاری قدرتمند برای بررسی این است که آیا یک نمونه از داده ها از توزیع نرمال تبعیت می کند یا خیر. در این آزمون، فرض صفر (Null Hypothesis) بیان می کند که داده ها به صورت نرمال توزیع شده اند. اگر مقدار p بسیار کم باشد، نشان دهنده این است که داده ها از نرمال بودن فاصله دارند و فرض صفر رد می شود.
در علم داده و آمار، اغلب لازم است که بررسی کنیم داده ها به صورت نرمال توزیع شده اند یا خیر. برای مثال، در رگرسیون خطی، یکی از شرایط استفاده صحیح از آزمون F، نرمال بودن باقی مانده ها (Residuals) است. یکی از روش های متداول برای بررسی نرمال بودن داده ها، استفاده از این آزمون است.
نرمال بودن داده ها به چه معنا است؟
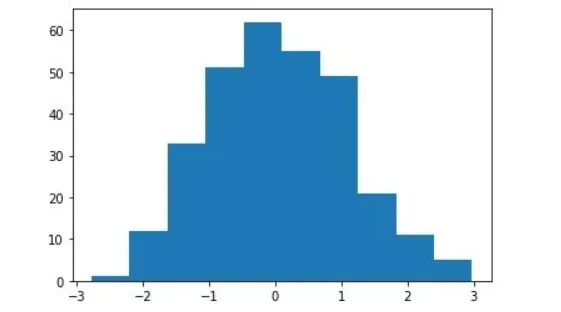
یک مثال از یک مجموعه داده با توزیع نرمال.
نرمال بودن داده ها یعنی این که یک نمونه خاص از داده ها از توزیع گاوسی (Gaussian Distribution) ایجاد شده باشد. لازم نیست این توزیع حتماً استاندارد باشد، یعنی میانگین صفر و واریانس برابر یک داشته باشد. تنها کافی است که شکل کلی داده ها شبیه توزیع نرمال باشد.
در تحلیل داده و آمار، موقعیت های مختلفی وجود دارد که داده ها باید نرمال باشند:
- برای مقایسه باقی مانده های رگرسیون خطی در مجموعه آموزشی با باقی مانده ها در مجموعه آزمایشی با استفاده از آزمون
- برای مقایسه میانگین یک متغیر در گروه های مختلف با استفاده از تحلیل واریانس یک طرفه (ANOVA) یا آزمون t دانشجویی.
- برای ارزیابی همبستگی خطی بین دو متغیر با استفاده از آزمون مناسب روی ضریب همبستگی پیرسون.
- برای بررسی اینکه آیا احتمال وقوع یک ویژگی در مقابل هدف در مدل Naive Bayes اجازه می دهد که از مدل Gaussian Naive Bayes استفاده شود.
تمام این مثال ها از موقعیت های رایج در کار روزمره یک دانشمند داده هستند. متأسفانه داده ها همیشه به صورت نرمال توزیع نمی شوند. در این شرایط، تبدیل هایی مانند روش Box-Cox یا Yeo-Johnson می توانند کمک کنند تا توزیع داده ها متقارن تر شود و نرمال بودن به شکل بهتری برقرار گردد.
یکی از روش های خوب برای بررسی نرمال بودن داده ها، استفاده از نمودار Q-Q Plot است که تصویر بصری از نرمال بودن ارائه می دهد. با این حال، گاهی نیاز داریم یک نتیجه کمی و عددی داشته باشیم و یک نمودار بصری کافی نیست. به همین دلیل از آزمون های فرضیه ای مانند آزمون شاپیرو-ویلک برای بررسی نرمال بودن نمونه ها استفاده می کنیم. این آزمون می تواند به طور دقیق نشان دهد که داده های ما چقدر به توزیع نرمال نزدیک هستند و آیا فرض نرمال بودن داده ها معتبر است یا خیر.
آزمون شاپیرو ویلک چیست؟
آزمون شاپیرو-ویلک یک آزمون فرضیه ای است که روی یک نمونه داده اعمال می شود و فرض صفر آن بیان می کند که نمونه مورد نظر از یک توزیع نرمال ایجاد شده است. اگر مقدار p کوچک باشد، می توانیم فرض صفر را رد کنیم و نتیجه بگیریم که نمونه از توزیع نرمال پیروی نمی کند.
این آزمون یکی از ابزار های آماری پرکاربرد است که می تواند پاسخ دقیقی به سوال نرمال بودن داده ها بدهد. با این حال، یک محدودیت دارد: عملکرد آن در نمونه های بزرگ چندان دقیق نیست. اندازه حداکثری مجاز برای داده ها بستگی به نحوه پیاده سازی آزمون دارد. برای مثال، در کتابخانه SciPy در زبان برنامه نویسی پایتون، نمونه هایی بزرگتر از ۵۰۰۰ هنوز قابل ارزیابی هستند، اما هشدار داده می شود که مقدار p ممکن است به دلیل محدودیت های مفروضات آزمون دقیق نباشد.
با وجود این محدودیت، این تست همچنان یک ابزار بسیار قوی و قابل اعتماد برای بررسی نرمال بودن داده ها محسوب می شود. استفاده از این آزمون به تحلیلگران داده و دانشمندان آمار این امکان را می دهد که پیش از انجام تحلیل های آماری حساس مانند رگرسیون خطی، ANOVA یا آزمون t، از نرمال بودن داده ها اطمینان حاصل کنند.
برای مثال، در پایتون می توان با استفاده از کتابخانه SciPy یک نمونه داده را بررسی کرد و مقدار p را محاسبه نمود تا مشخص شود آیا داده ها به توزیع نرمال نزدیک هستند یا خیر. این رویکرد به ویژه زمانی مفید است که بخواهیم تحلیل های آماری خود را بر اساس فرضیات دقیق انجام دهیم و از صحت نتایج اطمینان حاصل کنیم.
نحوه عملکرد آزمون شاپیرو-ویلک
Shapiro-Wilk Test با محاسبه آماره W کار می کند. این آماره بر اساس همبستگی بین داده های نمونه و مقادیر متناظر آن ها در توزیع نرمال به دست می آید. به عبارت دیگر، این آزمون بررسی می کند که ترتیب داده های نمونه چقدر با مقادیر مورد انتظار در یک توزیع نرمال مطابقت دارد.
فرمول محاسبه W به صورت زیر است:
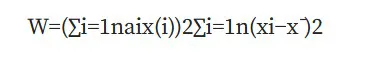
فرمول محاسبه شاپیرو-ویلک
در این فرمول:
- x(i): مقادیر نمونه مرتب شده از کوچکترین به بزرگترین هستند.
- xˉ: میانگین نمونه است.
- ai: ثابت هایی هستند که از مقادیر مورد انتظار آمار های رتبه ای (Order Statistics) در یک توزیع نرمال استخراج می شوند.
اگر داده ها به طور نرمال توزیع شده باشند، مقادیر مرتب شده نمونه باید به خوبی با مقادیر مورد انتظار یک توزیع نرمال مطابقت داشته باشند. در این حالت، آماره W نزدیک به ۱ خواهد بود. هر چه مقدار W از ۱ فاصله بیشتری داشته باشد، نشان دهنده این است که داده ها از نرمال بودن فاصله دارند و احتمال رد فرض صفر بیشتر می شود.
این ویژگی باعث می شود که آزمون ابزاری بسیار دقیق برای ارزیابی نرمال بودن داده ها باشد، به ویژه در نمونه های کوچک تا متوسط که سایر آزمون ها مانند Kolmogorov-Smirnov دقت کمتری دارند. با استفاده از این روش، تحلیلگران می توانند قبل از انجام تحلیل های آماری حساس، از صحت نرمال بودن داده ها اطمینان حاصل کنند و نتایج تحلیل خود را معتبرتر کنند.
مثال عملی آزمون شاپیرو-ویلک (Shapiro-Wilk Test) در پایتون
برای شروع، ابتدا کتابخانه های NumPy و Matplotlib را وارد می کنیم:
سپس باید تابعی را که مقدار p آزمون را محاسبه می کند، وارد کنیم. در کتابخانه scipy.stats، این تابع با نام shapiro موجود است:
حال دو مجموعه داده شبیه سازی می کنیم: یکی از توزیع نرمال و دیگری از توزیع یکنواخت (Uniform) تولید شده است.
در این مثال، مجموعه داده x نمونه ای از داده های نرمال را شبیه سازی می کند و مجموعه داده y نمونه ای از داده هایی است که توزیع آن ها یکنواخت است. هدف ما این است که با استفاده از آزمون Shapiro-Wilk Test، تفاوت بین داده های نرمال و غیر نرمال را بررسی کنیم و مقدار p را محاسبه نماییم.
در مرحله بعد، می توانیم تابع shapiro را روی هر دو مجموعه داده اجرا کنیم تا نتایج نرمال بودن آن ها را مشاهده کنیم و تحلیل کنیم که کدام مجموعه به توزیع نرمال نزدیک تر است. این کار به ما کمک می کند قبل از انجام تحلیل های آماری حساس، مانند رگرسیون یا ANOVA، از صحت نرمال بودن داده ها مطمئن شویم.
این نمودار میلهای برای “x” است:
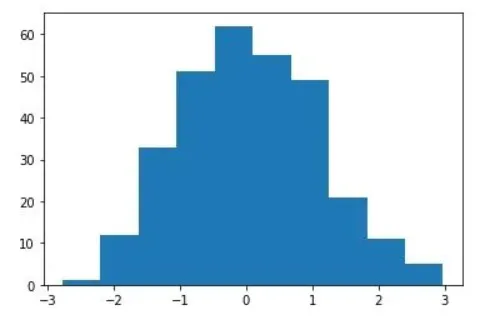
نمودار میلهای “x”.
می توان به وضوح دید که توزیع بسیار شبیه به توزیع نرمال است.
و این نمودار میلهای برای “y” است:
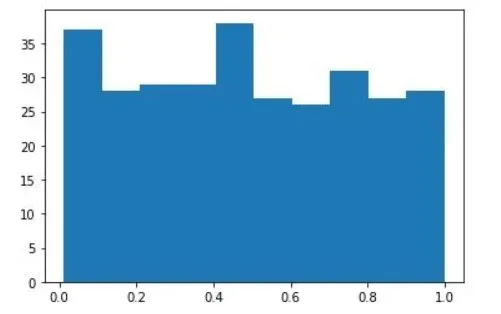
نمودار میلهای “y”.
همانطور که انتظار می رفت، توزیع فاصله زیادی با توزیع نرمال دارد.
بنابراین انتظار داریم که آزمون شاپیرو-ویلک برای نمونه “x” مقدار p نسبتاً بزرگی بدهد و برای نمونه “y” مقدار p کوچکی، زیرا این نمونه به طور نرمال توزیع نشده است.
بیایید این مقادیر p را محاسبه کنیم:
حالا می توانیم تابع shapiro را روی نمونه داده نرمال x اجرا کنیم:
همانطور که مشاهده می کنیم، مقدار p برای نمونه x به اندازه کافی کوچک نیست تا بتوانیم فرض صفر را رد کنیم. این یعنی نمونه x از نظر آماری به توزیع نرمال نزدیک است و نرمال بودن داده ها تایید می شود.
اگر همین آزمون را روی نمونه y، که از توزیع یکنواخت ایجاد شده است، اجرا کنیم:
در اینجا مقدار p کمتر از ۵ درصد است، بنابراین می توانیم فرض صفر را رد کنیم و نتیجه بگیریم که داده های نمونه y از توزیع نرمال پیروی نمی کنند.
نکته مهم: اگر بخواهیم این آزمون را روی نمونه های بزرگ تر از ۵۰۰۰ داده انجام دهیم، هشدار دریافت می کنیم:
این هشدار نشان می دهد که برای نمونه های بزرگ، مقدار p ممکن است دقیق نباشد و بهتر است از نمونه های متناسب و اندازه مناسب استفاده کنیم تا نتایج معتبر و قابل اعتماد باشند.
با استفاده از این روش، تحلیلگران داده می توانند به سرعت بررسی کنند که داده هایشان نرمال هستند یا خیر و قبل از انجام تحلیل های حساس مانند رگرسیون خطی یا تحلیل واریانس، از صحت داده ها اطمینان حاصل کنند. این مثال عملی نشان می دهد که آزمون Shapiro-Wilk Test یک ابزار ساده اما قدرتمند برای بررسی نرمال بودن داده ها در پایتون است.
مزایای استفاده از آزمون شاپیرو-ویلک

مزایای استفاده از آزمون Shapiro-Wilk
این آزمون یکی از ابزار های کلیدی برای بررسی نرمال بودن داده ها در علم داده و آمار است. این تست ساده، سریع و قابل اعتماد است و به تحلیلگران کمک می کند تا قبل از انجام تحلیل های آماری حساس، از صحت نرمال بودن داده ها اطمینان حاصل کنند. مهم ترین مزایای آن عبارتند از:
- سادگی و سهولت استفاده: اعمال این آزمون بسیار راحت است و نیاز به تنظیمات پیچیده ندارد.
- کارایی در نمونه های کوچک: یکی از مهم ترین مزایای این آزمون دقت بالای آن در نمونه های کم حجم یا داده های کوچک است.
- تکمیل فرآیند تحلیل داده: این آزمون اغلب بعد از ایجاد نمودارهای بصری مانند هیستوگرام یا Q-Q Plot استفاده می شود تا بررسی نرمال بودن داده ها کامل و دقیق انجام شود.
- پیش نیاز تحلیل های آماری: قبل از انجام تحلیل هایی مانند t-test ،ANOVA یا رگرسیون خطی، این آزمون تضمین می کند که فرض نرمال بودن داده ها برقرار است.
- ابزاری ضروری برای دانشمند داده: هر دانشمند داده باید این آزمون را در جعبه ابزار خود داشته باشد تا در تمام تحلیل های آماری که نیاز به نرمال بودن داده ها دارند، از آن بهره ببرد.
با استفاده از این مزایا، تحلیلگران می توانند تحلیل های آماری خود را با دقت و اعتماد بیشتری انجام دهند و از صحت نتایج اطمینان حاصل کنند.
سوالات متداول
آزمون شاپیرو-ویلک چه چیزی به ما می گوید؟
این آزمون نشان می دهد که یک مجموعه داده از توزیع نرمال پیروی می کند یا خیر. آزمون Shapiro-Wilk Test یک آزمون فرضیه ای است که روی نمونه داده اعمال می شود و فرض صفر آن بیان می کند که داده ها نرمال هستند. اگر مقدار p بزرگ باشد، می توان نتیجه گرفت که داده ها نرمال هستند؛ اما اگر مقدار p کوچک باشد، داده ها از توزیع نرمال فاصله دارند.
تفاوت بین t-test و Shapiro-Wilk Test چیست؟
در آمار، آزمون t برای مقایسه میانگین دو گروه داده و بررسی اختلاف معنی دار بین آن ها استفاده می شود، در حالی که آزمون شاپیرو برای بررسی این است که آیا یک مجموعه داده از توزیع نرمال پیروی می کند یا خیر. به همین دلیل، اغلب قبل از اجرای t-test ، Shapiro-Wilk Test اجرا می شود تا مطمئن شویم شرط نرمال بودن داده ها برقرار است.
چه زمانی باید از Shapiro-Wilk Test استفاده کنیم؟
این آزمون برای بررسی نرمال بودن داده ها کاربرد دارد و بیشترین دقت را در نمونه های کوچک یا داده های کم حجم دارد. بنابراین، وقتی با مجموعه داده های محدود سر و کار داریم یا می خواهیم تحلیل های آماری حساس انجام دهیم، استفاده از این آزمون بسیار توصیه می شود.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











