توزیع برنولی چیست؟ + فرمول، مثال و کاربرد در مسائل آماری

چکیده مقاله :
توزیع یک مفهوم اصلی در تجزیه و تحلیل داده، علم داده و یادگیری ماشین است. شالوده ای را برای تجزیه و تحلیل آماری یک مجموعه داده معین می گذارد و مبنایی را برای مدل های خاص یادگیری ماشین فراهم می کند. یکی از سادهترین و در عین حال مهمترین انواع توزیع، توزیع برنولی است که به نام ریاضیدان سوئیسی یاکوب برنولی نامگذاری شده است. در این پست، ما راهنمایی کامل در مورد توزیع برنولی و آزمایشات برنولی ارائه خواهیم کرد. در پایان، شما ایده روشنی از معنای واقعی توزیع برنولی خواهید داشت و اینکه کجا با بافت گستردهتر تجزیه و تحلیل دادهها مطابقت دارد. قبل از اینکه به توزیع برنولی بپردازیم، اجازه دهید ابتدا به معنای توزیع در دنیای آمار بپردازیم.
1- توزیع ها در آمار چیست؟
در آمار، توزیع تابعی است که مقادیر ممکن برای یک متغیر و تعداد دفعات وقوع آنها در یک مجموعه داده مشخص را نشان می دهد. این به شما امکان میدهد تا احتمال وقوع برخی از نتایج را محاسبه کنید و درک کنید که چه مقدار تنوع در مجموعه داده شما وجود دارد.
بیایید تصور کنیم که شما داده های شغلی 500 نفر را که در نیویورک زندگی می کنند جمع آوری کرده اید. نتایج ممکن متفاوت، همه عناوین شغلی مختلف در مجموعه داده شما هستند. از آنجایی که شغل ماهیت طبقه بندی دارد (یعنی عددی نیست)، توزیع مجموعه داده شما به شما می گوید که چند نفر (یا چند درصد) از افراد نمونه شما در هر گروه قرار دارند. مثلا 20 درصد نمونه وکیل، 10 درصد معلم، 5 درصد پرستار و … هستند.
با داده های عددی، توزیع داده ها را از کمترین به بالاترین مقدار مرتب می کند. در این حالت توزیع به صورت نمودار ارائه می شود. سپس چشم آموزش دیده می تواند به شکل نمودار نگاه کند تا در یک نگاه، نحوه توزیع داده ها را ببیند. یک توزیع به اصطلاح نرمال یک منحنی متقارن و زنگولهشکل روی یک نمودار ایجاد میکند. این نشان می دهد که بیشتر مشاهدات از خوشه داده در اطراف مرکز (یعنی مقدار میانگین) جمع می شوند و تنها تعداد کمی از مشاهدات شدیدتر از میانگین در هر دو جهت دور می شوند. توزیع نرمال به نام توزیع گاوسی یا بر اساس شکل نمودار، منحنی زنگ نیز شناخته می شود. اساساً، یک توزیع نرمال به شما می گوید که بیشتر مشاهدات (مثلاً ارتفاع) در داخل یا نزدیک به مقدار میانگین قرار می گیرند، تنها با چند نقطه پرت.
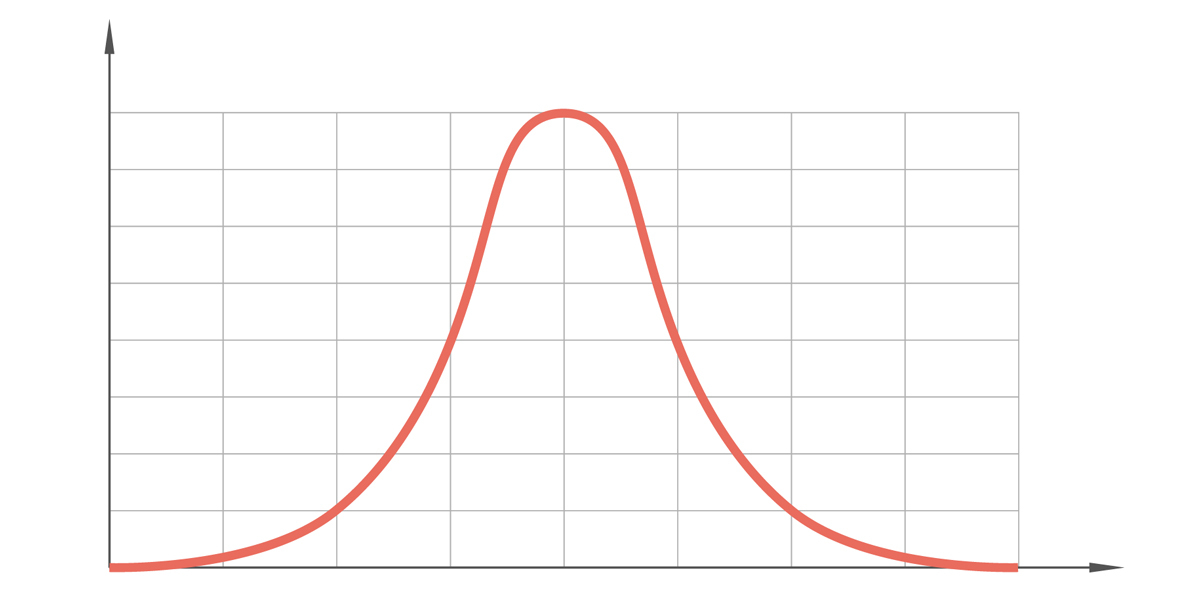
یک نمودار ساده که یک منحنی زنگوله شکل با توزیع نرمال را نشان می دهد
توزیع نرمال تنها یکی از انواع مختلف توزیع است. در این راهنما، ما بر توزیع برنولی تمرکز خواهیم کرد.
2. توزیع برنولی چیست؟
توزیع برنولی یک توزیع احتمال گسسته است، به این معنی که مربوط به متغیرهای تصادفی گسسته است. یک متغیر تصادفی گسسته، متغیری است که دارای تعداد محدود یا قابل شمارش مقادیر ممکن است – تعداد سرهایی که هنگام پرتاب سه سکه به طور همزمان به دست می آورید یا تعداد دانش آموزان یک کلاس.
بنابراین: یک توزیع احتمال گسسته، احتمال رخ دادن هر مقدار ممکن از یک متغیر تصادفی گسسته را توصیف میکند – برای مثال، احتمال به دست آوردن شش در هنگام پرتاپ یک طاس. هنگام برخورد با متغیرهای گسسته، احتمال هر مقدار بین 0 و 1 قرار می گیرد و مجموع همه احتمالات برابر با 1 است. بنابراین، در مثال طاس، با فرض استفاده از یک قالب استاندارد، احتمال آمدن 6 در پرتاب یک طاس 0.167 یا 16.7٪ است. این بر اساس تقسیم 1 (مجموع همه احتمالات) بر 6 (تعداد نتایج ممکن) است.
به طور خلاصه این توزیع احتمال گسسته است. پس توزیع برنولی چطور؟
3- توزیع برنولی و آزمایشات برنولی
توزیع برنولی برای رویدادهایی اعمال می شود که یک آزمایش و دو نتیجه ممکن دارند. اینها به عنوان آزمایشات برنولی شناخته می شوند. به هر نوع آزمایشی فکر کنید که یک سوال بله یا خیر بپرسد – برای مثال، آیا وقتی این سکه را برگردانم روی سر فرود می آید؟ آیا با این طاس یک شش رو می کنم؟ آیا از این دسته از کارت ها یک آس انتخاب خواهم کرد؟ آیا رای دهنده X در یک همه پرسی سیاسی به «آری» رأی خواهد داد؟ آیا دانش آموز Y در آزمون ریاضی خود موفق خواهد شد؟
شما ایده را دریافت می کنید. در آزمایشهای برنولی، دو نتیجه ممکن را میتوان در قالب «موفقیت» یا «شکست» در نظر گرفت – اما این برچسبها را نباید به معنای واقعی کلمه در نظر گرفت. در این زمینه، “موفقیت” به سادگی به معنای دریافت یک نتیجه “بله” است (به عنوان مثال، آوردن یک شش، انتخاب یک آس، و غیره).
توزیع برنولی اساساً محاسبهای است که به شما امکان میدهد مدلی برای مجموعه نتایج احتمالی یک آزمایش برنولی ایجاد کنید. بنابراین، هر زمان که رویدادی دارید که فقط دو نتیجه ممکن دارد، توزیع برنولی شما را قادر میسازد تا احتمال هر نتیجه را محاسبه کنید.
4- تفاوت بین توزیع برنولی و توزیع دو جمله ای چیست؟
در حالی که با توزیع برنولی دست و پنجه نرم می کنید، احتمالاً با اصطلاح دیگری برخورد کرده اید: توزیع دو جمله ای. بنابراین تفاوت بین این دو چیست و چگونه با یکدیگر ارتباط دارند؟
به عبارت بسیار ساده، توزیع برنولی نوعی توزیع دو جمله ای است. ما می دانیم که توزیع برنولی در مورد رویدادهایی اعمال می شود که یک آزمایش (1 = n) و دو نتیجه ممکن دارند – برای مثال، یک چرخش سکه (این آزمایش است) و یک نتیجه از سرها یا دم ها. وقتی بیش از یک آزمایش داریم – مثلاً یک سکه را پنج بار برمیگردانیم – توزیع دوجملهای توزیع احتمال گسسته تعداد “موفقیتها” را در آن دنباله از ورقها (یا آزمایشهای) سکه مستقل میدهد.
بنابراین، برای ادامه مثال پرتاب سکه: توزیع برنولی به شما احتمال “موفقیت” (مثلاً فرود آمدن روی سرها) را هنگام پرتاب سکه فقط یک بار (این آزمایش برنولی شما است) می دهد. اگر سکه را پنج بار بچرخانید، توزیع دوجملهای احتمال موفقیت (فرود روی سر) را در تمام پنج چرخش سکه محاسبه میکند.
این یک نمای کلی بسیار ساده است – در اینجا توضیح دقیق تری از توزیع دوجمله ای خواهید یافت. در حال حاضر، اجازه دهید با چند مثال به توزیع برنولی بازگردیم.
5- مثال از توزیع برنولی
مثال توزیع برنولی: پرتاب سکه
مثال پرتاب سکه شاید ساده ترین راه برای توضیح توزیع برنولی باشد. بیایید بگوییم که نتیجه “سرها” یک “موفقیت” است، در حالی که نتیجه “دم” یک “شکست” است. در این مورد:
- احتمال یک نتیجه موفقیت آمیز (فرود روی سر) به صورت p نوشته می شود
- احتمال شکست (فرود روی دم)، که به صورت q نوشته شده است، P **–** 1 محاسبه می شود.
با یک سکه استاندارد، ما می دانیم که 50/50 شانس فرود بر روی سر یا دم وجود دارد. بنابراین، در این مورد:
p = 0.5
q = 1– **0.5
بنابراین، در مثال پرتاب سکه، هم p و هم q = 0.5 است. در یک نمودار، احتمال شکست را به صورت “0” و احتمال موفقیت را به صورت “1” نشان می دهید، هر دو در محور y.

احتمال وقوع سر در پرتاب یک طاس
مثال دیگر از توزیع برنولی
مثال پرتاب سکه بسیار ساده است، اما در واقع سناریوهای زیادی در زندگی وجود دارد که نتیجه بله و خیر دارند. مثلا:
- آیا در یک آزمون موفق می شوید یا مردود می شوید؟
- آیا تیم ورزشی مورد علاقه شما در مسابقه بعدی خود پیروز می شود یا بازنده؟
- آیا برای آن شغلی که درخواست داده اید پذیرفته می شوید یا رد می شوید؟
- آیا در دور ابتدایی بازی رومیزی مورد علاقه خود یک شش می زنی؟
- آیا در لاتاری برنده می شوید یا بازنده؟
در این مقاله،توضیح میدهیم که چگونه آزمایشهای برنولی و توزیع برنولی میتوانند به شما کمک کنند تا بفهمید قبل از شروع به کار، چند درخواست شغلی باید ارسال کنید. توزیع برنولی همچنین در پزشکی و آزمایشات بالینی برای مدل سازی میزان موفقیت یک داروی خاص یا نتیجه یک کارآزمایی بالینی استفاده می شود. به عنوان مثال، هنگام توسعه یک داروی جدید، دانشمندان داروسازی می توانند از توزیع برنولی برای محاسبه احتمال درمان یا عدم درمان یک فرد با کمک داروی جدید استفاده کنند. توزیع های برنولی نیز در رگرسیون لجستیک برای مدل سازی وقوع بیماری استفاده می شود.
6- کاربرد توزیع برنولی
استفاده از روش برنولی آسان است، به ویژه زمانی که یک آزمایش تنها دو نتیجه را ارائه می دهد – موفقیت یا شکست. این روش در علوم داده، کاوی، یادگیری ماشینی، تجزیه و تحلیل، پزشکی، مالی، آمار و ورزش کاربرد دارد.
به عنوان مثال، با استفاده از این ابزار می توان احتمال عوارض جانبی ناشی از یک داروی جدید را اندازه گیری کرد. می تواند احتمال موفقیت یا شکست یک آزمایش پزشکی را تعیین کند. برای سنجش احتمال اسپم بودن ایمیل استفاده می شود. در بازاریابی، این قضیه احتمال خرید یا عدم خرید یک محصول خاص توسط مشتری را پیش بینی می کند.
این روش به طور موثر احتمال قبولی یا عدم موفقیت دانش آموز در آزمون را پیش بینی می کند. یک محقق می تواند شانس انتخاب یا رد یک استخدامی را تعیین کند. همچنین می تواند احتمال برد یا باخت یک شرط را پیش بینی کند.
7. شرایط توزیع برنولی چیست؟
برای کمک به درک زمان و نحوه اعمال توزیع برنولی، در نظر گرفتن شرایط آزمایشات برنولی مفید است. یک رویداد یا آزمایش تنها زمانی میتواند به عنوان آزمایش برنولی در نظر گرفته شود (و در نتیجه برای توزیع برنولی مرتبط باشد) که این معیارها را داشته باشد:
- تنها دو نتیجه ممکن از آزمایش وجود دارد. اندیشیدن به این موضوع بر حسب «موفقیت» یا «شکست» است. به عبارت دیگر، آیا آزمایش شما سؤال «بله» یا «نه» را مطرح میکند؟ به مثال های قبلی ما فکر کنید، مانند “آیا دانش آموز X امتحان ریاضی خود را قبول می شود؟” یا “آیا بیمار Y با مصرف این دارو درمان می شود؟”
- هر یک از این دو پیامد، احتمال وقوع ثابتی دارند. به عبارت دیگر، مهم نیست که چند بار یک سکه را بچرخانید، احتمال فرود روی سرها ثابت است. از نظر ریاضی، احتمال موفقیت همیشه p است و احتمال شکست همیشه p – 1 است.
- آزمایشات کاملاً مستقل از یکدیگر هستند. نتیجه یک آزمایش (مثلاً اولین ورق سکه) مطلقاً هیچ تأثیری بر نتیجه هر ورق سکه بعدی ندارد.
اگر سناریویی هر سه این معیار را داشته باشد، می توان آن را یک کارآزمایی برنولی در نظر گرفت. اکنون با توزیع برنولی آشنا شدهایم، بیایید در نظر بگیریم که کجا در زمینههای گستردهتر تجزیه و تحلیل داده، علم داده، و یادگیری ماشین کاربرد دارد.
8. توزیع برنولی در تجزیه و تحلیل داده، علم داده و یادگیری ماشین
توزیع احتمال، مانند توزیع برنولی، نه تنها برای ریاضیدانان و آماردانان مفید است بلکه نقش مهمی در تجزیه و تحلیل داده، علم داده و یادگیری ماشین دارد. تحلیلگران داده و دانشمندان داده با حجم زیادی از داده ها کار می کنند، و نگاه کردن به توزیع یک مجموعه داده معین، بخش مهمی از تجزیه و تحلیل داده های اکتشافی است – یعنی قبل از تحقیق بیشتر، درک اولیه از داده های خود را به دست آورید.
در یادگیری ماشین، بسیاری از مدلها بر اساس مفروضات توزیع کار میکنند و توزیع برنولی (و سایر توزیعهای احتمال گسسته) عمدتاً در مدلسازی مسائل طبقهبندی باینری و چند کلاسه استفاده میشوند. برخی از نمونههای مدلهای طبقهبندی باینری عبارتند از فیلترهای هرزنامه که تشخیص میدهند ایمیل باید بهعنوان «هرزنامه» یا «نه هرزنامه» طبقهبندی شود، مدلهایی که میتوانند پیشبینی کنند که آیا مشتری اقدام خاصی انجام خواهد داد یا نه، یا طبقهبندی یک محصول به عنوان مثال، یک کتاب یا یک فیلم نمونه ای از مدل طبقه بندی چند طبقه می تواند مدلی باشد که مشخص می کند کدام دسته از محصولات بیشتر مربوط به یک مشتری خاص است.
به عنوان یکی از توزیع های ساده تر، توزیع برنولی اغلب به عنوان نقطه شروع برای توزیع های پیچیده تر عمل می کند. به عنوان مثال، فرآیند برنولی پایه و اساس توزیع دوجملهای، توزیع هندسی و توزیع دوجملهای منفی را ایجاد میکند که همگی نقش مهمی در یادگیری عمیق دارند.
بنابراین، اگر میخواهید عمیقتر در تجزیه و تحلیل داده، علم داده، یا یادگیری ماشین تحقیق کنید، توزیعهای احتمال، مانند توزیع برنولی، نقطه خوبی برای شروع هستند.
7- سوالات متداول
1. آیا توزیع برنولی گسسته است یا پیوسته؟
توزیع برنولی یک احتمال گسسته تک متغیره است که در آن آزمایش تصادفی تنها دو نتیجه ممکن را ارائه می دهد – موفقیت یا شکست.
2. چه زمانی از توزیع برنولی استفاده کنیم؟
از آن برای آزمایشهای تصادفی برنولی استفاده میشود، جایی که یک رویداد فقط میتواند دو نتیجه ممکن داشته باشد – موفقیت یا شکست. معمولاً در آمار، یادگیری ماشین، علم داده، تجزیه و تحلیل، امور مالی، علوم پزشکی و غیره استفاده می شود.
3. تفاوت بین توزیع برنولی و توزیع دو جمله ای چیست؟
توزیع برنولی احتمال یک آزمایش تصادفی یا آزمایش برنولی را تعیین می کند. توزیع دو جمله ای احتمال تعداد N آزمایش برنولی را تعیین می کند.
جمع بندی:
در این پست، توزیع برنولی را معرفی کردیم. مفهومی که ارزش آن را دارد که اگر به دنبال شغلی در هر نوع زمینه مرتبط با داده هستید، با آن آشنا شوید. به طور کلی:
- توزیع برنولی یک توزیع احتمال گسسته است
- احتمال دستیابی به “موفقیت” یا “شکست” از آزمایش برنولی را توصیف می کند.
- آزمایش برنولی رویدادی است که تنها دو نتیجه ممکن (موفقیت یا شکست) دارد. به عنوان مثال، آیا یک سکه بر سر (موفقیت) یا دم (شکست) فرود می آید؟
پس توزیع برنولی نوعی توزیع دوجمله ای است.
مدیر2025-07-06T14:43:33+03:30جولای 6, 2025|0 Comments
چکیده مقاله: کاربرد برنامه نویسی در مهندسی عمران نقش بسیار مهمی در افزایش دقت، سرعت و بهره وری در انجام پروژه های عمرانی ایفا می کند. با توجه به پیچیدگی تحلیل های سازه ای، [...]
مدیر2025-07-05T13:53:05+03:30جولای 5, 2025|0 Comments
چکیده مقاله: تفاوت برنامه نویسی شی گرا و ساخت یافته یکی از موضوعات مهم در درک مفاهیم پایه ای علوم کامپیوتر و طراحی نرم افزار می باشد. برنامه نویسی ساخت یافته رویکردی است که [...]
مدیر2025-07-03T23:23:36+03:30جولای 3, 2025|0 Comments
چکیده مقاله: بهترین زبان برنامه نویسی برای بازی سازی یکی از موضوعات پرطرفدار در میان علاقه مندان به دنیای گیم و توسعه نرم افزار است. انتخاب زبان مناسب نقش مهمی در موفقیت پروژه های [...]
مدیر2025-07-03T22:06:27+03:30جولای 3, 2025|0 Comments
چکیده مقاله: تفاوت برنامه نویسی سمت سرور و کلاینت یکی از مباحث اساسی در توسعه نرم افزارهای تحت وب و اپلیکیشن ها می باشد. در برنامه نویسی سمت کلاینت، کدها در مرورگر کاربر اجرا [...]
مدیر2025-07-02T13:22:19+03:30جولای 2, 2025|0 Comments
چکیده مقاله: بهترین زبان برنامه نویسی برای هوش مصنوعی موضوعی است که ذهن بسیاری از علاقه مندان به فناوری، برنامه نویسان و پژوهشگران حوزه هوش مصنوعی را به خود مشغول کرده است. با توجه [...]
مدیر2025-07-01T15:41:45+03:30جولای 1, 2025|0 Comments
چکیده مقاله: بهترین زبان برنامه نویسی برای مهاجرت یکی از مهم ترین دغدغه های افرادی است که قصد دارند از طریق مهارت های فنی وارد بازار کار بین المللی شوند. با رشد روز افزون [...]