روش تنصیف در متلب: کاربرد، ویژگی و کد نمونه
چکیده مقاله:
روش تنصیف در متلب (Bisection Method) یکی از ساده ترین، قابل اطمینان ترین و آسان ترین روش ها برای پیاده سازی با تضمین همگرایی جهت یافتن ریشه حقیقی معادلات غیرخطی می باشد. این روش همچنین با نام های جستجوی دودویی، نیمه بازه، دوبخشی یا روش بولتسانو شناخته می شود. این روش از نوع بازه بسته بوده و نیاز به دو مقدار اولیه دارد. همگرایی آن خطی است و به طور کلی دقت خوبی ارائه می دهد. در مقایسه با سایر روش های یافتن ریشه، به دلیل نرخ همگرایی کند و پایدار، نسبتاً آهسته در نظر گرفته می شود. در ادامه قصد داریم کد با روش تنصیف در متلب را بنویسیم و سپس به مزایا، معایب، ویژگی ها و کاربردهای این روش یافتن ریشه حقیقی بپردازیم.
روش تنصیف در متلب چیست؟
روش تنصیف در متلب یکی از روش های عددی پرکاربرد برای یافتن ریشه های معادلات غیرخطی می باشد. این روش که به نام های نصف کردن بازه یا روش دو بخشی نیز شناخته می شود، بر پایه کاهش تدریجی طول بازه ای است که در آن ریشه تابع قرار دارد. روش تنصیف از یک بازه ابتدایی که شامل ریشه می باشد شروع کرده و با تقسیم مداوم این بازه به دو نیمه، محدوده ای که ریشه در آن قرار دارد را کوچک تر می کند تا به مقدار تقریبی مطلوب برسد.
این روش بر اساس تغییر علامت تابع در یک بازه کار می کند. اگر تابع در دو انتهای یک بازه دارای علامت های متفاوتی باشد، بر اساس قضیه مقدار میانی، حداقل یک ریشه در این بازه وجود دارد. در هر گام از الگوریتم، مقدار میانی بازه انتخاب می شود و مقدار تابع در آن نقطه محاسبه می گردد. سپس بسته به علامت این مقدار، یکی از دو نیمه بازه انتخاب شده و الگوریتم ادامه پیدا می کند تا خطای محاسباتی به مقدار مورد نظر برسد.
روش تنصیف به دلیل سادگی و تضمین همگرایی به عنوان یکی از روش های پایه ای حل معادلات غیرخطی شناخته می شود. با این حال، سرعت همگرایی آن نسبت به روش هایی مانند نیوتن رافسون کمتر می باشد. در متلب، این روش را می توان با استفاده از یک حلقه while یا for و شرط های مربوط به تغییر علامت تابع پیاده سازی کرد. همچنین، توابع آماده ای برای اجرای این روش در جعبه ابزارهای عددی متلب وجود دارند که می توانند به سادگی مورد استفاده قرار گیرند.
معادل انگلیسی: Bisection Method
نام های دیگر: Half Interval Method, Dichotomy Method
ویژگی های روش تنصیف در متلب
در این بخش، تمامی ویژگی های این روش برای یافتن ریشه حقیقی معادلات غیرخطی را فهرست می کنیم. روش دو بخشی دارای ویژگی های زیر می باشد:
نوع روش
روش تنصیف یک روش محصورسازی است. این بدان معناست که ریشه در یک بازه مشخص که مقدار تابع در دو انتهای آن دارای علامت مخالف است، محصور می شود. در هر تکرار، این بازه کوچک تر شده و مقدار ریشه با دقت بیشتری مشخص می گردد.
همگرایی
روش تنصیف دارای همگرایی تضمین شده است. در صورتی که بازه اولیه به درستی انتخاب شود و تابع در آن پیوسته باشد، این روش همیشه به یک مقدار همگرا خواهد شد. این ویژگی باعث می شود که روش تنصیف یکی از مطمئن ترین روش ها برای یافتن ریشه های معادلات غیرخطی باشد.
نرخ همگرایی
روش تنصیف دارای نرخ همگرایی خطی است که اگرچه کند است، اما پایدار می باشد. این بدان معناست که سرعت همگرایی این روش نسبت به روش هایی مانند نیوتن-رافسون کمتر است، اما در عوض از نوسانات ناگهانی در مقدار ریشه جلوگیری می کند و روندی مطمئن دارد.
دقت
روش تنصیف دارای دقت مناسبی می باشد. با افزایش تعداد تکرارها، بازه محدودکننده ریشه کوچک تر شده و مقدار ریشه با دقت بیشتری محاسبه می شود. میزان دقت این روش به تعداد دفعات اجرای الگوریتم بستگی دارد و می توان با انجام تکرارهای بیشتر، خطای محاسباتی را کاهش داد.
تعداد مقادیر اولیه مورد نیاز
در روش تنصیف، تنها دو مقدار اولیه مورد نیاز است که به عنوان دو حدس اولیه برای بازه انتخاب می شوند. این دو مقدار باید به گونه ای باشند که مقدار تابع در آن ها دارای علامت مخالف باشد. این ویژگی باعث می شود که انتخاب مقادیر اولیه در این روش ساده باشد و نیازی به مشتقات یا تخمین های پیچیده نباشد.
پیاده سازی در برنامه نویسی
روش تنصیف از نظر پیاده سازی بسیار ساده و آسان است. این روش تنها شامل چند عملیات ابتدایی مانند محاسبه مقدار میانی، ارزیابی تابع و تقسیم بازه به نیمه های کوچکتر می باشد. به همین دلیل، می توان آن را به راحتی در زبان های برنامه نویسی مختلف از جمله متلب پیاده سازی کرد.
رویکرد
روش تنصیف از رویکرد یافتن نقطه میانی و استفاده از روش نیمه بازه برای تعیین ریشه بهره می برد. در هر مرحله، نقطه میانی بازه محاسبه شده و مقدار تابع در این نقطه بررسی می شود. سپس بازه جدید به نحوی انتخاب می گردد که مقدار تابع در دو انتهای آن دارای علامت مخالف باشد. این فرآیند تا زمانی ادامه پیدا می کند که بازه به حد کافی کوچک شود و مقدار ریشه به دقت مطلوب برسد.
استنتاج ریاضی روش تنصیف در متلب
روش دو بخشی یک متد محصورسازی می باشد و با دو مقدار اولیه، فرضاً x0 و x1، آغاز می شود به گونه ای که این دو مقدار ریشه را محصور می کنند، یعنی:
f(x0)f(x1) < 0
این روش بر این اصل استوار است که اگر f(x) یک تابع حقیقی و پیوسته باشد و دو مقدار اولیه x0 و x1 به گونه ای انتخاب شوند که: f(x0)f(x1) < 0، در این صورت حداقل یک ریشه بین x0 و x1 وجود دارد.
در روش تنصیف در متلب، ریشه از طریق تقسیم متوالی بازه به دست می آید، به این صورت که اگر x0 و x1 دو مقدار اولیه باشند، مقدار تقریبی جدید ریشه را به صورت زیر محاسبه می کنیم:
x2 = (x0 + x1)/2
اکنون سه حالت مختلف به صورت زیر داریم:
- اگر f(x2)=0 باشد، در این صورت ریشه برابر با x2 است.
- اگر f(x0)f(x2)<0 باشد، ریشه بین x0و x2 قرار دارد.
- اگر f(x0)f(x2)>0 باشد، ریشه بین x1 و x2 قرار دارد.
سپس این فرآیند تکرار می شود تا زمانی که ریشه با دقت مورد نظر به دست آید.
روش تنصیف بر اساس قضیه مقدار میانی بنا شده است. بر اساس این قضیه:
“اگر تابع f(x) در بازه [a,b] یک تابع پیوسته باشد و مقدار c عددی بین f(a) و f(b) باشد، آنگاه حداقل یک مقدار x در این بازه وجود دارد به طوری که f(x)=c باشد.”
قضیه مقدار میانی را می توان به صورت نموداری به شکل زیر نمایش داد:
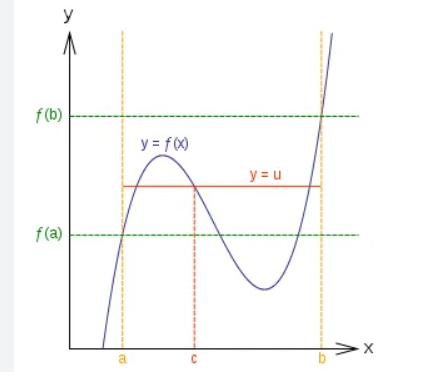
نمودار قضیه مقدار میانی
مثال کد متلب با روش تنصیف
این برنامه روش تنصیف در متلب را برای یافتن ریشه حقیقی یک معادله غیرخطی پیاده سازی می کند. در این برنامه MATLAB، متغیر y نشان دهنده تابع غیرخطی است، a و b دو مقدار اولیه (حدس اولیه) هستند و e مقدار خطای قابل تحمل می باشد.
مزایای روش تنصیف در متلب
در تحلیل عددی (روش های عددی)، روش تنصیف یکی از ساده ترین روش ها با تضمین همگرایی برای یافتن ریشه حقیقی معادلات غیرخطی می باشد. این روش که با نام دیگری نیز شناخته می شود، دارای مزایا و ویژگی های زیر است:
تضمین همگرایی
روش تنصیف در متلب یک روش محصورسازی است و همیشه همگرا می باشد. این ویژگی به این معنی است که اگر بازه اولیه به درستی انتخاب شود و ریشه درون این بازه قرار داشته باشد، روش تضمین می کند که با انجام تکرارهای متوالی به ریشه نزدیک خواهیم شد. این خاصیت باعث شده است که روش تنصیف یکی از مطمئن ترین روش ها برای یافتن ریشه معادلات غیرخطی باشد.
قابل کنترل بودن خطا
در روش تنصیف، خطا به راحتی قابل کنترل می باشد. با افزایش تعداد تکرارها، مقدار ریشه با دقت بیشتری محاسبه می شود و می توان میزان دقت را با توجه به نیاز تعیین کرد. در هر مرحله از این روش، مقدار خطا کاهش یافته و به مرور به مقدار دقیق ریشه نزدیک تر می شود، بنابراین می توان با مشخص کردن تعداد تکرارها، کنترل مناسبی روی میزان خطا داشت.
عدم نیاز به محاسبات پیچیده
یکی از مهم ترین مزایای روش تنصیف این است که نیازی به محاسبات پیچیده ندارد. در هر مرحله از این روش، تنها میانگین دو مقدار انتهای بازه محاسبه شده و مقدار تابع در این نقطه بررسی می شود. به دلیل سادگی این عملیات، اجرای روش به راحتی امکان پذیر است و حتی افرادی که آشنایی زیادی با محاسبات عددی ندارند می توانند آن را در متلب پیاده سازی کنند.
تضمین حد خطا
روش تنصیف دارای تضمین حد خطا می باشد که در هر مرحله به نصف مقدار قبلی کاهش می یابد. این ویژگی به این معنا است که می توان با اطمینان مشخص کرد که پس از تعداد معینی از تکرارها، مقدار خطا از حد مشخصی کمتر خواهد شد. این خاصیت روش را بسیار دقیق و قابل پیش بینی می کند و به کاربران اجازه می دهد تا مقدار خطای نهایی را کنترل کنند.
سادگی در پیاده سازی
سادگی در پیاده سازی یکی دیگر از مزایای مهم روش تنصیف است. این روش دارای مراحل مشخص و ساده ای می باشد که باعث می شود بتوان آن را به راحتی در زبان های برنامه نویسی مختلف از جمله متلب پیاده سازی کرد. بسیاری از الگوریتم های عددی دارای پیچیدگی های فراوانی هستند، اما روش تنصیف با داشتن یک ساختار ساده، یکی از آسان ترین روش ها برای یافتن ریشه معادلات غیرخطی محسوب می شود.
سرعت در یافتن چندین ریشه
روش تنصیف در یافتن چندین ریشه نیز سرعت بالایی دارد. اگر معادله دارای چندین ریشه در بازه های مختلف باشد، می توان با استفاده از این روش هر ریشه را به صورت مجزا و در زمان کوتاهی محاسبه کرد. با تقسیم بندی مناسب بازه ها و اعمال روش تنصیف در هر بازه، امکان یافتن تمامی ریشه های معادله با دقت بالا فراهم می شود.
معایب روش تنصیف در متلب
در تحلیل عددی (روش های عددی)، روش دو بخشی یکی از ساده ترین روش ها با تضمین همگرایی برای یافتن ریشه حقیقی معادلات غیرخطی می باشد. با این حال، علی رغم تضمین همگرایی، این روش دارای نرخ همگرایی پایینی است.
در این بخش، به بررسی معایب مختلف این متد می پردازیم:
نرخ همگرایی پایین
با وجود تضمین همگرایی، روش تنصیف معمولاً سرعت همگرایی کمی دارد. در این روش، هر بار بازه به نصف کاهش می یابد که منجر به روندی کند در نزدیک شدن به ریشه می شود. در مقایسه با روش هایی مانند نیوتن-رافسون که دارای نرخ همگرایی بالاتری هستند، روش تنصیف برای رسیدن به دقت مورد نظر نیاز به تعداد تکرارهای بیشتری دارد.
عدم تأثیر انتخاب مقدار اولیه نزدیک به ریشه
در بسیاری از روش های عددی، انتخاب مقدار اولیه مناسب می تواند باعث کاهش تعداد تکرارها و افزایش سرعت همگرایی شود. اما در روش تنصیف، انتخاب مقدار اولیه نزدیک به ریشه تأثیری در کاهش تعداد تکرارها ندارد، زیرا این روش به جای استفاده از مقدار اولیه خاص، از یک بازه برای محصور کردن ریشه استفاده می کند. به همین دلیل، ممکن است حتی با مقدار اولیه نزدیک به ریشه همچنان نیاز به تعداد زیادی تکرار باشد.
ناتوانی در یافتن ریشه برخی معادلات
روش تنصیف تنها در صورتی قابل استفاده است که بازه اولیه به درستی انتخاب شده و مقادیر تابع در دو انتهای بازه دارای علامت مخالف باشند. برای برخی از معادلات، مانند f(x)=x2f(x) = x^2f(x)=x2، نمی توان بازه ای را یافت که این شرط را برآورده کند، زیرا مقدار تابع در تمام نقاط یک علامت دارد. در چنین مواردی، روش تنصیف قادر به یافتن ریشه نخواهد بود.
نرخ همگرایی خطی
این متد دارای نرخ همگرایی خطی است که باعث کندی روند محاسبات می شود. در روش های عددی، هرچه نرخ همگرایی سریع تر باشد، الگوریتم در زمان کمتری به جواب دقیق نزدیک می شود. روش هایی مانند نیوتن-رافسون دارای نرخ همگرایی درجه دوم هستند که در مقایسه با روش تنصیف بسیار سریع تر عمل می کنند. کند بودن نرخ همگرایی روش تنصیف باعث می شود در مسائل پیچیده، زمان زیادی برای رسیدن به دقت مناسب صرف شود.
عدم توانایی در یافتن ریشه های مختلط
روش تنصیف تنها برای یافتن ریشه های حقیقی کاربرد دارد و نمی تواند ریشه های مختلط را تعیین کند. این به این دلیل است که روش تنصیف بر مبنای تغییر علامت تابع در یک بازه مشخص کار می کند و برای یافتن ریشه های مختلط که در محور حقیقی قرار ندارند، مناسب نیست. در نتیجه، این روش محدود به مسائل خاصی است که ریشه های آنها حتماً در بازه اعداد حقیقی قرار داشته باشند.
عدم کاربرد در بازه های دارای ناپیوستگی
در صورتی که تابع در بازه انتخاب شده ناپیوسته باشد، روش تنصیف قابل استفاده نخواهد بود. این روش به تغییر علامت تابع در یک بازه متکی است، اما اگر در این بازه ناپیوستگی وجود داشته باشد، ممکن است مقدار تابع به طور ناگهانی تغییر کند و شرط محصورسازی به درستی برقرار نباشد. در چنین مواردی، روش های عددی دیگر مانند روش های مبتنی بر مشتق یا تقریب های چندجمله ای مناسب تر خواهند بود.
عدم کاربرد در بازه هایی که مقدار تابع همواره هم علامت است
اگر مقدار تابع در کل بازه دارای یک علامت باشد، روش تنصیف امکان یافتن ریشه را نخواهد داشت. این روش برای کارایی نیازمند یک بازه ای است که در آن مقدار تابع از مثبت به منفی یا برعکس تغییر کند. در غیر این صورت، روش تنصیف نمی تواند تشخیص دهد که ریشه ای درون بازه وجود دارد یا خیر. این محدودیت باعث می شود که روش تنصیف برای بسیاری از انواع معادلات غیرقابل استفاده باشد.
کاربردهای روش تنصیف در متلب
حل معادلات غیرخطی
- یافتن ریشه های معادلات متعالی مانند
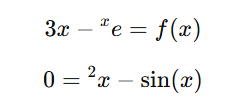
نمونه معادلاتی که روش تنصیف قادر به حل آنها می باشد
- کاربرد در یافتن ریشه های چند جمله ای ها.
مهندسی برق
- تعیین نقاط کاری در تحلیل مدارها.
- حل معادلات پخش بار در سیستم های قدرت.
سیستم های کنترلی
- تعیین حاشیه های پایداری (مانند یافتن قطب های معادله مشخصه).
- استفاده در تحلیل مکان هندسی ریشه ها برای یافتن بهره های بحرانی.
مهندسی مکانیک
- حل معادلات تنش-کرنش در علم مواد.
- تعیین نقاط تعادل در سیستم های دینامیکی.
فیزیک و شیمی
- محاسبه نقاط تعادل در ترمودینامیک و دینامیک سیالات.
- یافتن نقاط بحرانی در تحولات فازی.
مالی و اقتصاد
- یافتن ریشه در مدل های اقتصادی، مانند حل نرخ بهره در معادلات سرمایه گذاری.
- استفاده در مدل های قیمت گذاری اختیار معامله.
مسائل بهینه سازی
- استفاده به عنوان نقطه شروع برای روش های عددی پیشرفتهتر مانند نیوتن-رافسون.
- یافتن نقاط بحرانی در توابع هزینه.
سئو ادیتور2025-12-19T01:08:03+03:30دسامبر 19, 2025|بدون ديدگاه
چکیده مقاله: سئو کلاه خاکستری یکی از تکنیک های بهینه سازی موتور جستجو است که میان سئو کلاه سفید و سئو کلاه سیاه قرار می گیرد. این روش ها معمولاً به استفاده از شیوه [...]
سئو ادیتور2025-12-05T21:34:41+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: در سال ۲۰۲۵ بحث سئو کلاه سیاه دوباره به عنوان يک موضوع جنجالی در حوزه بهينه سازی موتورهای جستجو مطرح شده است. با توجه به به روزرسانی های پي در پی الگوريتم [...]
سئو ادیتور2025-12-05T21:41:27+03:30دسامبر 5, 2025|بدون ديدگاه
چکیده مقاله: بهینه سازی هوش مصنوعی یا AIO به عنوان یکی از پیشرفته ترین رویکردهای دنیای فناوری امروز، بر افزایش کارایی، دقت و سرعت سیستم های هوشمند تمرکز دارد. این مفهوم تنها به بهبود [...]
مدیر2025-12-04T00:29:49+03:30دسامبر 4, 2025|بدون ديدگاه
چکیده مقاله: پرپلکسیتی یک موتور جستجوی هوش مصنوعی است که تلاش می کند جستجو در وب را به شکل هوشمند و پاسخ محور ارائه دهد. این ابزار به جای نمایش فهرست طولانی از لینک [...]
مدیر2025-12-01T00:45:09+03:30دسامبر 1, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های ChatGPT نسل مدل های ChatGPT از نسخه هاي ساده تر مانند GPT-3.5 تا خانواده هاي قدرتمندتر GPT-4 و نسخه هاي بهینه شده آن مانند GPT-4 Turbo و GPT-4o تکامل [...]
مدیر2025-11-28T23:50:42+03:30نوامبر 28, 2025|بدون ديدگاه
چکیده مقاله: انواع مدل های Gemini در سال های اخير به عنوان يکي از پيشرفته ترين خانواده هاي مدل هاي هوش مصنوعي معرفي شده اند و توانسته اند در زمينه هاي مختلف از جمله [...]











