روش نابجایی در متلب: مزایا، معایب و کد نمونه

چکیده مقاله:
روش نابجایی در متلب یا “false position”، یکی از روش های قدیمی برای حل یک معادله با یک مجهول می باشد. به زبان ساده، این روش را می توان به عنوان یک رویکرد آزمون و خطا توصیف کرد که در آن مقادیر “کاذب” یا “آزمایشی” برای متغیر انتخاب شده و سپس این مقدار بر اساس نتیجه به دست آمده تغییر داده می شود. در ادامه، نحوه حل یک معادله یک مجهولی با استفاده از این روش را خواهید آموخت. همچنین، یک مثال از کد نویسی روش نابجایی در متلب، برای فهم بهتر این موضوع برای شما شرح داده شده است.

روش نابجایی در متلب چیست؟

روش نابجایی در متلب به انگلیسی False Position Method in MATLAB یا Regula Falsi Method in MATLAB نامیده می شود.

روش نابجایی یا جابجایی یکی از روش های عددی برای یافتن ریشه های معادلات غیرخطی می باشد. این روش بر پایه تغییر علامت تابع در یک بازه مشخص استوار است. در واقع، اگر یک تابع پیوسته در بازه ای مشخص دارای مقادیر با علامت های متفاوت در دو سر بازه باشد، بر اساس قضیه مقدار میانی حداقل یک ریشه در این بازه وجود دارد. روش نابجایی از این ویژگی استفاده کرده و بازه را به تدریج کوچک تر می کند تا به مقدار تقریبی ریشه نزدیک شود.

• نرم افزار متلب چیست؟

در متلب، این روش با استفاده از یک حلقه تکراری پیاده سازی می شود. ابتدا دو نقطه که تابع در آن ها مقادیر متضاد دارد، انتخاب می شوند. سپس مقدار میانی این دو نقطه محاسبه می شود و بررسی می گردد که آیا مقدار تابع در این نقطه صفر است یا خیر. اگر مقدار تابع در نقطه میانی صفر باشد، این نقطه به عنوان ریشه در نظر گرفته می شود. در غیر این صورت، بازه ای که در آن تغییر علامت رخ داده است، مجددا برای تکرار بعدی در نظر گرفته می شود و این فرآیند تا رسیدن به مقدار تقریبی ریشه ادامه می یابد.

• برنامه نویسی

استفاده از روش نابجایی در متلب به دلیل دقت بالا و همگرایی تضمین شده، در بسیاری از مسائل مهندسی و علمی کاربرد دارد. این روش نسبت به برخی روش های دیگر مانند نیوتن رافسون، از لحاظ پایداری عملکرد بهتری دارد، زیرا وابسته به مشتق تابع نمی باشد. با این حال، سرعت همگرایی آن نسبت به روش های مرتبه بالاتر کمتر است. در متلب می توان با استفاده از یک کد ساده و به کارگیری شرط های توقف مناسب، این روش را به راحتی پیاده سازی کرد.

• مشاوره برنامه نویسی

استنتاج ریاضی روش نابجایی در متلب

یک معادله به صورت f(x)=0 را در نظر بگیرید که فقط شامل یک متغیر، یعنی x، می باشد. برای یافتن ریشه حقیقی این معادله، یک بازه (a, b) را انتخاب می کنیم، به طوری که a<b و f(a) و f(b) دارای علامت های مخالف باشند. بر اساس قضیه مقدار میانی، این شرط تضمین می کند که حداقل یک ریشه بین a و b وجود دارد B[b,f(b)] محور x ها را قطع می کند.

اکنون، معادله خط وتر که نقاط  A[a,f(a)] و  B[b,f(b)] را به هم متصل می کند، به صورت زیر است:

اگر y=0 نقطه تقاطع معادله وتر با محور x  باشد، سپس برای پیدا کردن نقطه تقاطع، معادله  y=0 را در معادله وتر قرار می دهیم.

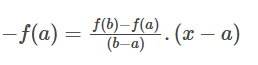
این معادله می‌تواند به صورت زیر ساده‌سازی شود:

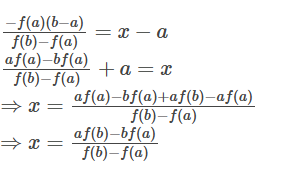
بنابراین، اولین تقریب برای ریشه به صورت x₁ = [af(b) – bf(a)]/ [f(b) – f(a)] می باشد. همچنین، x1 ریشه تابع  f(x1) = 0 است اگر f(x1)=0f(x_1) = 0. اگر  f(x1)≠0 باشد و اگر  f(x1) و  f(a) علامت‌های مخالف داشته باشند، سپس می‌توانیم تقریب دوم را به صورت  x₂ = [af(x₁) – x₁f(a)]/ [f(x₁) – f(a)] بنویسیم. به همین ترتیب، می‌توانیم x3، x4، x5 و غیره را تخمین بزنیم.

• مزایا و معایب زبان برنامه نویسی متلب

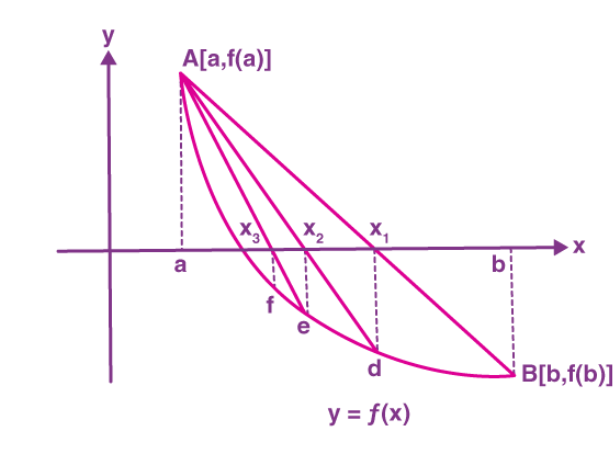
در نمای هندسی، این روش معادله را به صورت نقاط تقاطع نمودار تابع با محور  x نشان می‌دهد. در هر تکرار، یک خط وتر جدید بین نقاط موجود رسم می‌شود که به طور مداوم به ریشه تابع نزدیک ‌تر می‌شود. نقاط تقاطع این وترها با محور  x تقریب‌هایی از ریشه‌های معادله را نمایش می‌دهند.

مزایای استفاده از روش نابجایی در متلب

روش نابجایی یا False Position یکی از روش های عددی برای یافتن ریشه معادلات غیرخطی است. این روش ترکیبی از روش دو بخشی و تقریب خطی است و دارای مزایای متعددی می باشد که در ادامه توضیح داده می شوند.

• روش ژاکوبی در متلب همراه با کد، مزایا و کاربرد

تضمین همگرایی (در صورت انتخاب بازه مناسب)
یکی از مهم ترین ویژگی های روش نابجایی این است که اگر بازه اولیه [a,b] به درستی انتخاب شود، همگرایی به یک ریشه تضمین شده است. شرط لازم برای این تضمین این است که تابع f در دو سر بازه مقادیر مخالف داشته باشد، یعنی f(a)×f(b)<0. این شرط تضمین می کند که حداقل یک ریشه درون بازه قرار دارد و در نتیجه، روش نابجایی به سمت آن همگرا خواهد شد. این خاصیت باعث می شود که این روش نسبت به روش هایی که همگرایی آن ها وابسته به انتخاب اولیه نقاط است، قابل اطمینان تر باشد.

سرعت بیشتر نسبت به روش دو بخشی
روش نابجایی در مقایسه با روش دو بخشی، اغلب دارای همگرایی سریع تری می باشد. در روش دو بخشی، بازه به طور یکنواخت به دو قسمت تقسیم می شود، در حالی که در روش نابجایی از یک تقریب خطی استفاده می شود که وزن بیشتری به نقطه ای که تابع به صفر نزدیک تر است، می دهد. این امر باعث می شود که نقطه جدیدی که به عنوان حدس بعدی انتخاب می شود، نزدیک تر به ریشه واقعی باشد. در نتیجه، تعداد تکرارهای لازم برای رسیدن به دقت مطلوب معمولاً کمتر از روش دو بخشی می باشد.

• شبیه سازی بازوی ربات با متلب

عدم نیاز به مشتق گیری
یکی از مشکلاتی که در برخی روش های یافتن ریشه، مانند روش نیوتن، وجود دارد نیاز به مشتق گیری از تابع می باشد. در حالی که در روش نابجایی، تنها مقادیر تابع در نقاط مشخصی از بازه نیاز است و مشتق گیری از تابع لازم نیست. این ویژگی باعث می شود که روش نابجایی برای توابعی که مشتق گیری از آن ها دشوار است یا مشتق آن ها ناپیوسته می باشد، مناسب باشد. علاوه بر این، در بسیاری از مسائل عملی، به دست آوردن مشتق تابع پیچیده یا غیرممکن است، که روش نابجایی را به یک گزینه کاربردی تبدیل می کند.

دقت بیشتر نسبت به روش دو بخشی در برخی موارد
در برخی شرایط، روش نابجایی می تواند نسبت به روش دو بخشی دقت بیشتری داشته باشد. این موضوع به این دلیل است که در روش نابجایی، نقطه جدید بر اساس مقادیر تابع انتخاب می شود و اگر مقدار تابع در یکی از دو سر بازه به صفر نزدیک باشد، تقریب حاصل دقیق تر خواهد بود. در حالی که روش دو بخشی بدون توجه به مقادیر تابع، بازه را نصف می کند که ممکن است منجر به همگرایی کندتر شود. بنابراین، در شرایطی که مقدار یکی از مقادیر f(a) یا f(b) کوچک باشد، روش نابجایی می تواند نسبت به روش دو بخشی کارایی بالاتری داشته باشد.

سادگی در پیاده سازی
روش نابجایی از نظر پیاده سازی بسیار ساده است. این روش نیازی به محاسبات پیچیده ندارد و تنها شامل چند عملگر ساده جمع، ضرب و تقسیم می باشد. همین ویژگی باعث می شود که بتوان آن را به راحتی در نرم افزارهای عددی مانند متلب پیاده سازی کرد. علاوه بر این، نیازی به استفاده از تکنیک های پیشرفته عددی برای اجرای این روش نیست و حتی افرادی که آشنایی کمی با روش های عددی دارند، می توانند به سادگی آن را پیاده سازی کنند. این سادگی، همراه با دقت مناسب و تضمین همگرایی، باعث شده است که روش نابجایی یکی از گزینه های محبوب برای یافتن ریشه معادلات باشد.

• مقایسه متلب با پایتون

معایب استفاده از روش نابجایی در متلب

روش نابجایی با وجود مزایای زیادی که دارد، دارای برخی معایب نیز می باشد که در برخی شرایط می تواند باعث کاهش کارایی آن شود. این معایب به خصوص در مقایسه با روش های دیگر مانند روش نیوتن یا روش مماس (Secant Method) بیشتر نمایان می شوند. در ادامه، مهم ترین معایب این روش توضیح داده می شوند.

• شبیه سازی با متلب

همگرایی کند در برخی موارد
یکی از مشکلات اصلی روش نابجایی این است که در برخی موارد می تواند به کندی همگرا شود. اگر مقدار تابع در یکی از دو سر بازه از نظر قدر مطلق بسیار کوچک باشد، نقطه انتهایی بازه ممکن است برای مدت زیادی ثابت بماند و تنها یک سمت بازه به روز رسانی شود. این موضوع باعث می شود که سرعت همگرایی کاهش پیدا کند و فرآیند یافتن ریشه زمان بیشتری ببرد. در مقابل، روش مماس هر دو نقطه را به روز رسانی می کند که معمولاً منجر به همگرایی سریع تر می شود. بنابراین، در مواردی که روش نابجایی دارای همگرایی کند است، ممکن است روش های جایگزین عملکرد بهتری داشته باشند.

ناموفق در برخی توابع
روش نابجایی برای برخی از توابع به درستی عمل نمی کند یا ممکن است به کندی همگرا شود. به عنوان مثال، اگر تابع دارای چندین ریشه باشد، ممکن است این روش به جای یافتن ریشه مورد نظر، به سمت یک ریشه دیگر همگرا شود. همچنین، اگر تابع در نقطه ای دارای مماس افقی باشد، مانند تابع f(x) = x³ در نزدیکی صفر، روش نابجایی ممکن است متوقف شده یا به کندی همگرا شود. دلیل این موضوع آن است که روش نابجایی از خط واصل بین دو نقطه استفاده می کند و اگر این خط تقریب مناسبی از رفتار تابع در ناحیه مورد نظر ارائه ندهد، ممکن است الگوریتم به درستی عمل نکند.

• کاربرد متلب در ریاضیات

نیاز به یک بازه حاوی ریشه
یکی دیگر از محدودیت های روش نابجایی این است که تنها زمانی قابل استفاده است که بازه اولیه [a,b] شامل حداقل یک ریشه باشد. به عبارت دیگر، باید شرط f(a)×f(b)<0 برقرار باشد تا روش بتواند اجرا شود. اگر بازه ای انتخاب شود که این شرط را نداشته باشد، روش نابجایی شکست خواهد خورد و هیچ نتیجه ای ارائه نخواهد داد. این موضوع باعث می شود که انتخاب بازه اولیه نقش بسیار مهمی در موفقیت این روش داشته باشد و در برخی موارد نیاز به آزمایش های اضافی برای تعیین یک بازه مناسب باشد.

عدم داشتن همگرایی درجه دوم
یکی از دلایلی که روش نابجایی در برخی موارد کندتر از روش های دیگر است، این است که برخلاف روش نیوتن، دارای همگرایی درجه دوم نمی باشد. در روش نیوتن، سرعت همگرایی در مراحل بعدی افزایش پیدا می کند که باعث می شود ریشه با تعداد تکرارهای کمتر و دقت بالاتر به دست آید. اما در روش نابجایی، همگرایی معمولاً خطی است، به این معنی که مقدار تقریب ریشه در هر مرحله تغییرات کمتری دارد و رسیدن به دقت های بسیار بالا ممکن است زمان زیادی ببرد. این ویژگی باعث می شود که در مسائلی که نیاز به دقت بالا دارند، روش نیوتن گزینه بهتری نسبت به روش نابجایی باشد.

• شبیه سازی

مثال کد روش نابجایی در متلب

در ادامه به بررسی مثالی خواهیم پرداخت که استفاده از روش نابجایی در متلب ، برای یافتن ریشه های معادله x3 – x2 – 2=F(x) کد نویسی می کند و با استفاده از روش (False Position)، ریشه آن را در بازه [1,2] تا رسیدن به دقت مشخص شده (10^(-6)) یا حداکثر 50 تکرار محاسبه می کند.

کاربرد های روش نابجایی در متلب

روش نابجایی یکی از روش های پرکاربرد در متلب برای یافتن ریشه های معادلات غیرخطی است. این روش به دلیل دقت مناسب، سادگی پیاده سازی و عدم نیاز به مشتق گیری، در حوزه های مختلف علمی و مهندسی مورد استفاده قرار می گیرد. در ادامه، برخی از کاربردهای مهم این روش ارائه شده اند.

یافتن ریشه ها در مسائل مهندسی

در مهندسی، بسیاری از مسائل شامل توابع غیرخطی هستند که رفتار پدیده های فیزیکی را مدل سازی می کنند. این توابع ممکن است مرتبط با تحلیل تنش، انتقال حرارت، جریان سیالات و دیگر فرآیندهای فیزیکی باشند. یافتن ریشه این توابع می تواند به تعیین نقاط تعادل، نقاط بحرانی و شرایط شکست کمک کند. به عنوان مثال، در تحلیل ساختاری، این روش می تواند برای یافتن نیرویی که باعث تسلیم شدن یک ماده می شود، استفاده شود. همچنین، در تحلیل حرارتی، می توان از این روش برای یافتن دمایی که در آن دو ماده به تعادل حرارتی می رسند، بهره برد.

مثال‌ها:

• تحلیل ساختاری: پیدا کردن بار در نقطه ‌ای که یک ماده به نقطه تسلیم خود می ‌رسد.
• تحلیل حرارتی: پیدا کردن دمایی که دو ماده به تعادل حرارتی می‌ رسند.

مسائل بهینه سازی

روش نابجایی در بسیاری از مسائل بهینه سازی به کار می رود، به ویژه در مواردی که مشتق گیری از تابع مشکل باشد. در بسیاری از الگوریتم های بهینه سازی، نیاز به یافتن نقاطی وجود دارد که در آن ها مقدار تابع به حداقل یا حداکثر برسد. یکی از کاربردهای مهم این روش در یادگیری ماشین است، جایی که برای یافتن مقادیر بهینه تابع هزینه استفاده می شود. در این حالت، هدف کاهش مقدار خطا یا زیان در یک مدل یادگیری ماشین است که روش نابجایی می تواند به یافتن این مقدار کمک کند.

مثال:

• در کمینه ‌سازی تابع هزینه در یادگیری ماشین(machine learning) ، روش false position می ‌تواند برای یافتن مقادیری که خطا یا زیان را حداقل می‌کنند، استفاده شود.

تحلیل مدارهای الکتریکی

در مهندسی برق، بسیاری از مسائل شامل یافتن نقاطی است که در آن ها ولتاژ یا جریان به یک مقدار مشخص می رسد. روش نابجایی می تواند برای حل معادلاتی که مشخصه های مدارهای الکتریکی را توصیف می کنند، مورد استفاده قرار گیرد. به عنوان مثال، در تحلیل مدارهای AC، ممکن است نیاز باشد فرکانسی که در آن امپدانس مدار صفر می شود، محاسبه شود. همچنین، در طراحی فیلترهای الکترونیکی، این روش می تواند برای یافتن مقادیر بهینه اجزای مدار به کار رود.

• روش وتری در متلب

مدل سازی فرآیندهای شیمیایی

در مهندسی شیمی، بسیاری از واکنش ها و فرآیندهای صنعتی با استفاده از معادلات غیرخطی مدل سازی می شوند. روش نابجایی می تواند برای یافتن شرایطی که در آن ها واکنش به تعادل می رسد یا یک خاصیت فیزیکی خاص مانند فشار یا دما به مقدار مشخصی می رسد، مورد استفاده قرار گیرد. به عنوان مثال، در محاسبه نقطه جوش یک ماده در فشارهای مختلف، این روش می تواند به یافتن دمایی که در آن فشار بخار برابر با فشار محیط است، کمک کند.

تحلیل دینامیک سیالات

در مسائل مرتبط با دینامیک سیالات، یافتن مقادیر خاصی مانند سرعت جریان، فشار بحرانی و ضریب اصطکاک بسیار اهمیت دارد. روش نابجایی می تواند برای حل معادلاتی که مشخصات جریان سیال را توصیف می کنند، استفاده شود. به عنوان مثال، در تحلیل جریان در لوله ها، این روش می تواند برای یافتن نقطه ای که در آن سرعت جریان تغییر ناگهانی دارد یا افت فشار قابل توجهی رخ می دهد، به کار رود. همچنین، در طراحی سیستم های تهویه، می توان از این روش برای تعیین شرایطی که در آن ها جریان هوا به تعادل می رسد، استفاده کرد.

حل معادلات اقتصادی و مالی

در اقتصاد و امور مالی، بسیاری از مدل ها شامل معادلات غیرخطی هستند که تعیین مقادیر بهینه را دشوار می کنند. روش نابجایی می تواند برای حل معادلاتی که قیمت تعادلی، نرخ بهره مناسب یا نقطه سربه‌سر را مشخص می کنند، مورد استفاده قرار گیرد. به عنوان مثال، در تحلیل حساسیت یک سرمایه گذاری، می توان از این روش برای یافتن نرخ بازده داخلی (IRR) استفاده کرد. همچنین، در مدل های اقتصادی که عرضه و تقاضا را توصیف می کنند، روش نابجایی می تواند برای یافتن نقطه ای که در آن بازار به تعادل می رسد، به کار رود.